压缩传感技术在小动物自门控心脏电影序列中的应用（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

目的

理论与方法

结果

结论

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、数据、文献

---

💥1 概述

文献来源：

目的

在临床前应用中，自门控电影序列是心脏 MRI 的常见选择。我们的工作目的是将压缩传感技术应用于大鼠的IntraGateFLASH心脏MRI研究，并找到该技术可实现的最大加速因子。

理论与方法

我们的重建方法扩展了Split Bregman公式，以最小化空间和时间的总变化。此外，我们分析了欠采样模式对可实现的加速因子的影响。

结果

我们的结果表明，当使用适当的欠采样模式时，我们的技术可以实现高达 15 的加速因子。时变随机抽样的引入明显提高了欠采样方案的效率。在计算效率方面，与文献中发现的最快方法相比，所提出的重建方法已被证明具有竞争力。

结论

我们成功地将我们的压缩传感技术应用于小动物的自门控心脏电影采集，获得了高达15的加速因子，几乎不明显的图像退化。

在临床和临床前应用中，不同类型的心脏电影序列被广泛用于评估心脏功能、评估心脏动力和量化射血分数。其中一些电影序列可以使用前瞻性或回顾性门控。在前瞻门控中，心电图 （ECG） 信号用于将图像采集与心动周期同步，而呼吸信号则用于通过在呼吸周期的特定时刻中断采集来避免运动伪影。前瞻性门控的一个缺点是，在高视场下使用电极具有挑战性，并且容易产生伪影，尤其是在小动物研究中。回顾性心脏门控通过连续采集消除了对心电图的需求，该采集根据导航器回波回顾性地分类为不同的心脏阶段，从而可以生成心脏和呼吸同步信号。IntraGateFLASH 1 是一种自门控 FLASH（快速低角度拍摄），是自门控快速梯度回波序列的一个示例，其中导航器回波与每条相位编码线一起存储。根据其对应的导航器信号，对不同的相位编码进行回顾性排序和平均，以排列几个完整的k空间（图1）。1）.

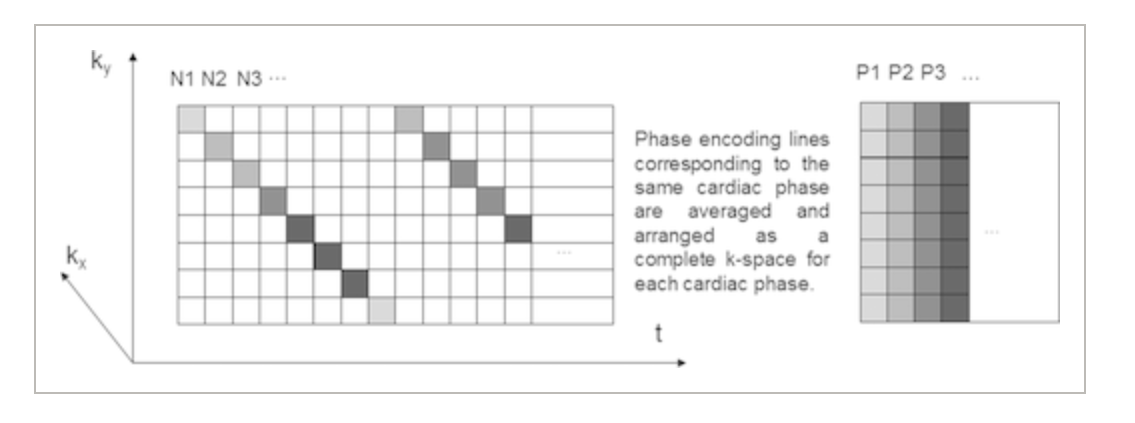
在心血管应用中，采集时间与重建图像的时空分辨率和信噪比（SNR）直接相关。有几种加速方法可以实现更快的采集（或更高质量的图像，如果保持采集时间）。在过去的几年中，使用 UNFOLD 2、k-t BLAST 和 k-t SENSE 3、PARADIGM 4、k-t SPARSE 5、k-t FOCUSS 6、k-t PCA 7、基于 PSF 模型的重建 8-10、k-t ISD 11 和 k-t SLR 12 等方法报告了心脏 MRI 的良好结果。还报道了许多其他方法13-19。

压缩传感（CS）范式指出，如果我们可以假设图像在像素空间或任何其他变换域20,21中具有稀疏表示，则可以使用适当的非线性方法从随机欠采样数据中实现精确的图像重建。重建的质量取决于数据欠采样的程度和图像稀疏性，以及所使用的特定非线性重建算法22。

就其空间表示而言，某些图像实际上可能是稀疏的，就像血管造影研究中的情况一样。在其他情况下，最常见的方法是使用图像渐变作为转换域。如果存在稀疏解，则可以通过最小化图像梯度的 L1 范数（也称为全变异 （TV））来找到它。在动态应用中（涉及时间维度），我们可以利用空间和时间稀疏性，因为连续采集的图像有望显示出很强的相关性。因此，正如我们在这项工作中提出的那样，可以在空间和时间维度上最小化电视。

对于动态应用，CS问题的规模可能会大大增加，并且需要计算密集型计算。在可用的各种重建算法中，Split Bregman 方法和类似的过程 23-26 已被证明在解决 L1 泛函问题方面比经典优化方法更具计算效率，尤其是在空间电视最小化方面。尽管 Split Bregman 方法已经成功应用于静态 MRI 图像 27-30，但时空方法的潜在优势尚未得到评估。

以前大多数用于人类心脏 MRI 的动态 CS 方法都集中在前瞻性电影采集上;只有两项纳入了回顾性分类6、19。关于小动物临床前应用的先前工作很少 9、16、31-33，只有最近的一项研究涉及回顾性自门控电影序列 33 的使用。

 详细文章讲解见第4部分。

📚2 运行结果

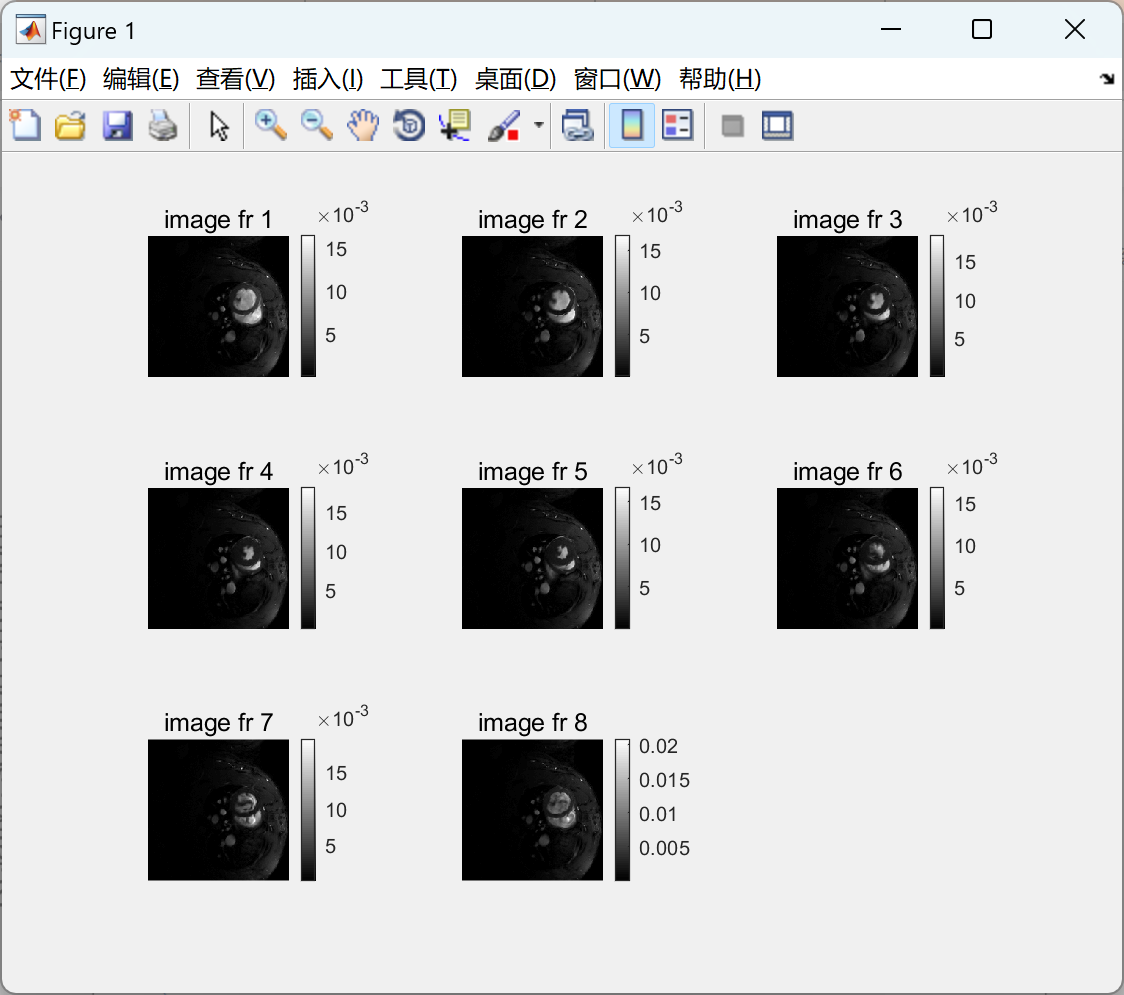
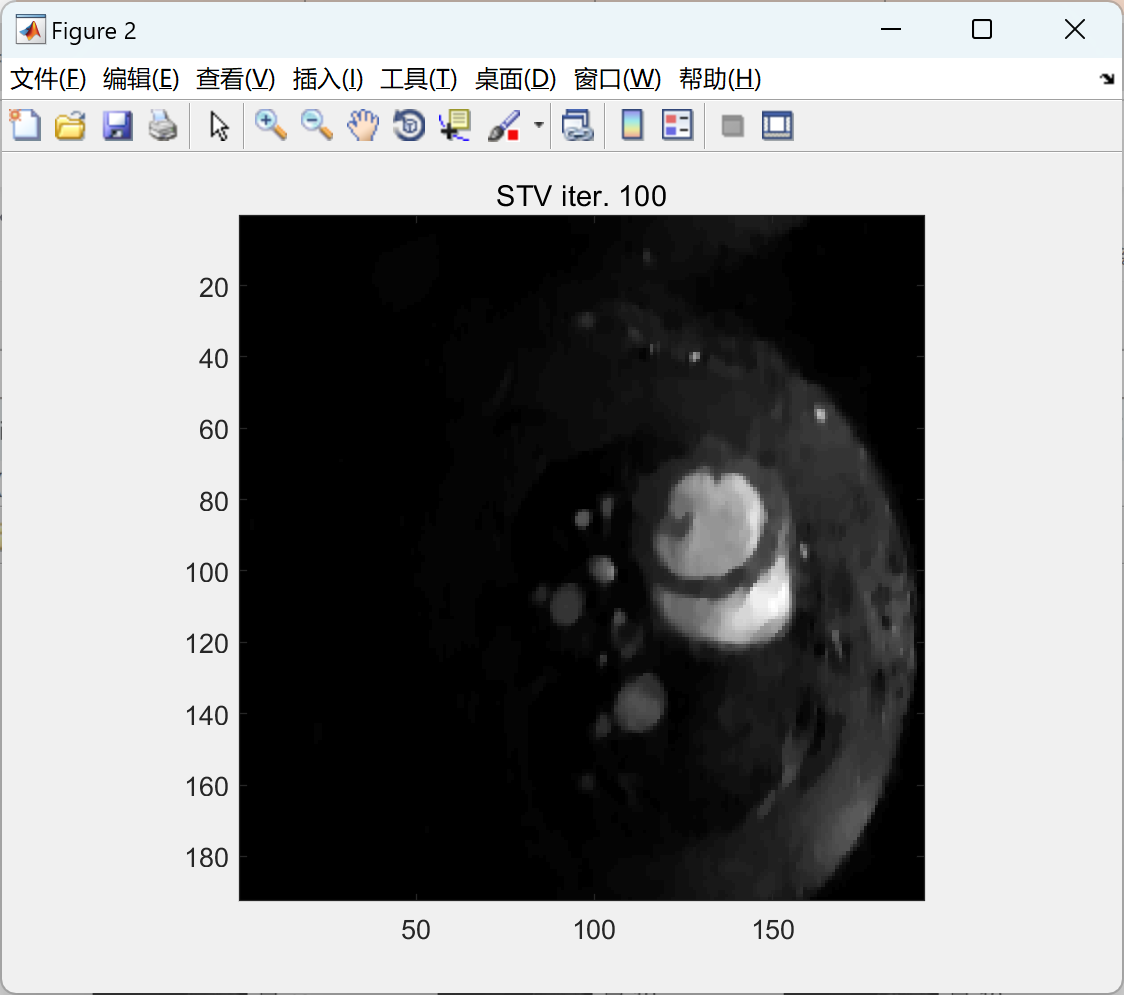
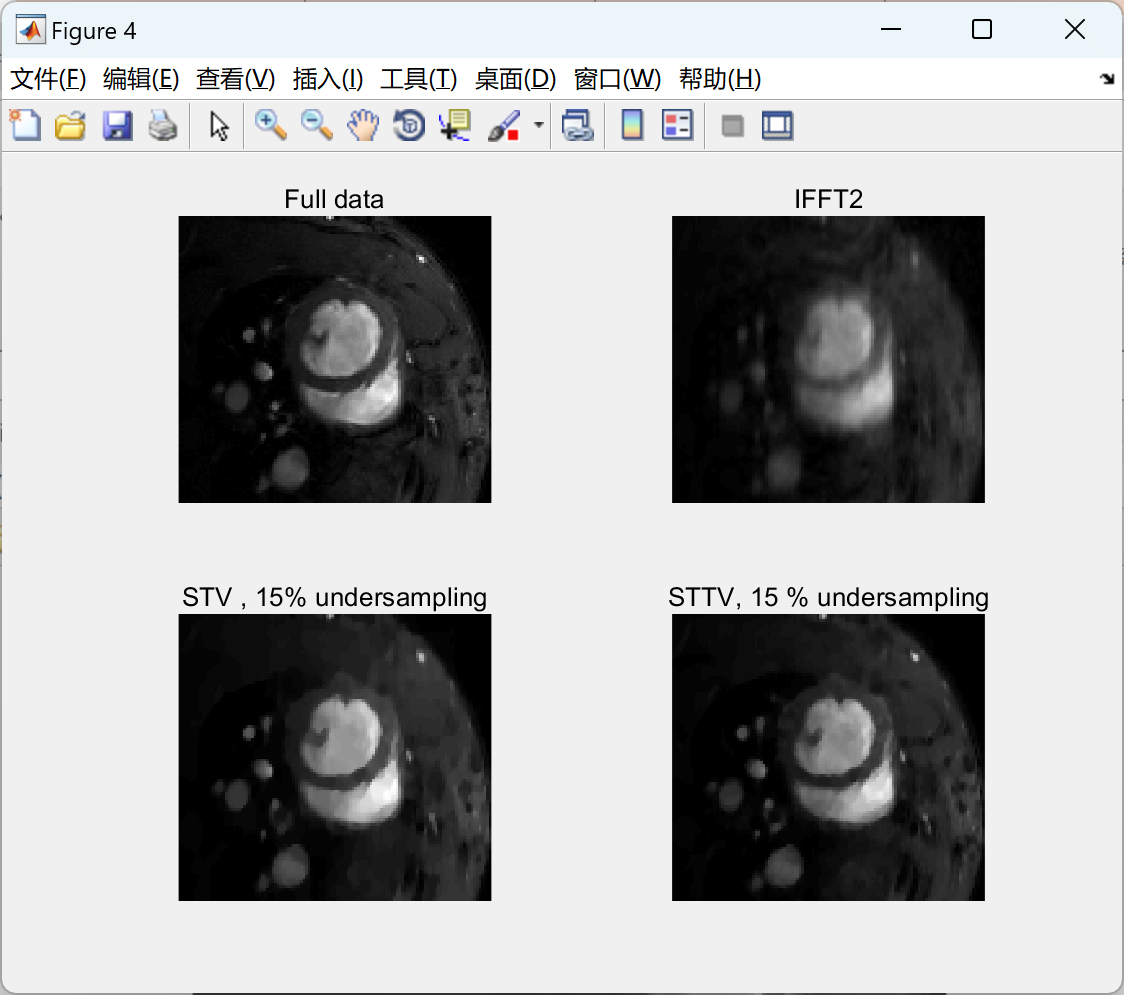
部分代码：

% Goldstein's spatial TV using the Split Bregman formulation
% u_tv = mrics(RAll(:,:,1),data(:,:,1), mu, lambda, gamma, nInner, nBreg);
% 
% SpatialTVSB.m: same as mrics.m but it computes the solution error
% norm
% Reconstruction of one slice only
[u_tv,err_tv] = SpatialTVSB(RAll(:,:,fr),data(:,:,fr), mu, lambda, gamma, nInner, nBreg,image0(:,:,fr));
% ------------------------------------------------------------------------
% SpatioTemporal Total Variation with larger temporal sparsity
% Dynamic reconstruction
betaxy      = 0.3;
betat       = 0.7;
mu          = 1;
lambda      = 1;
gamma       = 1;
nInner      = 1;
nBreg       = 100;
[u_ttv,err_ttv] = SpatioTemporalTVSB(RAll,data,N,betaxy,betat,mu,lambda,gamma,nInner,nBreg,image0);
% ------------------------------------------------------------------------
% Comparison of results
figure; 
tmp     = (image0(:,:,fr));
subplot(2,2,1); imagesc(abs(tmp(40:150,70:190))); axis image; 
axis off; colormap gray; title('Full data'); ca = caxis;
tmp     = (u_ifft);
subplot(2,2,2); imagesc(abs(tmp(40:150,70:190))); axis image; 
axis off; colormap gray; title('IFFT2'); caxis(ca);
tmp     = (u_tv);
subplot(2,2,3); imagesc(abs(tmp(40:150,70:190))); axis image; 
axis off; colormap gray; title(['STV , ' num2str(100*sparsity) '% undersampling' ]);
tmp     = (u_ttv(:,:,fr));
subplot(2,2,4); imagesc(abs(tmp(40:150,70:190))); axis image; 
axis off; colormap gray; title(['STTV, ' num2str(100*sparsity) ' % undersampling' ]);
caxis(ca);
drawnow; 

% Minimum error norm
norm(u_tv(:)-reshape(image0(:,:,fr),[],1))/norm(reshape(image0(:,:,fr),[],1))
norm(reshape(u_ttv(:,:,fr),[],1)-reshape(image0(:,:,fr),[],1))/norm(reshape(image0(:,:,fr),[],1))

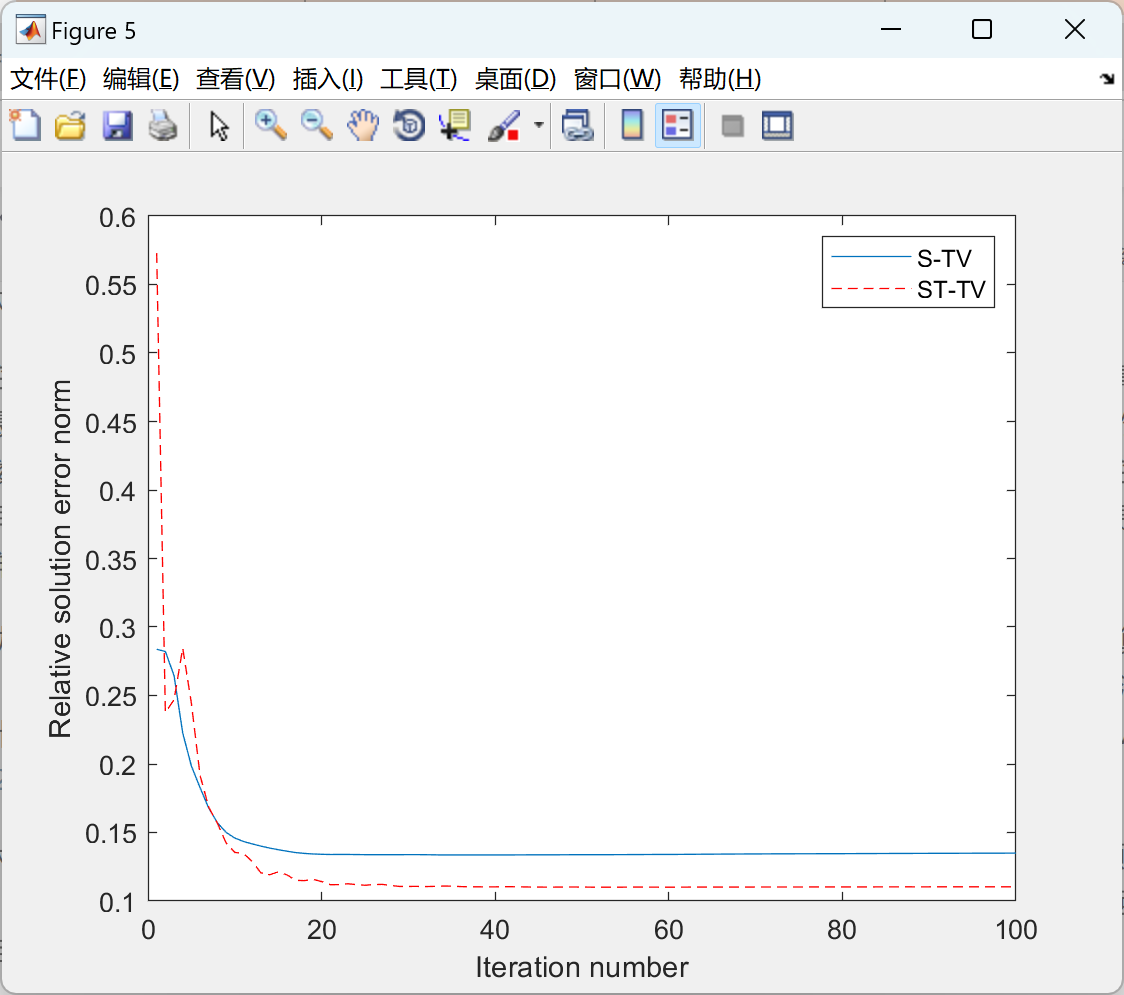
% Convergence
figure, plot(err_tv); hold on; plot(err_ttv(:,fr),'--r'); 
xlabel('Iteration number'); ylabel('Relative solution error norm'); 
legend('S-TV','ST-TV');

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

🌈4 Matlab代码、数据、文献