【非线性多轴恒定延性谱】生成多分量恒定延展性非线性非弹性响应谱的鲁棒功能研究（Matlab代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

本文介绍了一种非线性多轴恒定延性谱方法，它可以生成多组分恒定延展性非线性非弹性响应谱，适用于多轴同时激励，包括水平、垂直和旋转运动（即旋转加速度和倾斜）。此外，它还可以计算传递给SDOF振荡器的地震输入能量的分量。

这种鲁棒功能的特点在于支持多轴激励（同时进行水平、垂直和旋转输入地震动）和材料非线性由Ozdemir的速率无关力-位移模型表示。该模型可以预测不同振动级别下的结构和地基反应。此外，该方法还包括P-delta（全局水平）和恒定屈服位移的光谱分析。这使得用户可以更加精细地控制预测结果，并对振动输入的参数进行准确描述。

在该方法中，输入能量的绝对能量和相对能量分量的计算和输出结果是特别重要的功能。这可以帮助用户更好地进行结构分析和系统优化。同时，输出结果也可用于评估和验证该模型的性能和准确性，进而指导结构的设计和改进。

最后，本文以输入Pacoima大坝的地震动来验证该模型的实际运用价值。该模型能够准确预测建筑物及其基础在地震激励下的反应，进而为地震安全工程提供了重要的支撑。

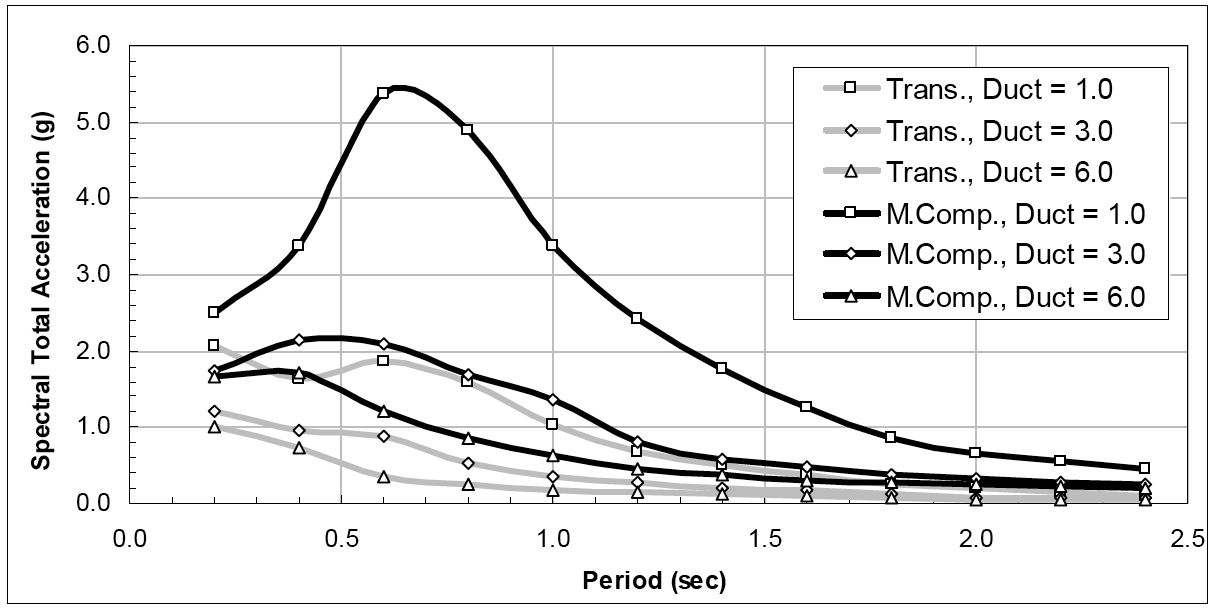
📚2 运行结果

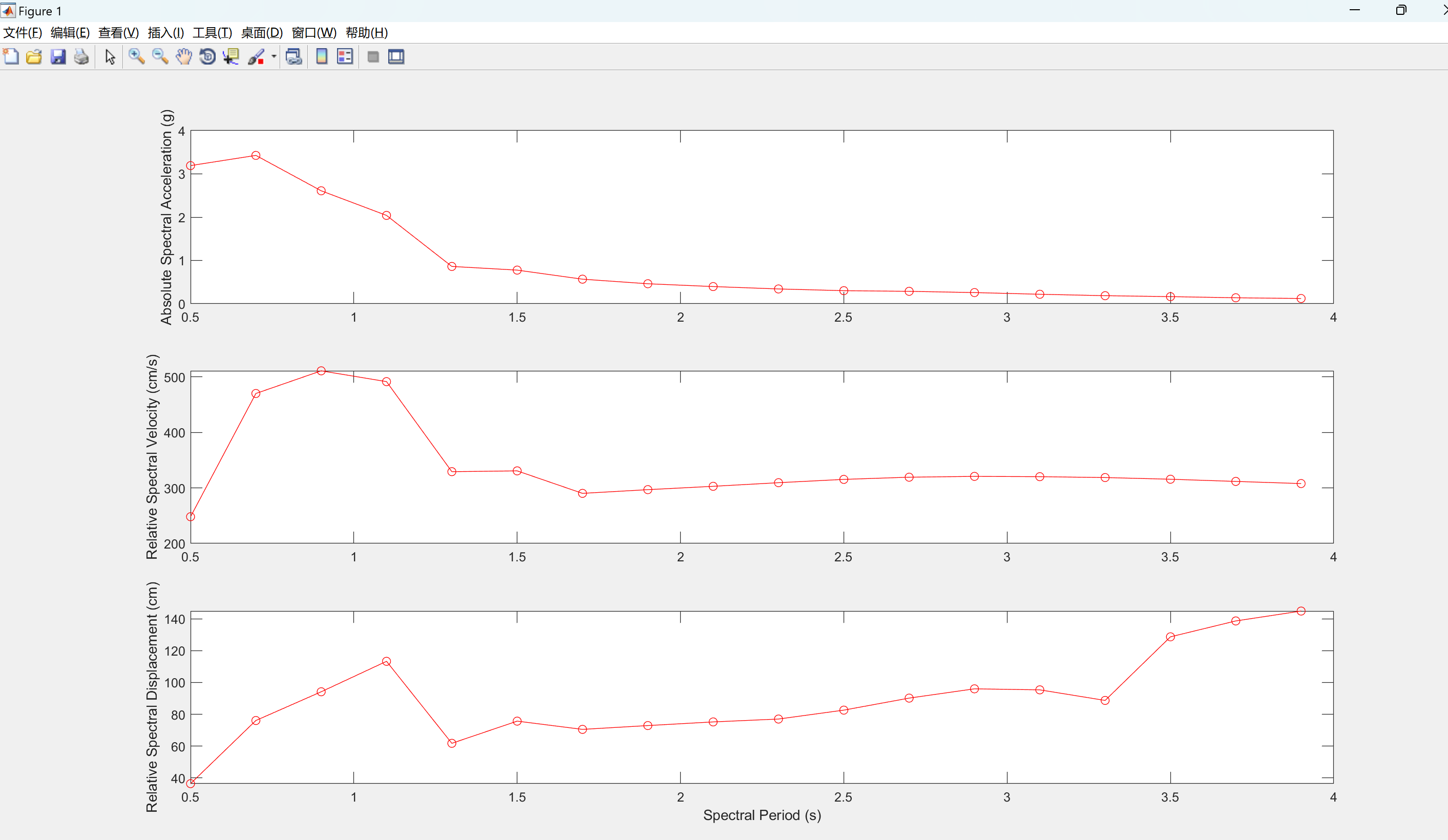
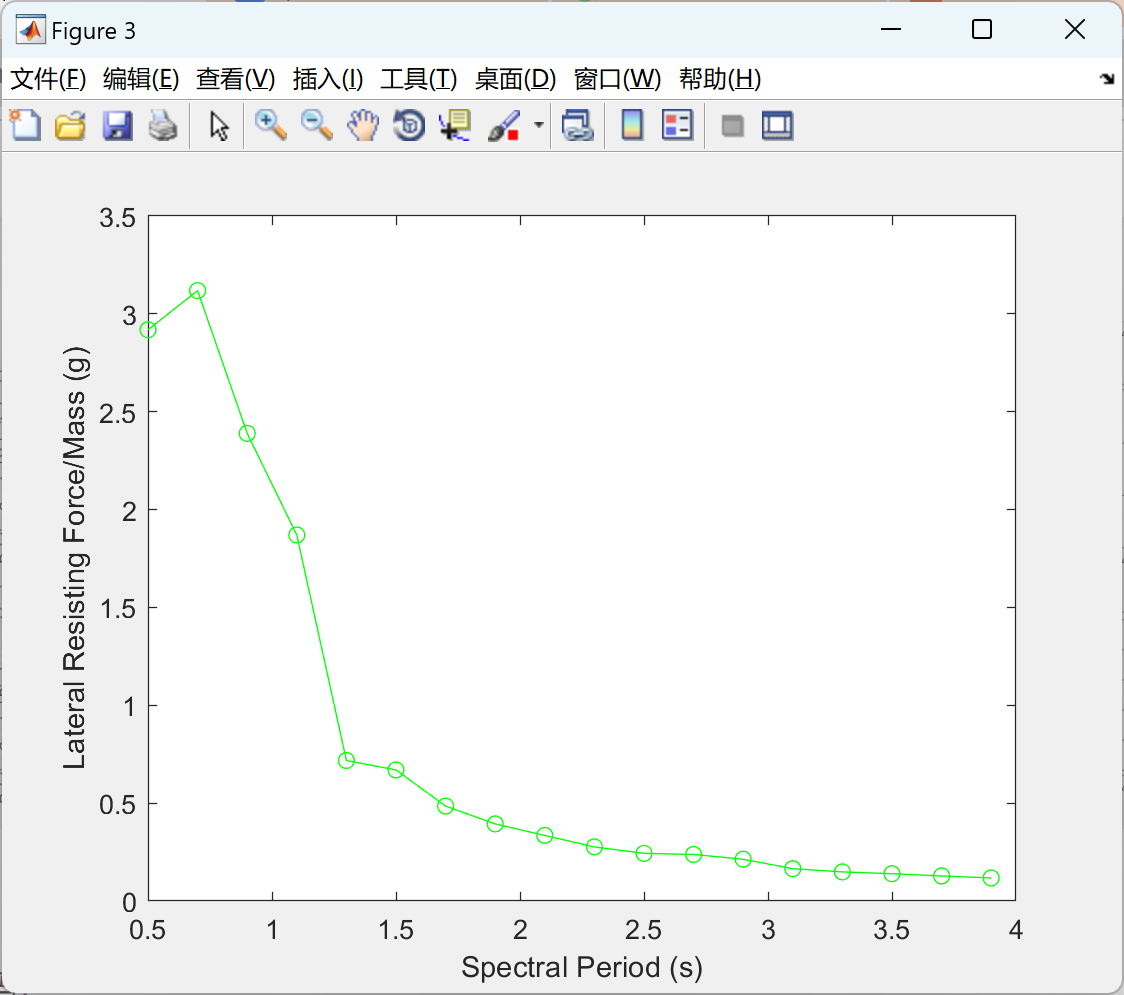
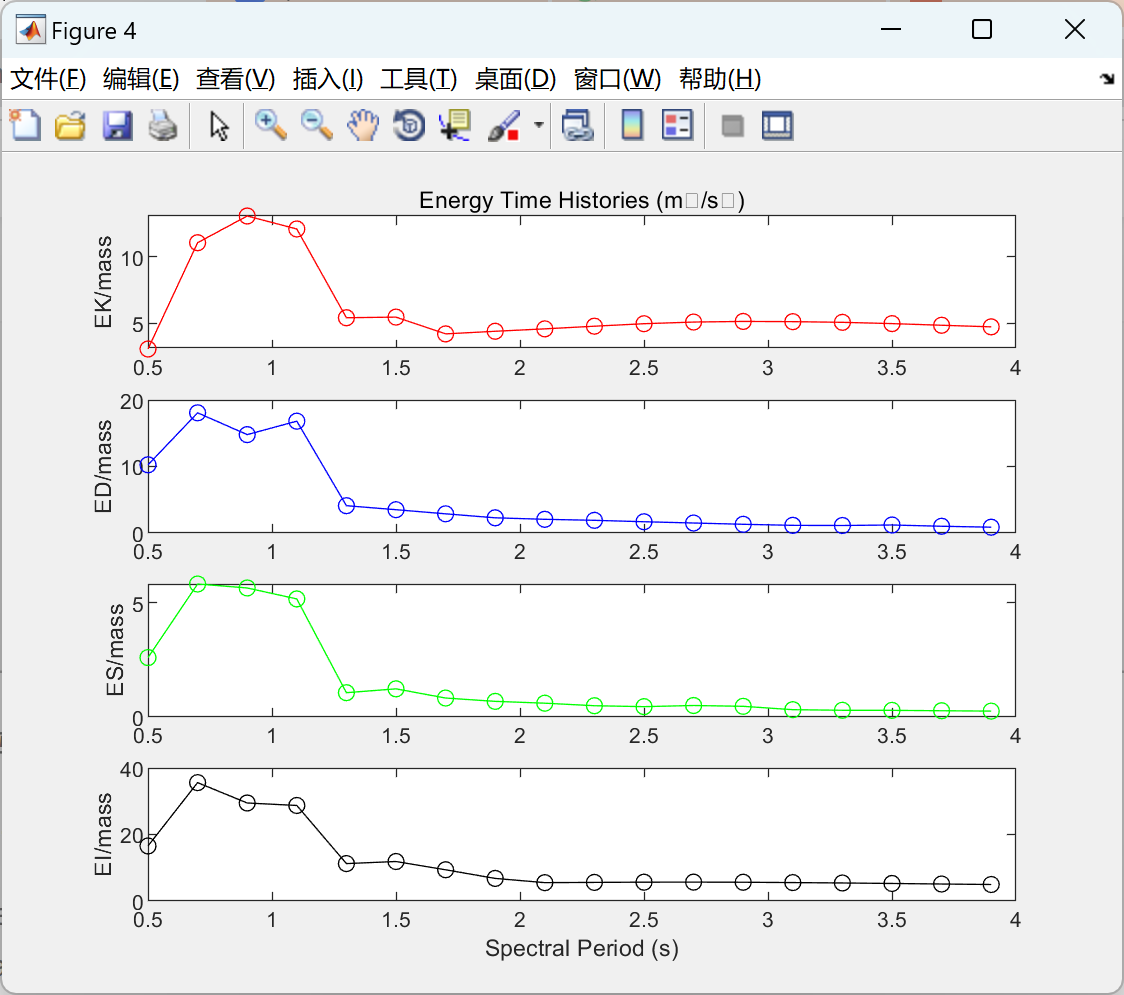
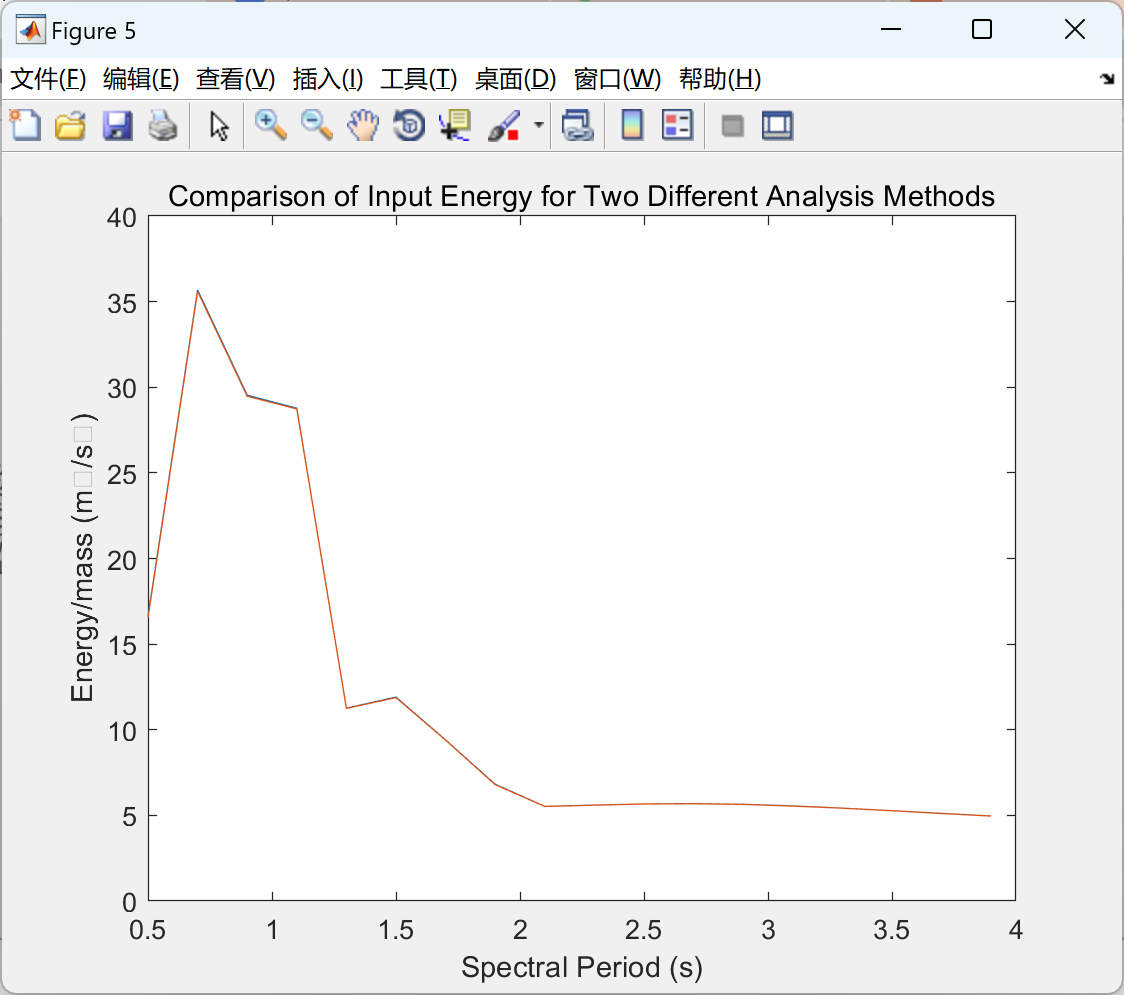
主函数代码：

clear; close all; clc;

% Call spectra input data function
[Ti,Tf,deltaT,xi,g,l,sPeriod,tgt] = spectraInput;

% Call ground motion input data function
[gacc, gaccZ, N, dt, td, tspan] = groundMotionData(l,g);

% Call material input data function
[fy,alpha,eta] = materialInput;

% Assign values to oscillator properties
Kg = g/l;          
% Geometric stiffness term (1/s)
Tg = 2*pi*(1/Kg)^.5; % Geometric oscillation period (s) see ASCE paper by Kalkan & Graizer (2007)
fprintf('Tg = %3.2f, Target Ductility %3.2f\n',Tg,tgt)

% Assign values to integration variables
for i = 1:length(sPeriod);  % Loop over spectral periods
    y1o = 0;             % Initial value of y1
    y2o = 0;             % Initial value of y2
    y3o = 0;             % Initial value of y3
    y4o = 0;             % Initial value of y4
    y5o = 0;             % Initial value of y5
    yo = [y1o;y2o;y3o;y4o;y5o];  % Initial conditions for state vector
    
    Tn = sPeriod(i);        % Natural period (s)
    fprintf('\n Spectra for %3.2f damping is computed for %3.2f (s)\n',xi,Tn)
    omegan = 2*pi/Tn;       % Natural frequency (rad/s)
    
    % Call solver and iteration routine
    SDOF
    
    % Call post processing file
    [absacc, Ekoverm, Edi, Edoverm, Ehi, Ehoverm, Esoverm, Eyoverm, Eii, Eioverm, Eioverm2] = processResults(gacc,omegan,veloc,foverm,tspan,xi);
    
    % Extract spectral values
    processSpectra
end
save ../out/spectra.mat

% Call plotting file
plotResultsSpectra;

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]刘鹏飞,杨文国.对鲁棒线性规划保守性的进一步讨论[J].中国科学院研究生院学报, 2015(005):032.

[2]  Kalkan, E. and Graizer V. (2007). "Coupled Tilt and Translational
  Ground Motion Response Spectra", ASCE Journal of Structural
  Engineering, 133(5): 609-619, 2007.

[3]  Kalkan, E. and Kunnath, S.K. (2008). ?Relevance of Absolute and
  Relative Energy Content in Seismic Evaluation of Structures?, Advances
  in Structural Engineering, 11(1): 17-34.

🌈4 Matlab代码实现