✅作者简介:热爱科研的Matlab仿真开发者,擅长数据处理、建模仿真、程序设计、期刊写作与指导,代码获取、论文复现及科研仿真合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
🔥内容介绍
多变量回归预测在诸多领域,例如金融预测、气象预报和医学诊断等,都扮演着至关重要的角色。传统的多变量回归模型,例如线性回归和岭回归,往往受限于其对数据线性关系的假设,难以有效捕捉复杂非线性关系。近年来,支持向量机(SVM)和Transformer模型在处理非线性数据方面展现出强大的能力,将两者结合用于多变量回归预测,成为一个值得深入研究的方向。本文将探讨SVM-Transformer融合方法在多变量回归预测中的应用,分析其优势和挑战,并展望未来的研究方向。
一、 支持向量机(SVM)在回归预测中的应用
支持向量机最初被提出用于分类问题,其核心思想是寻找最大间隔超平面,将不同类别的样本有效分离。在回归问题中,SVM通过引入松弛变量和损失函数,寻找一个最佳拟合超平面,以最小化预测值与真实值之间的偏差。支持向量回归(SVR)是SVM在回归问题中的应用,它能够处理高维数据和非线性关系,具有较好的泛化能力。然而,SVR的性能受核函数选择和参数调优的影响较大,且在处理大规模数据集时计算效率相对较低。
二、 Transformer模型在回归预测中的应用
Transformer模型最初在自然语言处理领域取得了显著成功,其核心在于自注意力机制(Self-Attention)。自注意力机制能够捕捉数据中不同部分之间的长程依赖关系,这使得Transformer模型能够有效处理序列数据和高维特征。通过堆叠多个Transformer编码器层,可以构建更深层次的模型,从而提高模型的表达能力和预测精度。将Transformer应用于回归预测,需要对其进行适当的修改,例如调整输出层以适应回归任务的要求,并选择合适的损失函数进行优化。Transformer模型在处理大规模数据集方面具有优势,但其参数数量巨大,容易出现过拟合现象,需要进行有效的正则化处理。
三、 SVM-Transformer融合方法的探索
结合SVM和Transformer的优势,可以构建一种新型的多变量回归预测模型。一种可能的融合方法是将Transformer作为特征提取器,将原始数据输入Transformer模型,学习其深层特征表示,然后将提取到的特征作为SVM模型的输入,进行最终的回归预测。这种方法利用Transformer强大的特征提取能力,能够有效捕捉数据中的复杂非线性关系,同时利用SVM模型的优势,进行高效的回归预测。
另一种融合方法是将SVM与Transformer进行并行处理,分别对数据进行建模,然后对两个模型的预测结果进行融合。例如,可以利用加权平均或者投票机制等方法对不同模型的预测结果进行整合,以提高预测的准确性和稳定性。这种方法可以有效利用两种模型的优势,并降低单一模型的风险。
四、 优势与挑战
SVM-Transformer融合方法相比于传统的回归模型,具有以下优势:
- 强大的非线性建模能力:
Transformer能够有效捕捉数据中的长程依赖关系和复杂非线性关系,而SVM也具有处理非线性数据的能力。
- 高效的特征提取:
Transformer能够学习到更有区分度的特征,提高模型的预测精度。
- 较好的泛化能力:
合适的正则化策略能够有效避免过拟合,提高模型的泛化能力。
然而,这种融合方法也面临一些挑战:
- 参数调优难度:
SVM和Transformer模型都包含大量的参数,需要进行精细的调优,才能取得最佳的预测效果。
- 计算复杂度:
Transformer模型的参数量巨大,计算复杂度较高,需要强大的计算资源。
- 可解释性:
深度学习模型的可解释性较差,难以理解模型的预测机制。
五、 未来研究方向
未来研究可以集中在以下几个方面:
- 改进融合策略:
探索更有效的SVM-Transformer融合策略,例如采用多层级融合或者级联结构。
- 优化参数调优方法:
研究高效的参数调优方法,例如贝叶斯优化或遗传算法,以提高模型的性能。
- 提高模型的可解释性:
研究提高模型可解释性的方法,例如采用注意力机制的可视化技术或特征重要性分析方法。
- 探索不同类型的Transformer模型:
探索不同类型的Transformer模型,例如轻量级Transformer或针对特定任务优化的Transformer模型,以提高模型的效率和性能。
- 应用于不同领域的数据集:
将SVM-Transformer模型应用于不同领域的数据集,验证其泛化能力和适用性。
六、 结论
SVM-Transformer融合方法为多变量回归预测提供了一种新的思路,其强大的非线性建模能力和高效的特征提取能力能够显著提高预测精度。尽管面临一些挑战,但通过持续的研究和改进,该方法有望在诸多领域取得更广泛的应用,推动多变量回归预测技术的进步。 未来的研究应该集中在优化模型结构、提高模型效率和增强模型可解释性等方面,以实现更精准、高效和可靠的多变量回归预测。
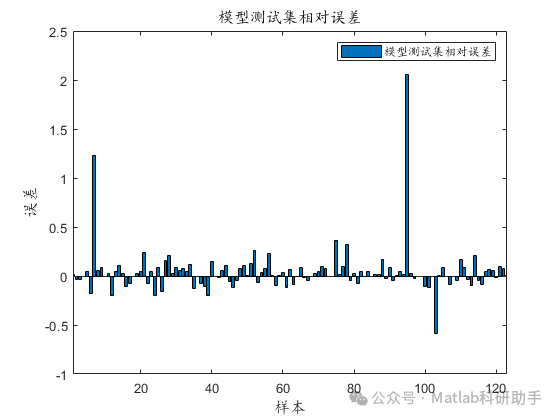
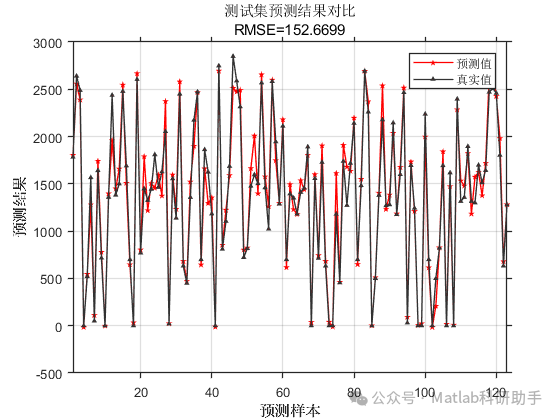
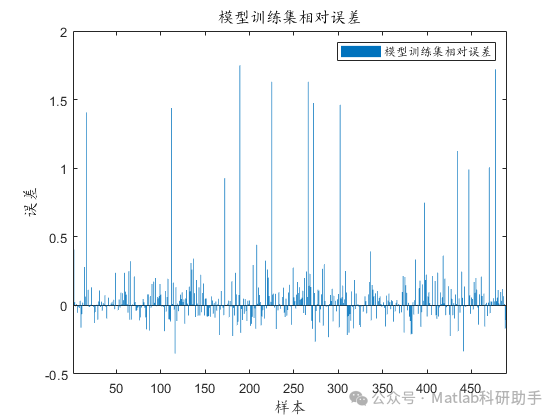
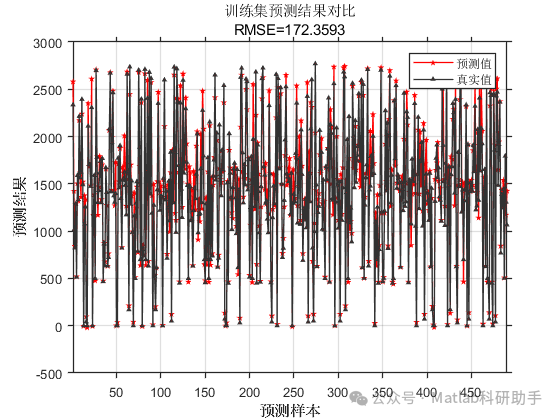
⛳️ 运行结果
正在上传…重新上传取消
🔗 参考文献
🎈 部分理论引用网络文献,若有侵权联系博主删除
👇 关注我领取海量matlab电子书和数学建模资料
擅长领域:
🌈 各类智能优化算法改进及应用
生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化、背包问题、 风电场布局、时隙分配优化、 最佳分布式发电单元分配、多阶段管道维修、 工厂-中心-需求点三级选址问题、 应急生活物质配送中心选址、 基站选址、 道路灯柱布置、 枢纽节点部署、 输电线路台风监测装置、 集装箱调度、 机组优化、 投资优化组合、云服务器组合优化、 天线线性阵列分布优化、CVRP问题、VRPPD问题、多中心VRP问题、多层网络的VRP问题、多中心多车型的VRP问题、 动态VRP问题、双层车辆路径规划(2E-VRP)、充电车辆路径规划(EVRP)、油电混合车辆路径规划、混合流水车间问题、 订单拆分调度问题、 公交车的调度排班优化问题、航班摆渡车辆调度问题、选址路径规划问题、港口调度、港口岸桥调度、停机位分配、机场航班调度、泄漏源定位
🌈 机器学习和深度学习时序、回归、分类、聚类和降维
2.1 bp时序、回归预测和分类
2.2 ENS声神经网络时序、回归预测和分类
2.3 SVM/CNN-SVM/LSSVM/RVM支持向量机系列时序、回归预测和分类
2.4 CNN|TCN|GCN卷积神经网络系列时序、回归预测和分类
2.5 ELM/KELM/RELM/DELM极限学习机系列时序、回归预测和分类
2.6 GRU/Bi-GRU/CNN-GRU/CNN-BiGRU门控神经网络时序、回归预测和分类
2.7 ELMAN递归神经网络时序、回归\预测和分类
2.8 LSTM/BiLSTM/CNN-LSTM/CNN-BiLSTM/长短记忆神经网络系列时序、回归预测和分类
2.9 RBF径向基神经网络时序、回归预测和分类




















 2072
2072

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








