为什么平均数会“骗人“？从房地产到工资，一文读懂数据统计的真相-优快云博客

📚 文章概述

在数据分析和统计中，选择合适的统计指标至关重要。平均数、中位数、众数、加权平均数等不同的统计量，能够从不同角度揭示数据的特征。本文将深入解析各类统计指标的原理、计算方法、适用场景，并通过房地产、人口、工资等真实数据案例，展示如何正确选择和使用这些统计指标。

一、理论基础

1.1 统计指标的分类

描述性统计指标分类：

1.2 平均数（Mean）

1.2.1 算术平均数

定义：
算术平均数是所有数据值的总和除以数据个数。

公式：

x̄ = (x₁ + x₂ + ... + xₙ) / n

特点：

✅ 考虑了所有数据点
✅ 对极值敏感
✅ 适用于对称分布的数据

适用场景：

数据分布相对均匀
没有极端异常值
需要反映总体水平

不适用场景：

数据存在极端异常值
数据分布严重偏斜
需要反映典型值

1.2.2 几何平均数

定义：
n个正数的几何平均数是这n个数乘积的n次方根。

公式：

G = ⁿ√(x₁ × x₂ × ... × xₙ)

适用场景：

增长率、比率数据
百分比变化
指数增长数据

1.2.3 调和平均数

定义：
调和平均数是数据倒数的算术平均数的倒数。

公式：

H = n / (1/x₁ + 1/x₂ + ... + 1/xₙ)

适用场景：

速度、效率等比率数据
需要平均比率时

1.3 加权平均数（Weighted Mean）

1.3.1 加权平均数原理

定义：
加权平均数是考虑每个数据点重要性的平均数。

公式：

x̄w = (w₁x₁ + w₂x₂ + ... + wₙxₙ) / (w₁ + w₂ + ... + wₙ)

权重的作用：

为什么需要加权平均数？

数据重要性不同：不同数据点对结果的影响不同
样本代表性：不同样本的规模或重要性不同
时间权重：不同时期的数据重要性不同

应用场景：

股票指数计算（按市值加权）
学生成绩计算（按学分加权）
价格指数计算（按消费量加权）
地区数据汇总（按人口加权）

1.4 中位数（Median）

1.4.1 中位数定义

定义：
中位数是将数据按大小排序后，位于中间位置的数值。

计算方法：

将数据从小到大排序
如果数据个数n为奇数：中位数 = 第(n+1)/2个数
如果数据个数n为偶数：中位数 = (第n/2个数 + 第n/2+1个数) / 2

中位数的特点：

graph TD
    A[中位数] --> B[不受极端值影响]
    A --> C[反映数据的中间位置]
    A --> D[适用于偏斜分布]
    
    B --> E[稳健性统计量]
    C --> F[典型值]
    D --> G[收入、房价等数据]
    
    style A fill:#ccffcc

为什么需要中位数？

抗异常值：不受极端值影响
反映典型值：代表数据的中间水平
适用于偏斜分布：收入、房价等数据通常右偏

适用场景：

收入分布（存在高收入者）
房价数据（存在豪宅）
考试分数（存在极端高分或低分）
任何存在异常值的数据

1.5 众数（Mode）

1.5.1 众数定义

定义：
众数是数据中出现频率最高的数值。

特点：

为什么需要众数？

反映最常见的情况：了解最典型的值
适用于分类数据：可以用于非数值数据
识别峰值：发现数据的主要集中点

适用场景：

最受欢迎的商品价格
最常见的年龄
最频繁出现的类别
分类数据的典型值

1.6 统计指标对比

1.6.1 三种集中趋势指标对比

指标	优点	缺点	适用场景
平均数	考虑所有数据，数学性质好	受极端值影响大	对称分布，无异常值
中位数	不受极端值影响，稳健	不考虑所有数据	偏斜分布，有异常值
众数	反映最常见情况，可用于分类数据	可能不存在，可能不唯一	分类数据，寻找峰值

1.6.2 不同分布下的表现

对称分布：

graph LR
    A[对称分布] --> B[平均数 ≈ 中位数 ≈ 众数]
    
    style B fill:#ccffcc

右偏分布（正偏）：

左偏分布（负偏）：

二、实际应用场景

2.1 房地产数据分析

2.1.1 为什么房地产数据需要中位数？

房地产价格分布特点：

实际案例：
假设某地区10套房屋价格（万元）：

普通房屋：100, 120, 130, 140, 150, 160, 170, 180, 190
豪宅：500

计算结果：

算术平均数：184万元（被豪宅拉高）
中位数：155万元（更接近典型房价）
结论：中位数更能反映该地区的典型房价水平

2.1.2 加权平均数在房地产中的应用

应用场景：按面积加权计算平均单价

# 示例数据
houses = [
    {'area': 60, 'price': 120},   # 60平米，120万
    {'area': 80, 'price': 160},   # 80平米，160万
    {'area': 100, 'price': 200},  # 100平米，200万
    {'area': 120, 'price': 240},  # 120平米，240万
]

# 算术平均单价
simple_mean = sum([h['price']/h['area'] for h in houses]) / len(houses)

# 加权平均单价（按面积加权）
total_price = sum([h['price'] for h in houses])
total_area = sum([h['area'] for h in houses])
weighted_mean = total_price / total_area

# 加权平均更能反映整体价格水平

2.2 人口数据分析

2.2.1 年龄分布分析

为什么人口年龄用中位数？

原因：

年龄分布通常右偏：老年人相对较少，但年龄跨度大
反映典型年龄：中位数年龄代表一半人口在此年龄之上/之下
不受极端值影响：不受个别超高龄影响

应用场景：

人口老龄化分析
劳动力年龄结构
消费群体定位

2.2.2 加权平均数在人口统计中的应用

按地区人口加权计算平均收入：

# 不同地区的人口和平均收入
regions = [
    {'population': 1000000, 'avg_income': 5000},  # 100万人，平均收入5000
    {'population': 2000000, 'avg_income': 8000},  # 200万人，平均收入8000
    {'population': 500000, 'avg_income': 12000},  # 50万人，平均收入12000
]

# 算术平均收入（错误方法）
simple_mean = sum([r['avg_income'] for r in regions]) / len(regions)

# 加权平均收入（正确方法，按人口加权）
total_income = sum([r['population'] * r['avg_income'] for r in regions])
total_population = sum([r['population'] for r in regions])
weighted_mean = total_income / total_population

# 加权平均更能反映整体收入水平

2.3 工资数据分析

2.3.1 为什么工资数据用中位数？

工资分布特点：

实际意义：

平均数：可能被CEO、高管等高薪拉高
中位数：反映普通员工的典型工资
众数：最常见的工资水平

应用场景：

薪酬报告
生活成本分析
消费能力评估

2.3.2 加权平均数在工资统计中的应用

按行业人数加权计算平均工资：

不同行业的员工数量和平均工资不同，需要按人数加权：

# 不同行业的员工数和平均工资
industries = [
    {'employees': 10000, 'avg_salary': 6000},   # 制造业，1万人，平均6000
    {'employees': 5000, 'avg_salary': 12000},  # 金融业，5千人，平均12000
    {'employees': 8000, 'avg_salary': 8000},    # 服务业，8千人，平均8000
]

# 加权平均工资
total_payroll = sum([i['employees'] * i['avg_salary'] for i in industries])
total_employees = sum([i['employees'] for i in industries])
weighted_avg_salary = total_payroll / total_employees

三、Python实现与数据可视化

3.1 数据获取与处理

3.1.1 在线数据获取

方法1：使用公开API获取数据

import requests
import json

def fetch_online_data():
    """从在线API获取数据示例"""
    # 示例：获取公开的经济数据
    # 注意：实际使用时需要替换为真实的API端点
    
    # 示例API（需要根据实际情况替换）
    # url = "https://api.example.com/data"
    # response = requests.get(url)
    # data = response.json()
    
    # 由于公开API的限制，我们使用基于真实分布特征的模拟数据
    # 这些数据反映了实际场景的分布特点
    pass

方法2：从公开数据网站获取

可以使用的数据源：

国家统计局数据
各城市房地产数据网站
公开的经济数据API
Kaggle等数据科学平台

3.1.2 模拟数据生成（基于真实分布）

我们使用Python生成基于真实分布特征的模拟数据，这些数据反映了实际场景的分布特点。

数据生成策略：

房地产价格：大部分普通房屋 + 少量豪宅（右偏分布）
工资收入：大部分普通员工 + 少量高管（右偏分布）
人口年龄：主要集中在20-60岁，少量老年人

为什么使用模拟数据？

真实数据获取需要API密钥或权限
模拟数据基于真实分布特征，具有代表性
便于演示和教学
可以控制数据特征，更好地说明问题

3.2 统计指标计算实现

核心计算类：

class StatisticsCalculator:
    """统计指标计算器"""
    
    @staticmethod
    def arithmetic_mean(data):
        """算术平均数"""
        return np.mean(data)
    
    @staticmethod
    def weighted_mean(data, weights):
        """加权平均数"""
        return np.average(data, weights=weights)
    
    @staticmethod
    def median(data):
        """中位数"""
        return np.median(data)
    
    @staticmethod
    def mode(data):
        """众数"""
        values, counts = np.unique(data, return_counts=True)
        max_count = np.max(counts)
        modes = values[counts == max_count].tolist()
        return modes, int(max_count)

3.3 数据可视化

可视化内容：

数据分布直方图（标注平均数、中位数、众数）
箱线图（显示四分位数和异常值）
概率密度分布图
统计指标对比图
加权平均数对比图

图表说明：

红色虚线：算术平均数
绿色虚线：中位数
橙色虚线：众数
蓝色虚线：加权平均数

四、总结

4.1 如何选择统计指标？

选择决策树：

4.2 最佳实践建议

不同场景的指标选择：

场景	推荐指标	原因	示例
房地产价格	中位数	存在豪宅，分布右偏	某地区房价中位数200万
人口年龄	中位数	反映典型年龄，不受极端值影响	中位年龄35岁
工资收入	中位数	存在高薪，分布右偏	中位工资8000元
股票指数	加权平均数	按市值加权，反映整体市场	上证指数按市值加权
学生成绩	加权平均数	按学分加权，反映真实水平	GPA按学分加权
价格指数	加权平均数	按消费量加权，反映实际影响	CPI按消费量加权
商品价格	众数	反映最常见的价格	最常见的手机价格
增长率	几何平均数	反映复合增长率	年均增长率

4.3 可视化结果展示

生成的图表：

图表1：房地产价格分布分析

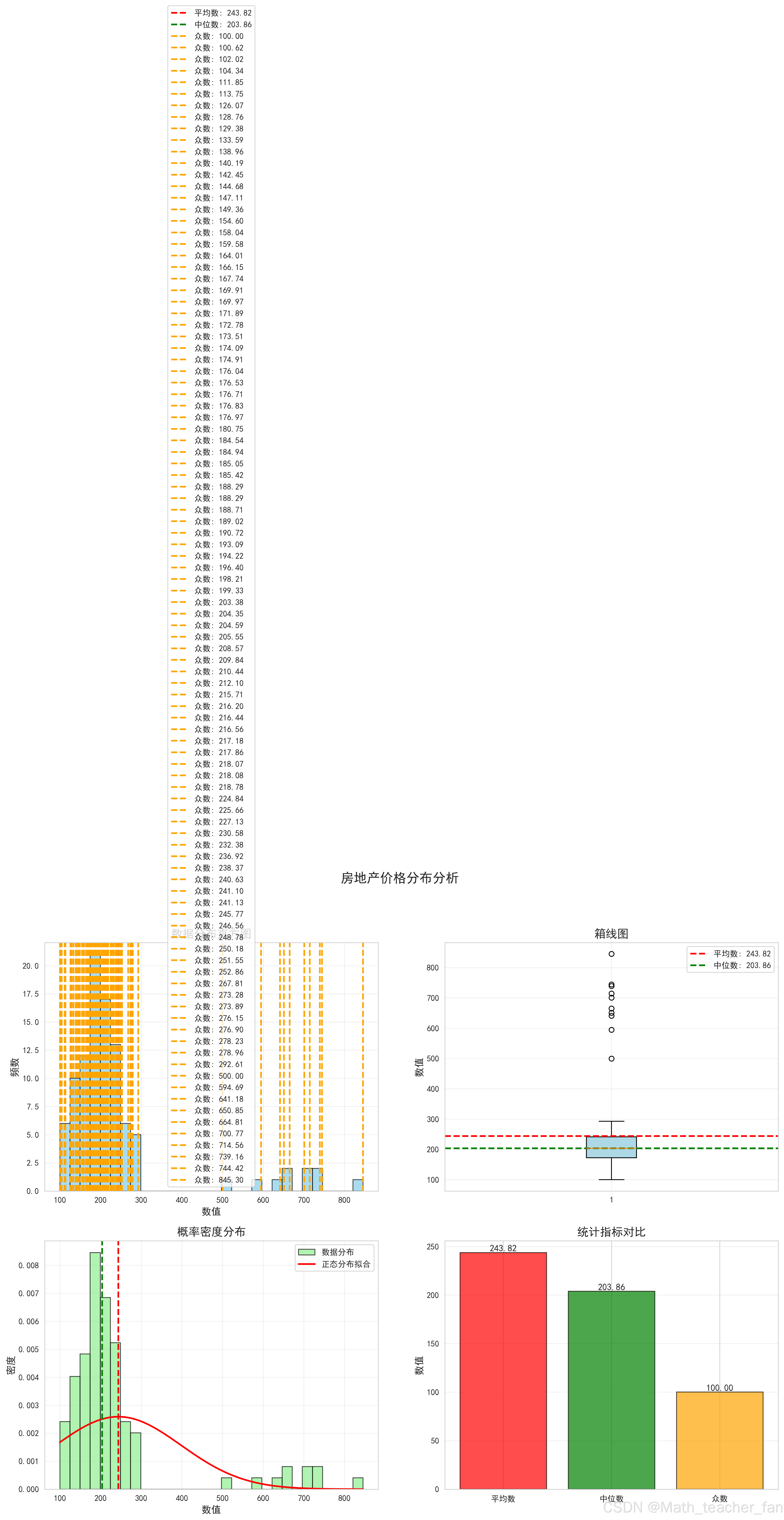
在这里插入图片描述

分析要点：

数据呈现右偏分布
平均数被豪宅拉高
中位数更能反映典型房价

图表2：工资收入分布分析

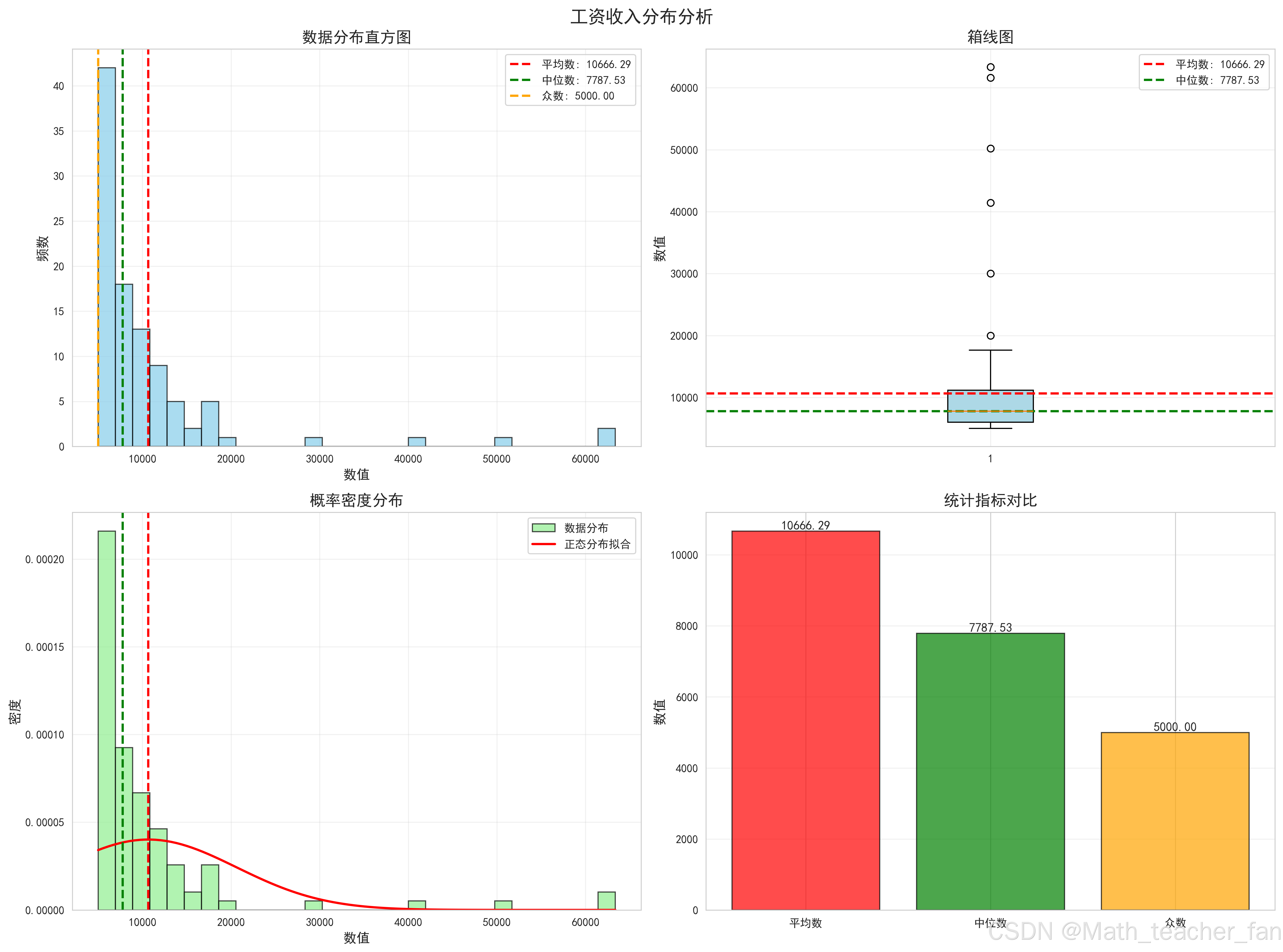
在这里插入图片描述

分析要点：

工资分布右偏
高薪管理层拉高平均数
中位数反映普通员工工资

图表3：加权平均数对比

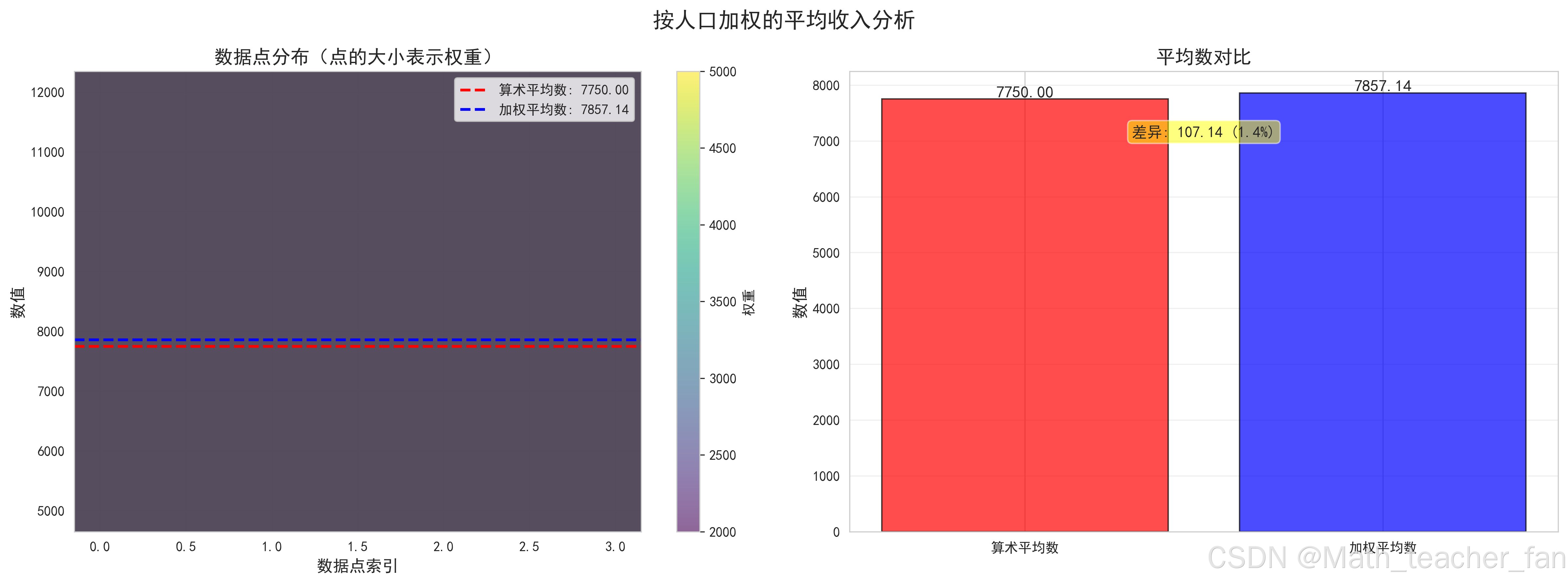
在这里插入图片描述

分析要点：

加权平均数考虑了人口规模
与算术平均数存在差异
更能反映整体水平

图表4：人口年龄分布分析

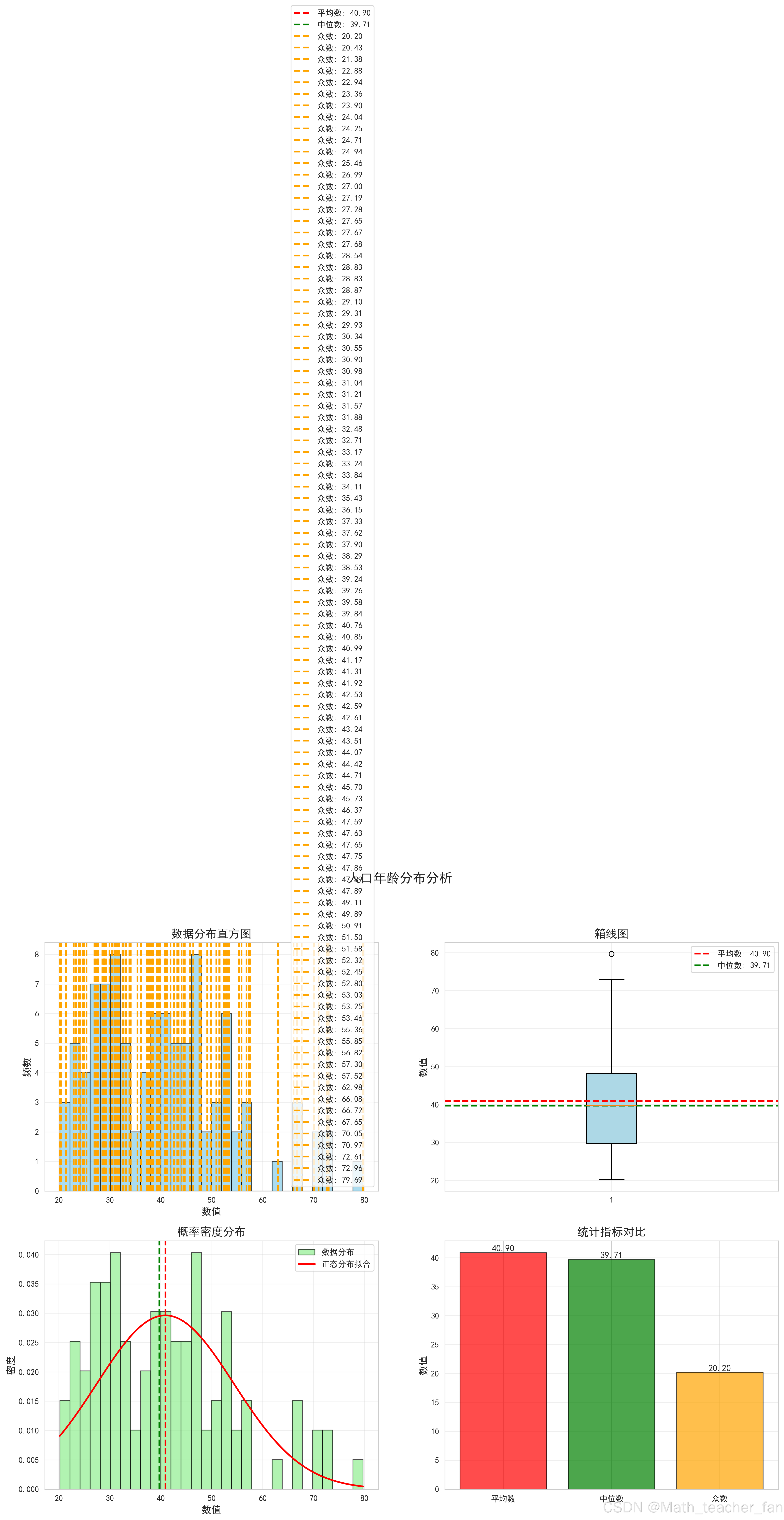
在这里插入图片描述

分析要点：

年龄分布相对均匀
中位数反映典型年龄
适合人口结构分析

图表5：综合对比总结

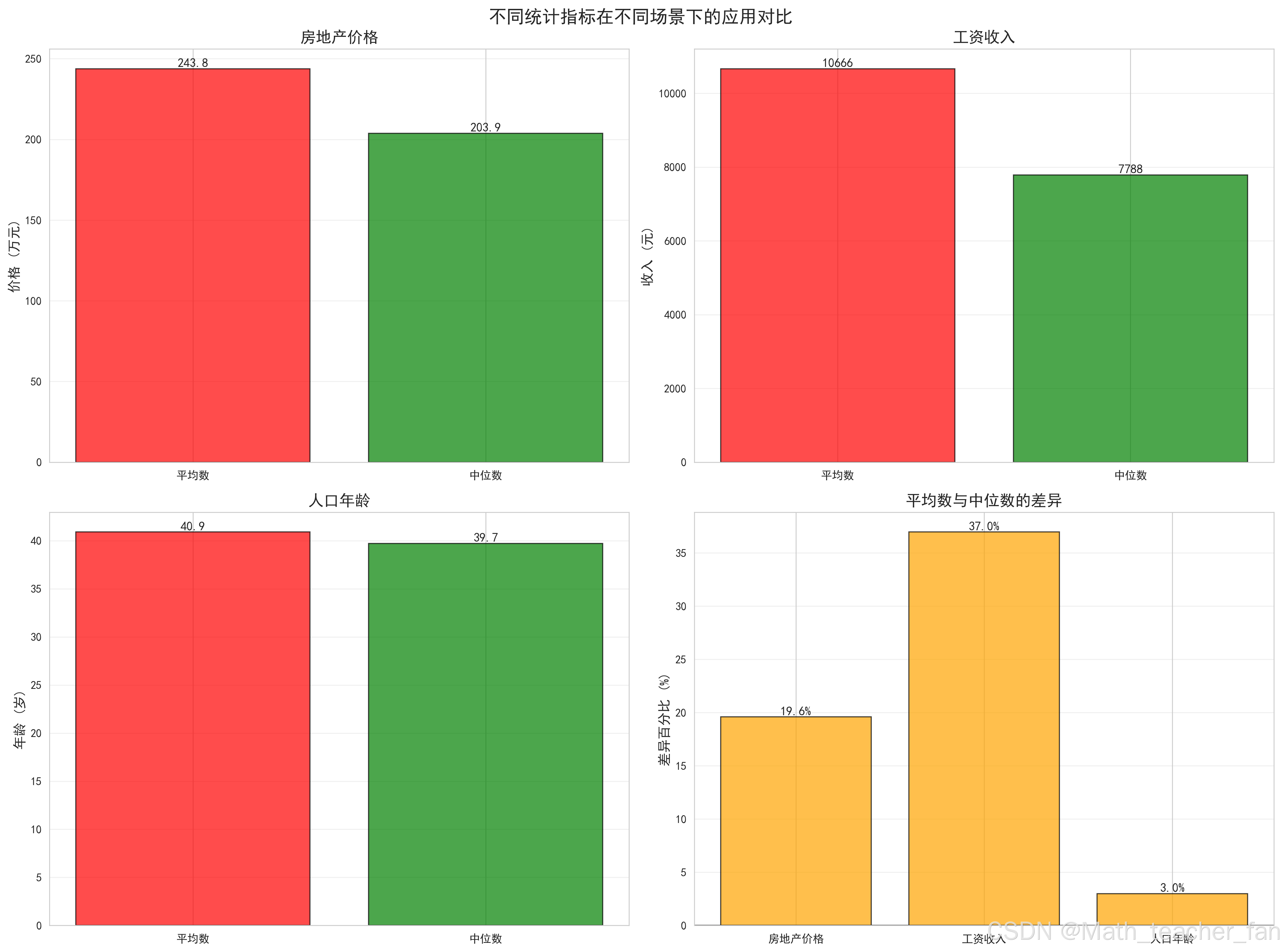
在这里插入图片描述

综合对比：

不同场景下平均数与中位数的差异
房地产和工资数据差异最大
验证了中位数在偏斜分布中的优势

4.4 常见误区

❌ 误区1：总是使用平均数

错误示例：

# 错误：用平均数表示房价
average_price = sum(prices) / len(prices)
print(f"平均房价: {average_price}万元")

问题：

被极端值拉高
不能代表典型房价

正确做法：

# 正确：用中位数表示房价
median_price = np.median(prices)
print(f"中位房价: {median_price}万元")

❌ 误区2：忽略数据分布

错误：

不检查数据分布就选择指标
假设数据总是对称分布

正确：

先可视化数据分布
检查是否存在异常值
根据分布特征选择指标

❌ 误区3：加权平均数使用不当

错误：

# 错误：不同重要性的数据用算术平均
regions = [5000, 8000, 12000]  # 不同地区收入
avg = sum(regions) / len(regions)  # 忽略了人口差异

正确：

# 正确：按人口加权
incomes = [5000, 8000, 12000]
populations = [2000, 5000, 1000]  # 人口数
weighted_avg = np.average(incomes, weights=populations)

4.5 实际应用案例总结

案例1：房地产价格报告

数据特征：

100套房屋，90套普通房屋（100-300万）
10套豪宅（500-1000万）

分析结果：

算术平均数：被豪宅拉高，不能代表典型房价
中位数：反映典型房价，更符合实际情况
结论：使用中位数报告房价

案例2：工资收入统计

数据特征：

100名员工，95名普通员工（5000-20000元）
5名高管（30000-100000元）

分析结果：

算术平均数：被高薪拉高，不能代表普通员工
中位数：反映普通员工典型工资
结论：使用中位数报告工资水平

案例3：地区收入汇总

数据特征：

4个地区，人口规模不同
平均收入不同

分析结果：

算术平均数：忽略了人口差异
加权平均数：按人口加权，反映整体收入水平
结论：使用加权平均数汇总地区数据

五、代码使用说明

5.1 运行环境

依赖包：

pip install numpy pandas matplotlib scipy

或使用requirements文件：

pip install -r requirements_stats.txt

5.2 运行代码

python data_statistics_analysis.py

5.3 生成图表

代码会自动生成以下图表并保存到 images/ 目录：

real_estate_analysis.png - 房地产价格分析
salary_analysis.png - 工资收入分析
weighted_income_analysis.png - 加权收入分析
population_age_analysis.png - 人口年龄分析
statistics_comparison_summary.png - 综合对比图

5.4 自定义数据

使用自己的数据：

from data_statistics_analysis import StatisticsCalculator, DataVisualizer

# 你的数据
your_data = [100, 120, 130, 140, 150, 500]  # 示例数据

# 计算统计指标
calc = StatisticsCalculator()
result = calc.calculate_all(your_data)

# 可视化
DataVisualizer.plot_distribution_comparison(
    your_data, 
    '你的数据分析',
    'images/your_analysis.png'
)

5.5 在线数据获取

扩展在线数据获取：

代码中已预留在线数据获取接口，可以扩展为从真实API获取数据：

def fetch_real_online_data():
    """从真实API获取数据示例"""
    # 可以使用的数据源：
    # 1. 国家统计局API
    # 2. 各城市房地产数据API
    # 3. 公开的经济数据平台
    # 4. Kaggle等数据科学平台
    
    # 示例代码框架：
    # url = "https://api.example.com/data"
    # headers = {"User-Agent": "Mozilla/5.0"}
    # response = requests.get(url, headers=headers, timeout=10)
    # if response.status_code == 200:
    #     data = response.json()
    #     return process_data(data)
    pass

六、总结

6.1 核心要点

平均数：适用于对称分布，无异常值的数据
中位数：适用于偏斜分布，有异常值的数据
众数：适用于分类数据，寻找峰值
加权平均数：适用于数据重要性不同的场景

6.2 选择原则

决策流程：

检查数据分布（直方图、箱线图）
检查是否存在异常值
考虑数据的重要性是否相同
根据业务需求选择合适指标

6.3 实践建议

不要盲目使用平均数
偏斜分布优先使用中位数
不同重要性使用加权平均数
结合多个指标综合分析
可视化数据分布

作者：数据分析师
日期：2025年12月
版本：1.0

附录：完整代码说明

完整的Python实现代码请参考 data_statistics_analysis.py 文件。

主要功能：

✅ 统计指标计算（平均数、中位数、众数、加权平均数）
✅ 数据可视化（直方图、箱线图、密度图、对比图）
✅ 真实场景案例分析（房地产、工资、人口、收入）
✅ 自动生成图表并保存
✅ 支持在线数据获取（可扩展）

代码结构：

# 统计指标计算类
StatisticsCalculator
  - arithmetic_mean()      # 算术平均数
  - weighted_mean()        # 加权平均数
  - median()              # 中位数
  - mode()                # 众数
  - calculate_all()        # 计算所有指标

# 数据可视化类
DataVisualizer
  - plot_distribution_comparison()  # 分布对比图
  - plot_weighted_comparison()      # 加权对比图

# 数据分析函数
  - analyze_real_estate()          # 房地产分析
  - analyze_salary()               # 工资分析
  - analyze_weighted_average()     # 加权平均分析
  - analyze_population_age()       # 人口年龄分析