首先我先讲解一下现实中的汉诺塔
1、有三根相邻的柱子,标号为A,B,C。
2、A柱子上从下到上按金字塔状叠放着n个不同大小的圆盘。
3、把所有盘子一个一个移动到柱子C上,并且每次移动同一根柱子上都不能出现大盘子在小盘子上方。
要写出汉诺塔的解法,我们得先了解真正的汉诺塔的解法,这里我用3层的汉诺塔做一个演示
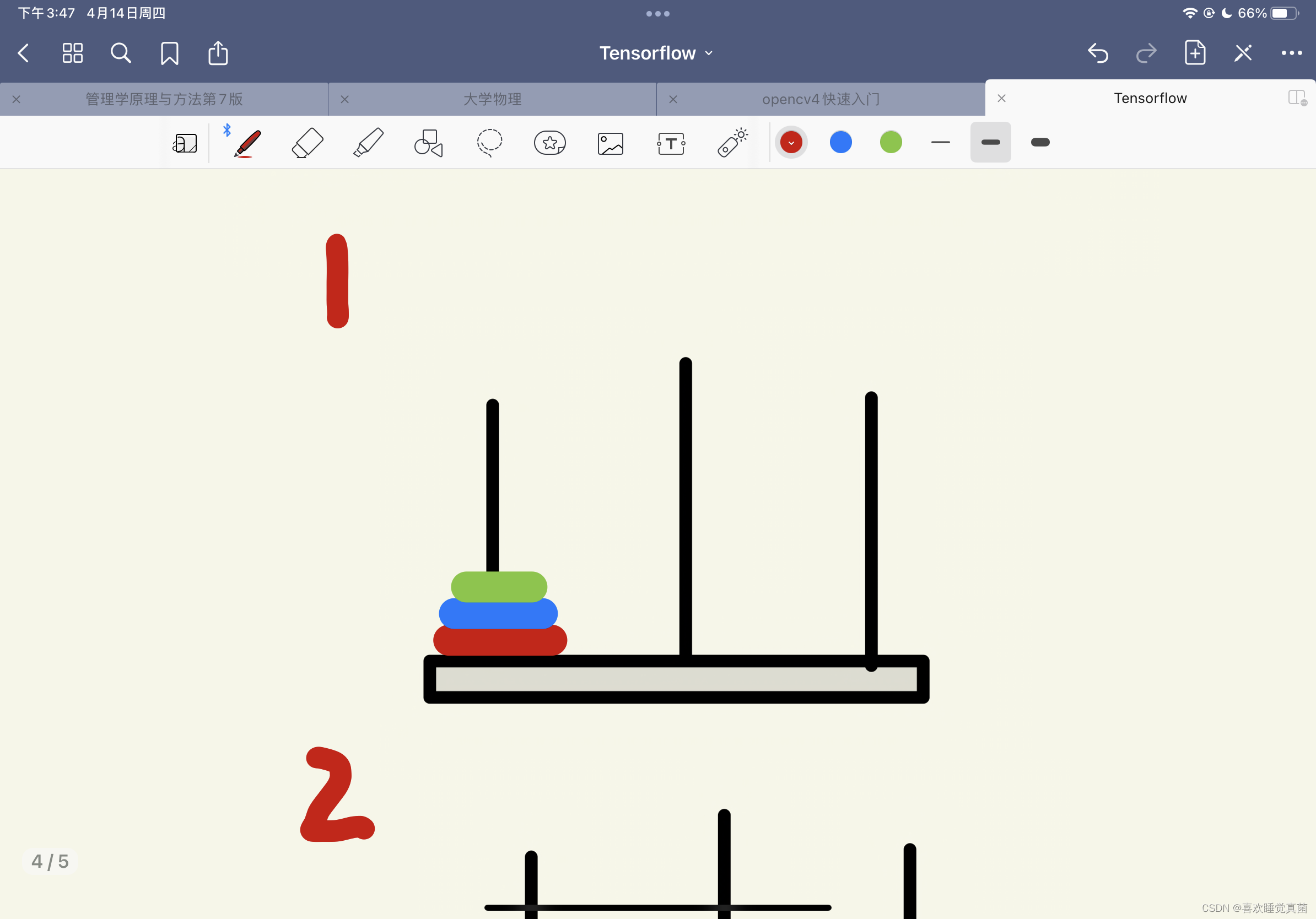
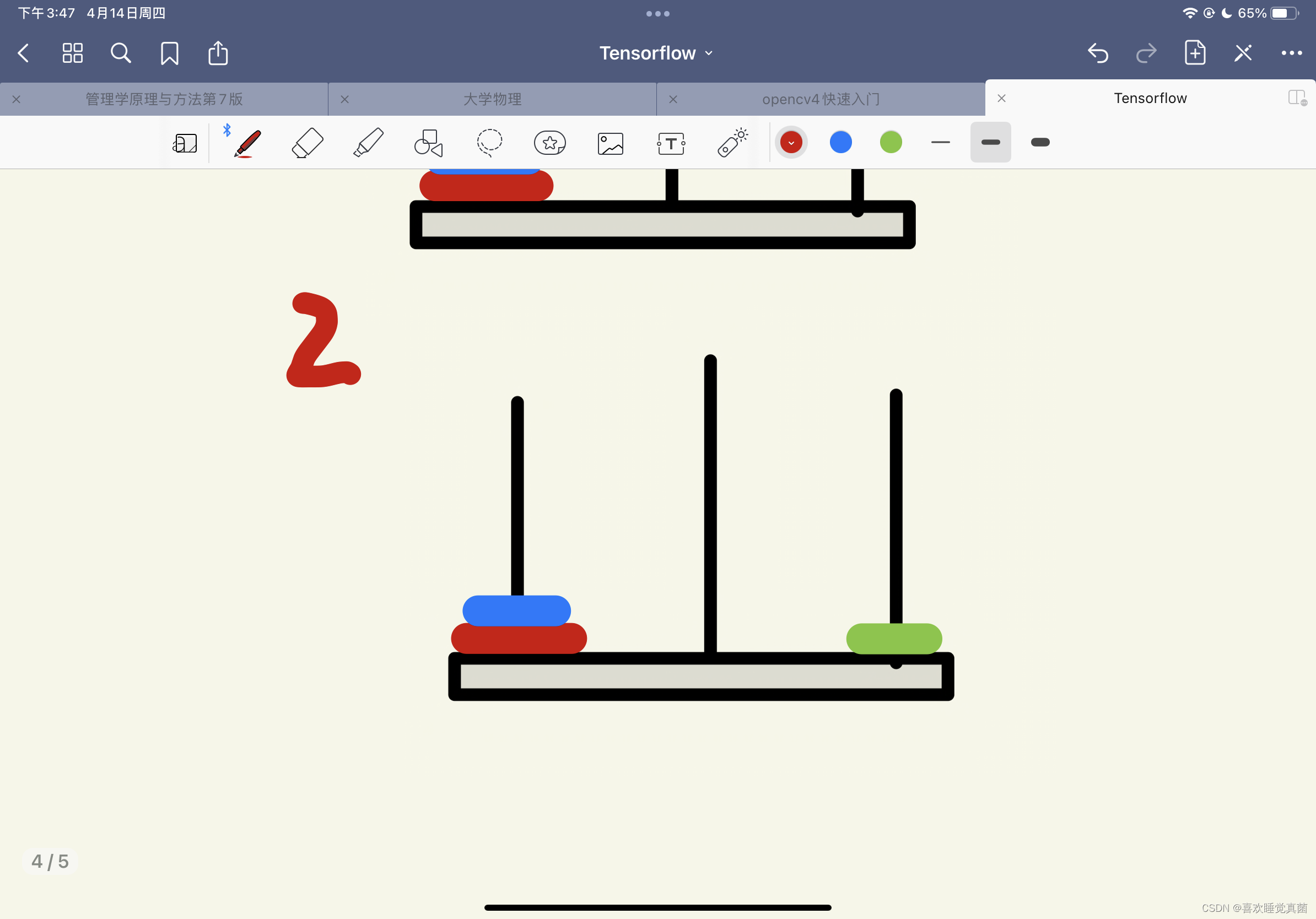
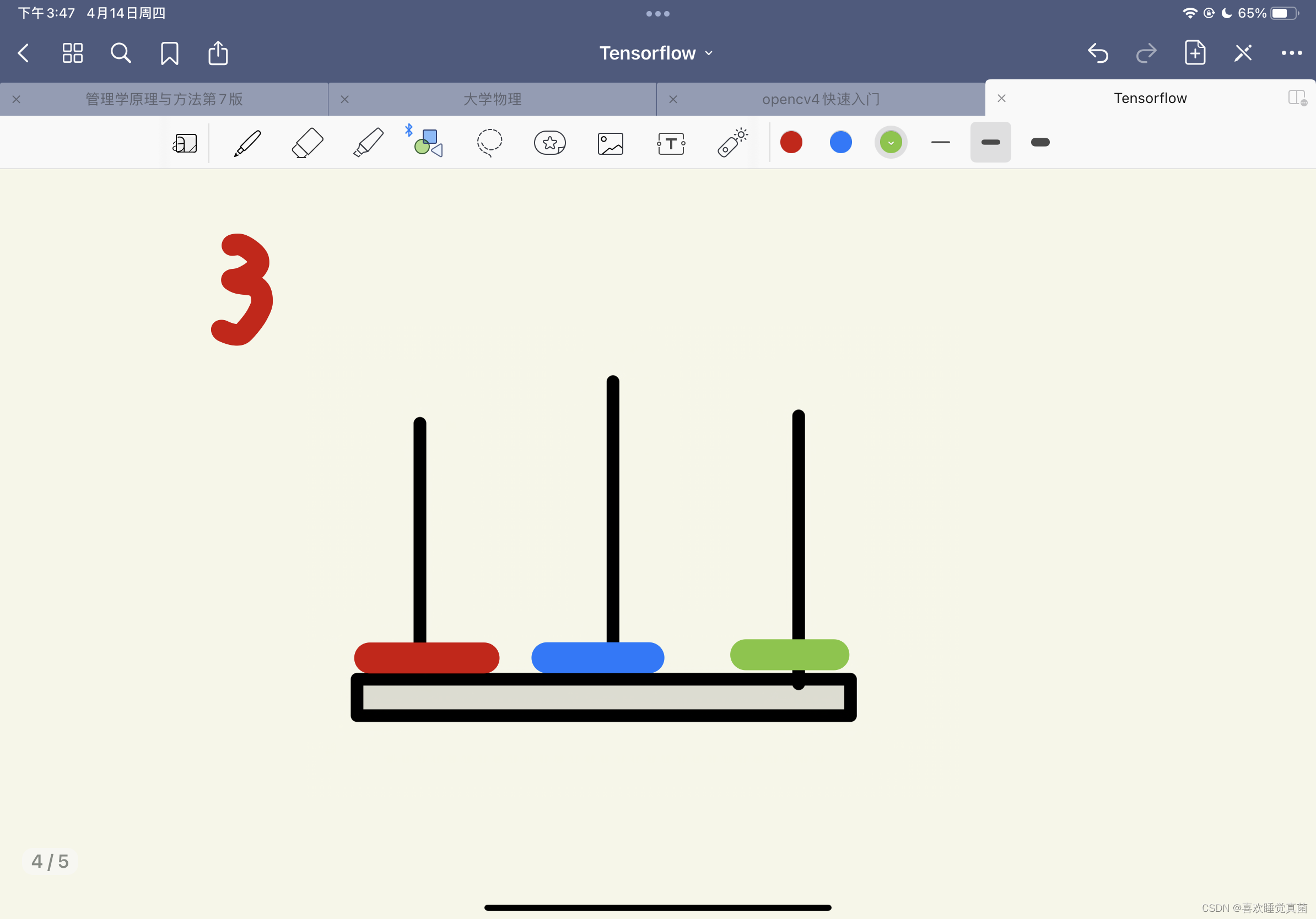
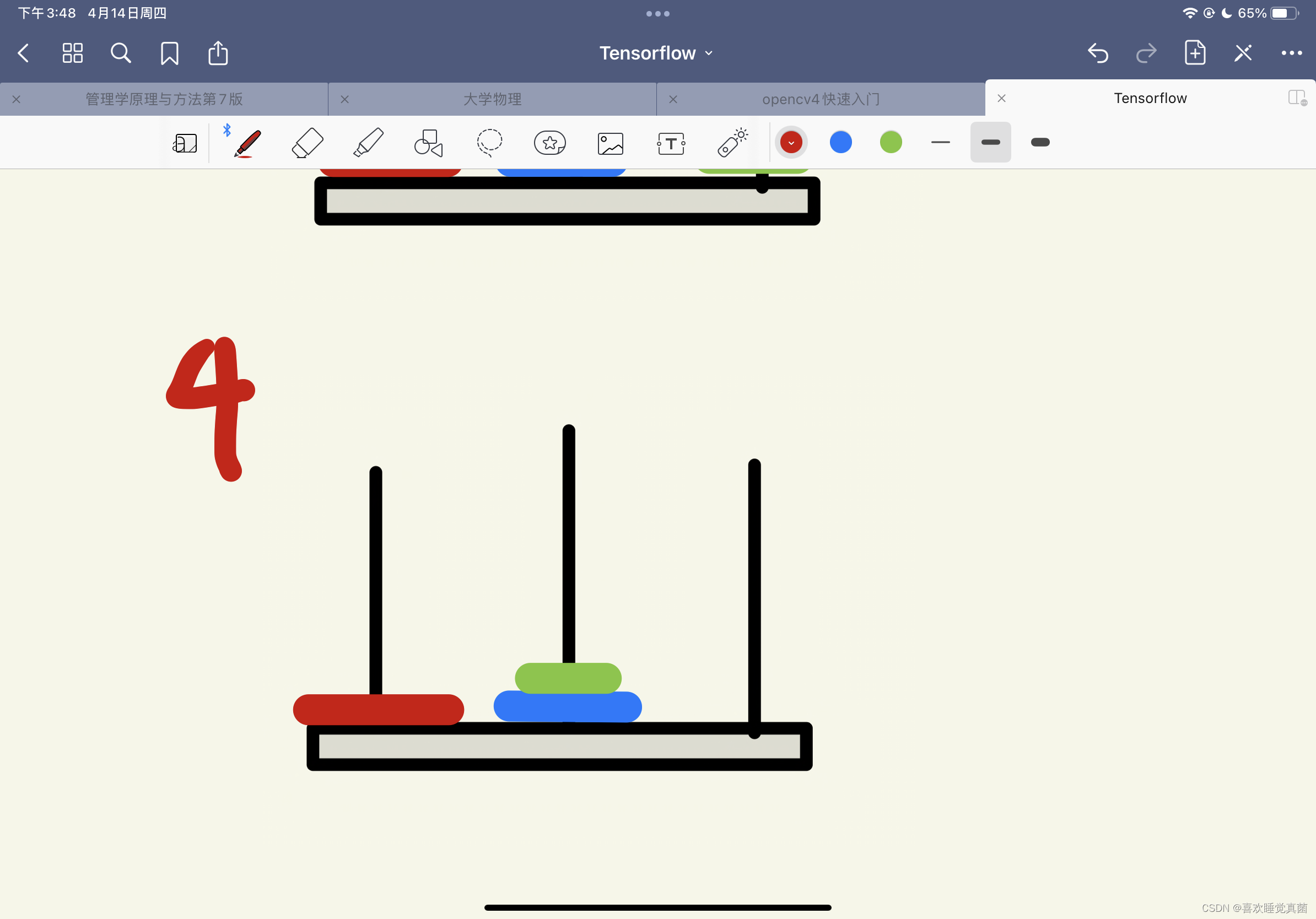
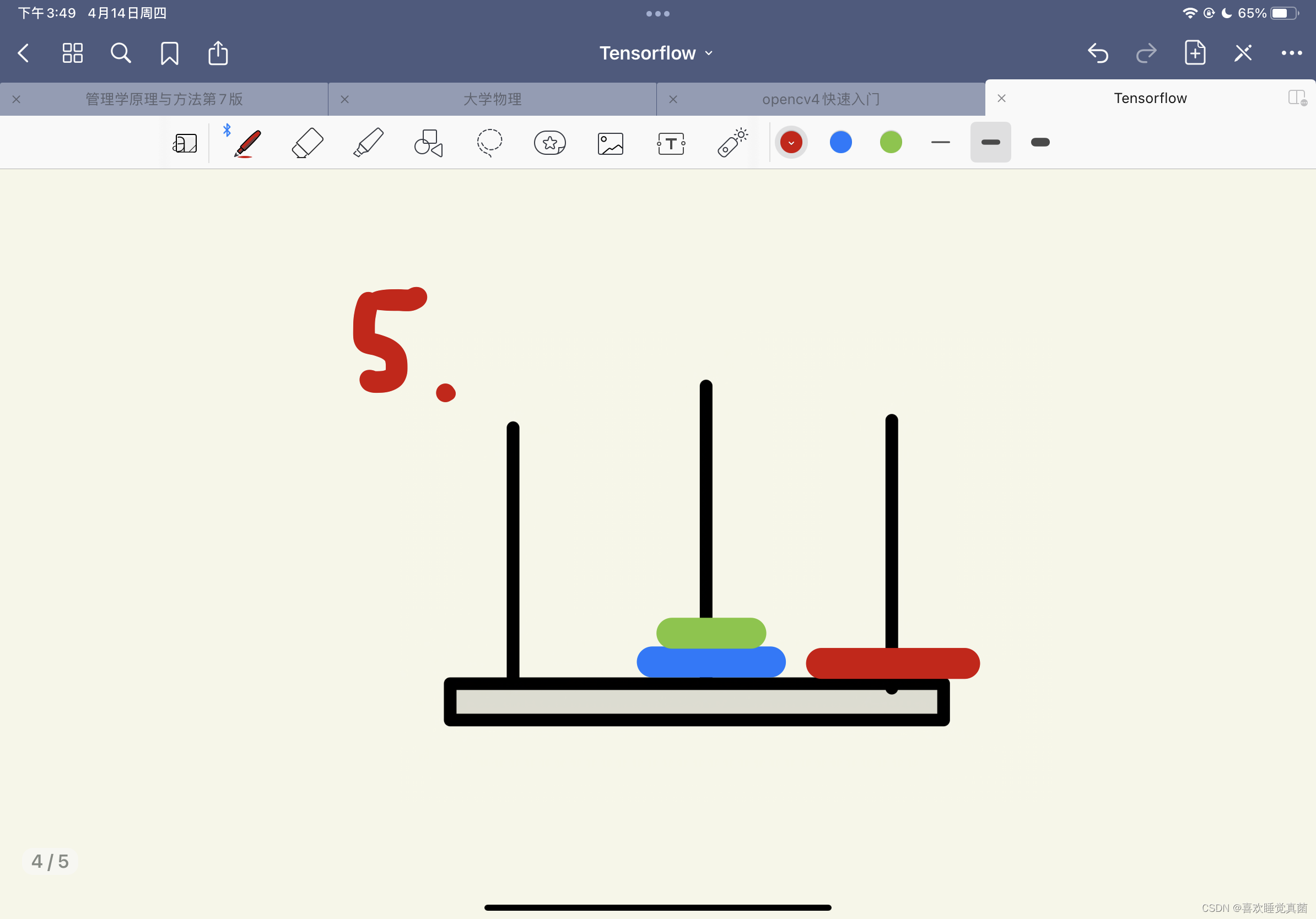
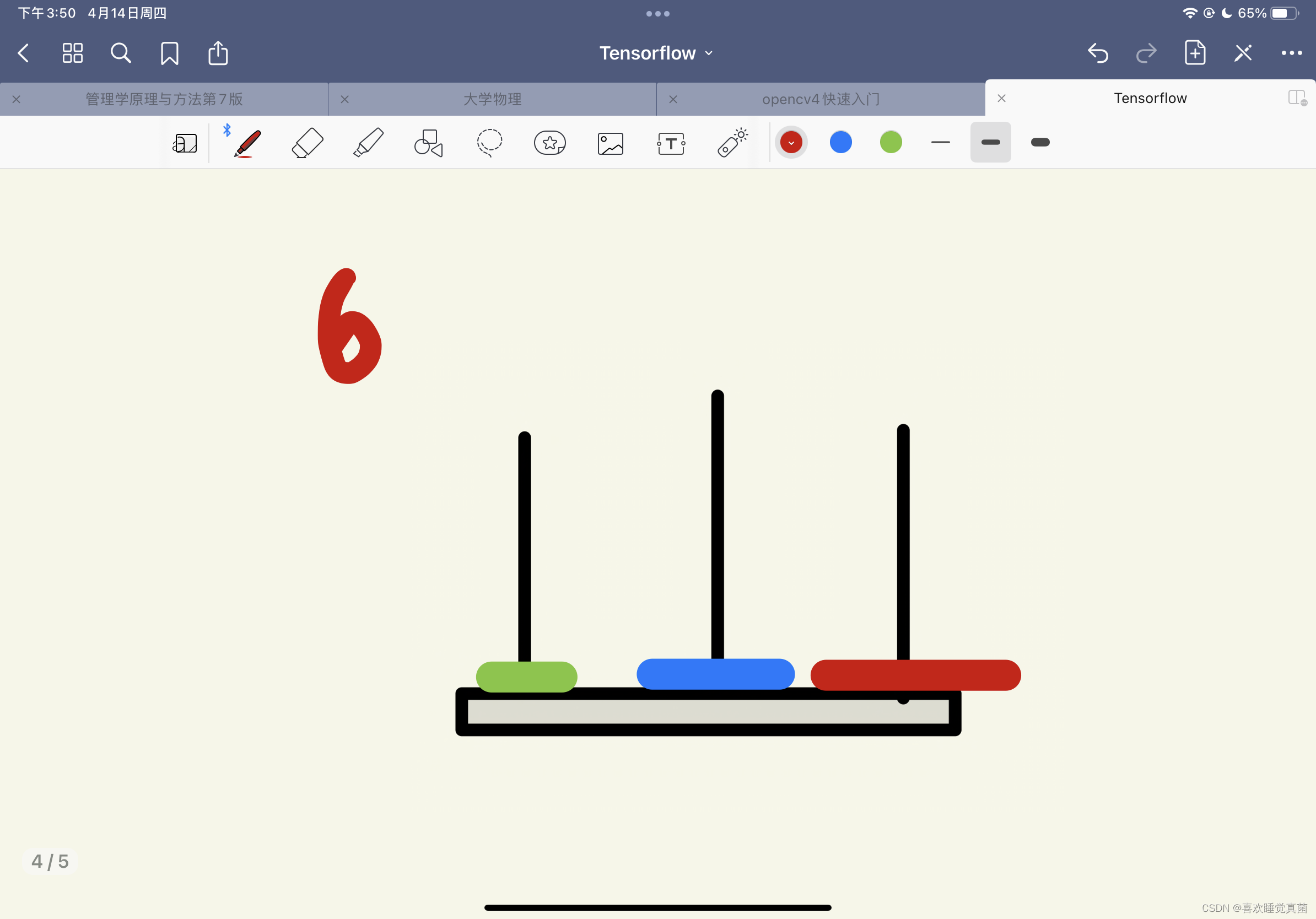
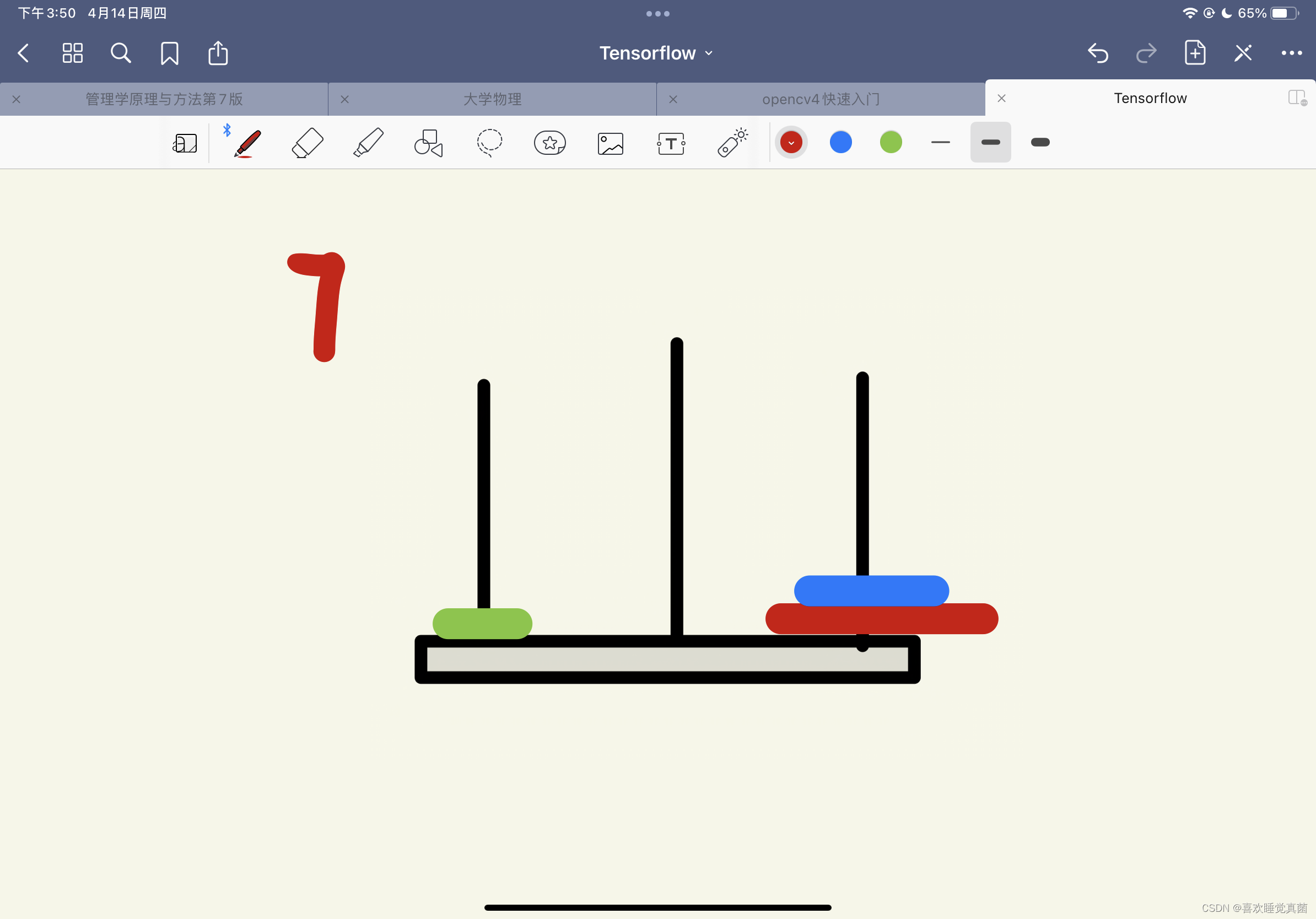
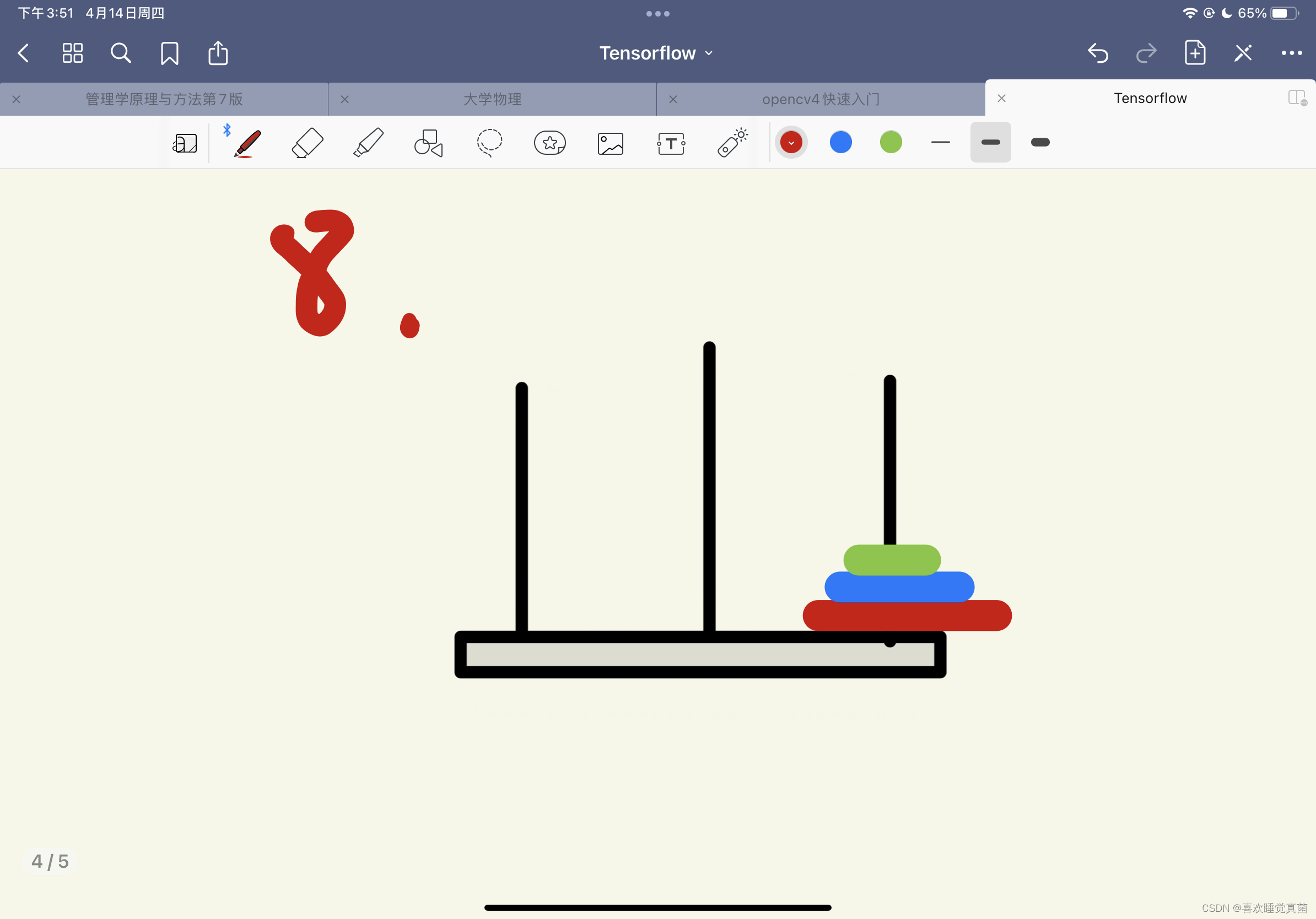
这里有关键的三步————第四步,第五步和第八步,根据这三步,我们可以将汉诺塔简化成三个步骤:
第一步,将A杆上的n - 1个圆盘经由C杆挪动到B杆上;
第二步,将最大的圆盘移动到C杆上;
第三步,将B杆上的n-1个圆盘经由A杆移动到C杆上;
接下来我们来看代码(老师示范的代码)
void move(char getfrom, char putto)
{
printf("%c--->%c\n",getfrom,putto);
}
void hanoi(int n, char source, char transition, char destination)
{
if(n==1)
move(source, destination);
else
{ hanoi(n-1, source, destination, transition);//将A柱子上的n-1个圆盘,借助柱子C,移动到柱子B上
move(source, destination );//将A柱子上的最后一个圆盘移动到柱子C上
hanoi(n-1, transition, source, destination);//将B柱子上的n-1个圆盘,借助柱子A,移动到柱子C上
}
}
main()
{ int m;
printf("Input the number of disks:");
scanf("%d",&m);
printf("The steps to moving %3d disks:\n",m);
hanoi(m,'A','B','C');
}
第一个函数move用来表示汉诺塔圆盘的移动;
第二个函数hanoi用来求解汉诺塔上面圆盘移动的过程,它有四个形参:第一个形参n代表A柱(source柱)放置圆盘的层数,source,transition,destination,分别表示A,B,C三个柱子;
if (n == 1)就是说如果只有一层,就将那层圆盘直接移动到C柱(destination)上去
如果层数大于一层,就使用之前简化的三个步骤的思路,对其进行递归,之后就能将所有圆盘移动到C柱上
下面我以3层汉诺塔为例对hanoi函数进行讲解
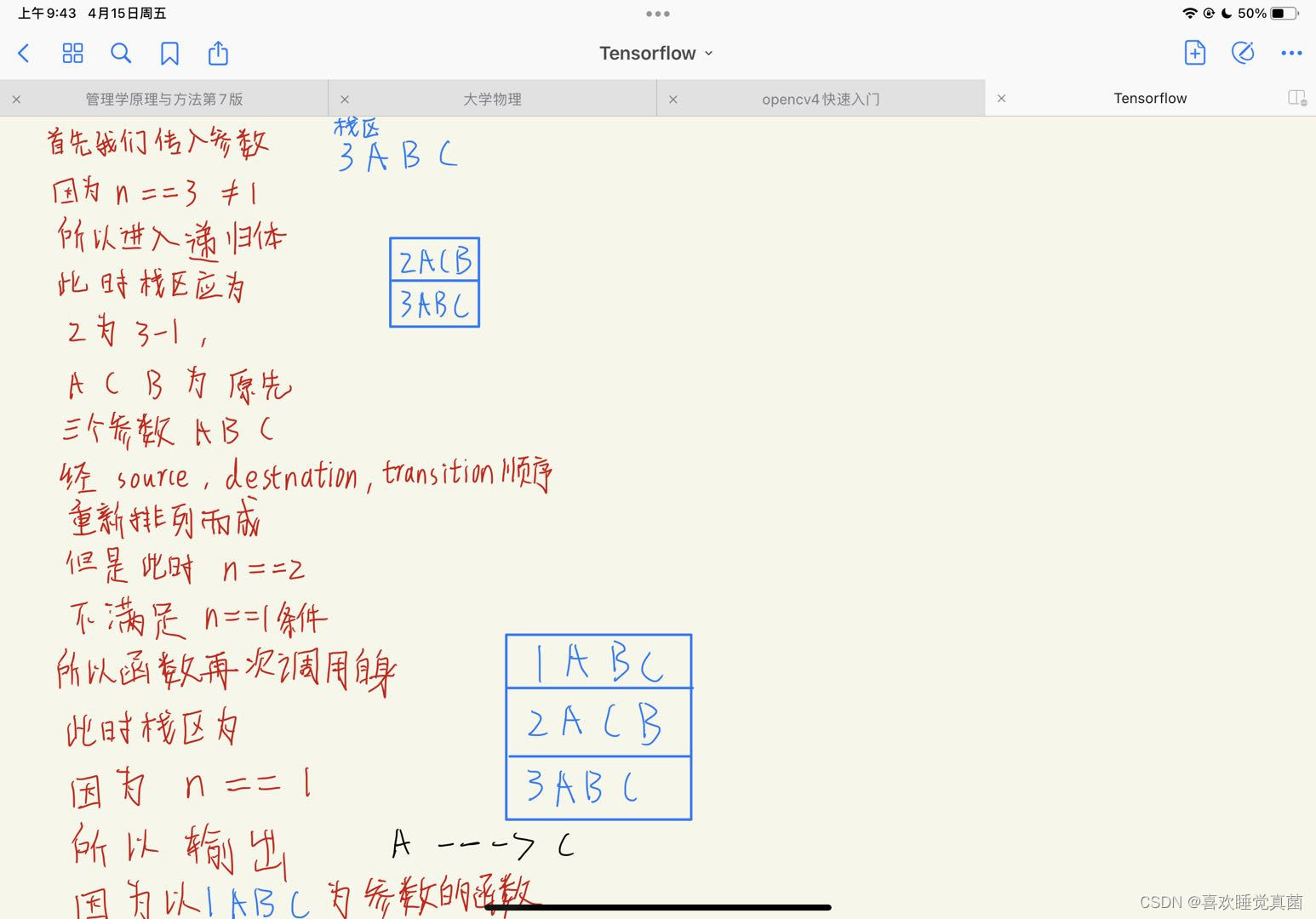






 本文详细介绍了汉诺塔问题的解决步骤,通过一个3层汉诺塔的例子展示了解决过程,并提供了相应的代码实现。核心在于理解递归思想,将问题分解为移动n-1个圆盘和移动一个圆盘两部分。代码中定义了move函数表示圆盘移动,hanoi函数作为递归主体,实现了从A柱到C柱的所有圆盘移动。
本文详细介绍了汉诺塔问题的解决步骤,通过一个3层汉诺塔的例子展示了解决过程,并提供了相应的代码实现。核心在于理解递归思想,将问题分解为移动n-1个圆盘和移动一个圆盘两部分。代码中定义了move函数表示圆盘移动,hanoi函数作为递归主体,实现了从A柱到C柱的所有圆盘移动。

















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










