如果函数变化率与函数值成正比则该函数就是一个指数函数,其外在表现为指数形式的增长或衰退。举个例子,细菌数量越多其生长率就越高;相反,放射性物质的衰变率会随着其质量的减少而变缓。但,无论是增长还是衰退其都与函数值成正比。
假设函数N 代表任意时刻t 菌群或放射性物质的数量,由于该函数的变化率与函数值成正比,则用数学语言来表示就是:
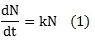
其中k 即为变化率与函数值之间的比例值,可以理解为通常意义上的斜率,其应为常数,不同类型的问题,其值不同。对于指数增长问题,k 应为正直(因为对于时刻t,函数值递增);衰退问题则应为负值(对于时刻t,函数值递减)。式(1)是一个典型的微分方程式,且其可推导出一般式:

经过上述推导,我们得到了指数问题的一般表达式,但要想用其解决实际问题还必须知道常数C 等于几。无论是菌群还是放射性物质,此类指数问题其在t=0 时刻时都会有一个初始函数值N(0),因此:
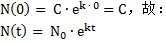
这样,我们就可以根据k及初始时刻的N值计算任意时刻t 的函数值了。
首先看这样一个实际问题:
假设一个有100万数量的菌落,30天后其菌落数量达到750万,请问何时该菌落数量能到10亿?
从已知条件我们首先计算出k 值:
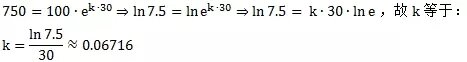
接下来就是计算何时到达10亿规模:

差不多102天就达到10亿规模 ,数量增长很客观啊。
再来看一个衰变问题:
假设某个城市受到了放射性物质钴的严重污染,经测量,当前强度为安全上限的100倍,已知钴的半衰期为5.37年,请问何时才能回到这个城市居住?
依然是根据已知条件计算k 值,半衰期为5.37年意味着要经过5.37年钴的含量才减少一半,因此:
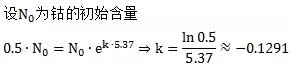
要想能够回到城市居住,钴的含量应该减少到现在的百分之一,因此:
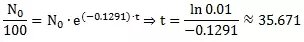
从安全角度考虑,我们最好等36年后再搬回去住。
假设函数N 代表任意时刻t 菌群或放射性物质的数量,由于该函数的变化率与函数值成正比,则用数学语言来表示就是:
其中k 即为变化率与函数值之间的比例值,可以理解为通常意义上的斜率,其应为常数,不同类型的问题,其值不同。对于指数增长问题,k 应为正直(因为对于时刻t,函数值递增);衰退问题则应为负值(对于时刻t,函数值递减)。式(1)是一个典型的微分方程式,且其可推导出一般式:

经过上述推导,我们得到了指数问题的一般表达式,但要想用其解决实际问题还必须知道常数C 等于几。无论是菌群还是放射性物质,此类指数问题其在t=0 时刻时都会有一个初始函数值N(0),因此:
这样,我们就可以根据k及初始时刻的N值计算任意时刻t 的函数值了。
首先看这样一个实际问题:
假设一个有100万数量的菌落,30天后其菌落数量达到750万,请问何时该菌落数量能到10亿?
从已知条件我们首先计算出k 值:
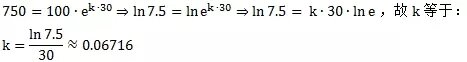
接下来就是计算何时到达10亿规模:

差不多102天就达到10亿规模 ,数量增长很客观啊。
再来看一个衰变问题:
假设某个城市受到了放射性物质钴的严重污染,经测量,当前强度为安全上限的100倍,已知钴的半衰期为5.37年,请问何时才能回到这个城市居住?
依然是根据已知条件计算k 值,半衰期为5.37年意味着要经过5.37年钴的含量才减少一半,因此:
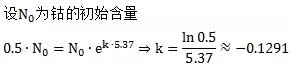
要想能够回到城市居住,钴的含量应该减少到现在的百分之一,因此:
从安全角度考虑,我们最好等36年后再搬回去住。





 本文探讨了指数增长和衰退的数学原理,解释了当函数变化率与其值成正比时如何形成指数函数。通过微分方程解析,得出了一般解,并提供了求解实际问题的方法。例如,通过计算细菌增长的k值,预测菌群达到特定规模的时间,以及放射性物质衰变的问题,计算安全返回被污染城市的时间。
本文探讨了指数增长和衰退的数学原理,解释了当函数变化率与其值成正比时如何形成指数函数。通过微分方程解析,得出了一般解,并提供了求解实际问题的方法。例如,通过计算细菌增长的k值,预测菌群达到特定规模的时间,以及放射性物质衰变的问题,计算安全返回被污染城市的时间。
















 2886
2886

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








