【三维数域】什么是空间索引，为什么需要空间索引？

最新推荐文章于 2025-10-26 15:00:19 发布

原创最新推荐文章于 2025-10-26 15:00:19 发布 · 1.1k 阅读

23 ·

CC 4.0 BY-SA版权

文章标签：

#数据库

三维数域专栏收录该内容

18 篇文章

订阅专栏

在信息技术飞速发展的时代，数据规模的指数级增长成为数据管理领域不可忽视的挑战。尤其是地理信息系统（GIS）、建筑信息建模（BIM）、虚拟现实（VR）等领域的大规模空间数据，其高维度与复杂性远超传统数据。这使得高效检索和存储成为关键问题。

传统的数据库索引结构（如B树、哈希表）无法满足空间数据的复杂查询需求，因此催生了空间索引这一关键技术。空间索引不仅通过优化数据存储结构提升查询效率，还为空间数据的分析、计算提供了强有力的支持。

一、空间索引的定义与特点

#空间索引的定义

空间索引是一种专门为管理空间数据（如点、线、面或体等几何对象）而设计的数据结构。它通过对空间数据进行划分、组织和索引，加速空间范围查询、邻近查询、最近邻搜索等操作。空间索引不仅记录数据的属性，还存储数据在空间中的位置及其几何特性。

图源：百度

#空间索引的特点

与传统索引相比，空间索引具有以下显著特点：

多维性：传统索引通常用于一维数据（如数值、文本等），而空间索引需管理多维数据，如二维平面或三维立体空间。
几何复杂性：空间索引不仅需要记录对象的位置，还需处理复杂的几何关系（如包含、相交、邻接等）。
动态性：许多空间数据应用场景（如游戏、仿真）要求索引能够实时更新，适应动态变化的空间数据。

二、为什么需要空间索引

#海量数据的管理需求

现代技术生成的空间数据规模庞大，例如城市三维建模、LIDAR扫描、卫星遥感影像等。这些数据动辄达到数十亿甚至数千亿条，如果没有高效的索引机制，逐一扫描所有数据进行查询将耗费极大的时间和计算资源。

空间索引通过构建层次结构或划分空间，大幅缩小检索范围，提升了查询效率。

#提升查询效率

空间索引的核心优势在于其能够显著加快查询速度。典型的空间查询包括：

范围查询：检索指定空间范围内的所有对象，例如查询某个城市区域内的建筑物。
邻近查询：查找某个点或对象附近的其他对象，例如在导航系统中查询最近的加油站。
最近邻搜索（k-NN查询）：查找距离最近的k个对象，例如查找某点附近最近的餐馆或医院。

通过空间索引，这些查询操作的时间复杂度可以从线性复杂度（O(n)）降至对数或更低（O(log n)）。

#满足多种空间应用场景

空间索引广泛应用于诸多领域：

GIS与遥感：空间索引用于高效检索地理实体或地理区域。
BIM与建筑规划：索引结构帮助快速定位特定的建筑部件或区域。
无人驾驶与机器人导航：实时路径规划与障碍物检测需要快速定位空间对象。

图源：百度

三、常见的空间索引方法

#R树及其变体

R树是最经典的空间索引结构之一。它利用最小边界矩形（MBR）来表示数据对象，将空间数据递归地组织成树状结构。其变体包括：

R*树：在查询操作中，MBR之间的重叠减少后，树的访问路径更加集中，从而提升查询效率。在大多数应用场景（特别是范围查询）中，性能优于标准R树。
R+树：查询时，访问的节点数量更少，特别是点查询（Point Query）和等值查询中性能更高。对于精确检索的场景（如GIS中的点定位）表现优异。

一个R树实例

#四叉树与八叉树

四叉树用于二维空间，八叉树用于三维空间，通过递归地将空间划分为四或八个子区域进行管理。它们适用于点云数据、三维模型等的快速空间划分。

四叉树与八叉树

#K-D树

K-D树是一种k维空间的索引结构，通常用于最近邻搜索。它通过按维度递归划分空间，能够高效地处理低维空间数据。

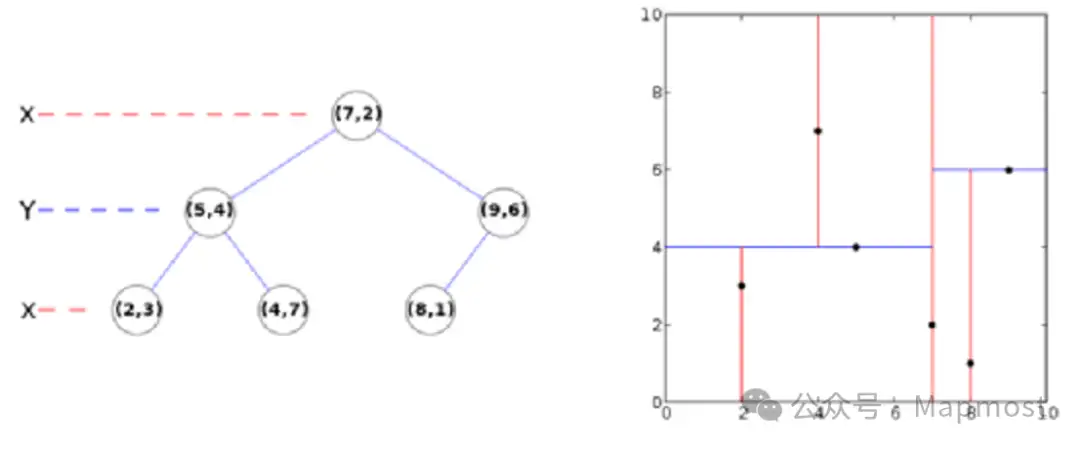
一个K-D树实例

四、空间索引的挑战与发展趋势

#挑战

高维数据管理：随着应用复杂度增加，高维空间数据（如4D、5D）索引的设计难度加大。
动态数据的实时更新：许多应用场景（如游戏、实时监控）要求索引能够实时更新，这对传统索引结构提出了更高的要求。

#发展趋势

未来空间索引的发展趋势包括：

并行化与分布式：在云计算与大数据环境下，空间索引需要支持并行与分布式计算。
机器学习与智能优化：利用机器学习优化索引结构，提高检索效率。
GPU加速：利用GPU的强大计算能力，加速空间索引的构建与查询过程。

空间索引作为大规模空间数据管理的核心技术，极大地提升了数据检索与处理效率。在未来，随着空间数据规模的持续增长与应用场景的不断丰富，空间索引将继续发挥重要作用，并在高维索引、动态更新、并行计算等方面迎来新的突破。

关注 Mapmost，持续更新 GIS、三维美术、计算机技术干货

Mapmost 是一套以三维地图和时空计算为特色的数字孪生底座平台，包含了空间数据管理工具（Studio）、应用开发工具（SDK）、应用创作工具（Alpha）。平台能力已覆盖城市时空数据的集成、多源数据资源的发布管理，以及数字孪生应用开发工具链，满足企业开发者用户快速搭建数字孪生场景的切实需求，助力实现行业领先。

点击此处前往Mapmost官网体验！