基尼系数与相关计算方法

基尼系数 (Gini coefficient) 是衡量收入分配或财富分配不平等程度的常用指标。它通常介于 0 和 1 之间，0 表示完全平等（每个人拥有相同的收入或财富），1 表示完全不平等（所有收入或财富都集中在一个人手中）。

虽然基尼系数的定义是基于洛伦茨曲线 (Lorenz curve)，但在实际计算中，有几种常用的公式，它们本质上是等价的，但适用于不同类型的数据或计算场景。

---

1. 洛伦茨曲线面积法（定义式）

这是基尼系数最直观的定义方式，基于洛伦茨曲线图。

洛伦茨曲线：将人口按收入从低到高排序，横轴表示人口的累计百分比，纵轴表示这部分人口所拥有的收入的累计百分比。如果收入完全平等，洛伦茨曲线将是一条 45 度对角线（称为绝对平等线）。实际的收入分配曲线会在这条对角线的下方。

公式：

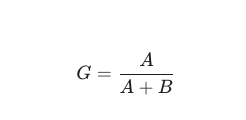
其中：

• A：绝对平等线与实际洛伦茨曲线之间的面积。

• B：实际洛伦茨曲线下方的面积。

• A + B：绝对平等线下方的总面积，在一个单位正方形图中，这个面积通常是 0.5。

因此，该公式也可以表示为：

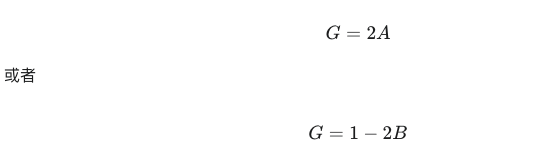
区别： 这种公式是基尼系数的概念性定义，它强调基尼系数是洛伦茨曲线与绝对平等线之间面积占总面积的比例。它在理论分析和图示解释中非常有用，但在实际数据计算时，直接测量面积 A 和 B 往往需要积分或其他更复杂的数值方法。

---

2. 离散数据排序法（基于个体数据）

当你有每个个体（或家庭）的收入数据时，可以使用这种公式。这种方法计算的是所有收入差异的平均值与总平均收入的比值。

假设有 n 个个体，他们的收入分别为 y1​,y2​,…,yn​，且已经按非降序排列 (y1​≤y2​≤⋯≤yn​)。

公式：

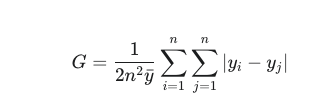
其中：

• n 是个体总数。

• yˉ​ 是平均收入（即 yˉ​=n1​∑i=1n​yi​）。

• ∣yi​−yj​∣ 表示任意两个个体收入之间的绝对差值。

更常用的排序简化公式： 对于已排序的数据 (y1​≤y2​≤⋯≤yn​)，可以简化为：

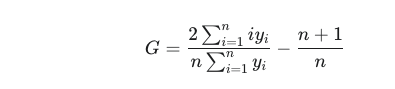
其中 i 是收入 yi​ 在排序后的排名（从 1 到 n）。

区别：

• 这种公式直接从个体数据出发，计算所有收入对之间差异的相对平均值。

• 它避免了绘制洛伦茨曲线和计算面积的步骤，更适合直接从原始数据进行编程计算。

• 公式中涉及到对数据进行排序，这在计算中是重要的一步。

• 对于小样本数据，为了得到无偏估计，有时会在分母上对 n2 进行校正，例如使用 n(n−1) 而不是 n2，但对于大样本而言，影响很小。

---

3. 梯形法（基于分组数据）

当数据以分组形式给出（例如，不同收入区间的家庭数量和其收入份额）时，可以使用梯形法来近似计算基尼系数。这实际上是洛伦茨曲线面积法的离散近似。

假设有 k 个收入组，每个组的人口比例为 pi​，收入累计比例为 Yi​ (洛伦茨曲线上的点)。

公式： 通常表示为：

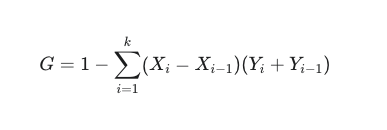
其中 Xi​ 是累计人口比例，Yi​ 是累计收入比例。通常设定 X0​=0,Y0​=0。

区别：

• 这种公式适用于分组数据，例如政府发布的收入分布报告。

• 它通过将洛伦茨曲线下的区域近似为一系列梯形或三角形的和来计算面积，从而得到基尼系数。

• 计算结果是洛伦茨曲线面积法的近似值，分组越细，近似度越高。

---

总结与区别

特征	洛伦茨曲线面积法	离散数据排序法	梯形法（分组数据）
本质	基尼系数的几何定义，基于曲线下面积	基于所有个体对收入差异的平均相对值	洛伦茨曲线面积法的离散近似
数据要求	理论概念，实际计算需转化为离散或分组数据	个体原始数据，需进行排序	分组数据（人口比例和收入比例）
计算方式	面积 A / (A + B)	收入差值的和 / (2 * n² * 平均收入) 或排序简化公式	通过计算梯形面积之和来近似洛伦茨曲线下的面积
优点	直观易懂，便于概念解释	精度高，适用于原始数据，便于编程实现	适用于统计局等发布的分组数据，操作相对简单
缺点	不便于直接计算	计算量可能较大（尤其是未排序时），需对数据排序	是近似值，精度取决于分组的细致程度