第7章习题

最新推荐文章于 2025-12-20 09:26:15 发布

原创最新推荐文章于 2025-12-20 09:26:15 发布 · 427 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#python #numpy #机器学习

7.1

import numpy as np
from scipy.interpolate import lagrange, interp1d
import pylab as plt
from scipy.integrate import quad
 
y= lambda  x:((3*x**2+x*4+6)*np.sin(x))/(x**2+x*8+6)
x=np.linspace(0,10,1000)
x0 = np.array([0, 2, 5, 10])
y0 = y(x0)
p = lagrange(x0, y0)
yx3=interp1d(x0,y0,'cubic')
y3=yx3(x)
#p = lagrange(x0,y(x0))
integral, _ = quad(y, 0, 10)
a,_=quad(yx3,0,10)
print("积分结果:", integral)
print("积分结果:", a)
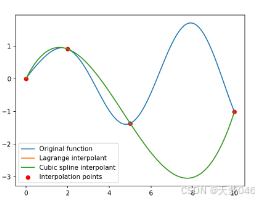
# 绘图
plt.plot(x, y(x), label='Original function')
plt.plot(x, p(x), label='Lagrange interpolant')
plt.plot(x, y3, label='Cubic spline interpolant') #插值函数
plt.scatter(x0, y0, color='red', label='Interpolation points')
plt.legend() #添加图例
 
#plt.plot(x0,y(x0))
plt.show()

结果：

7.3

import numpy as np
from scipy.interpolate import lagrange, interp1d
import pylab as plt
T =np.array([700,720,740,760,780])
V=np.array([0.0977,0.1218,0.1406,0.1551,0.1664])
x=np.linspace(750,770,1000)
x0 = np.array([750,770])
yx1 = interp1d(T,V)
y1=yx1(x)
p = lagrange(T, V)
yx3=interp1d(T,V,'cubic')
y3=yx3(x)
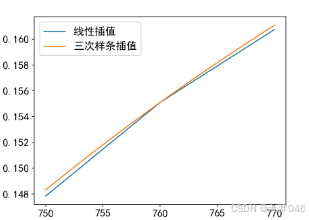
plt.rc('font',size=15,family='SimHei')
plt.rc('axes',unicode_minus=False)
plt.plot(x,y1,label='线性插值')
plt.plot(x, y3, label='三次样条插值')
plt.legend()
plt.show()

结果：

7.4

import numpy as np
from scipy.interpolate import griddata
import pylab as plt
import random
yx= lambda  x,y:(x**2-x*2)*np.exp(-x**2-y**2-x*y)
x_list = []
y_list = []
for i in range(4):
    x1 = random.uniform(-3, 3)
    y1 = random.uniform(-4, 4)
    #x_list.append([x1,y1])
    x_list.append(x1)
    y_list.append(y1)
#y0 = np.array([random.uniform(-3, 3) for _ in range(4)])
x0=np.array(x_list)
y0=np.array(y_list)
p=yx(x0,y0)
print(x0,y0)
grid_x, grid_y = np.mgrid[-3:3:100j, -3:3:100j]
grid_z = griddata((x0, y0), y0, (grid_x, grid_y), method='cubic')
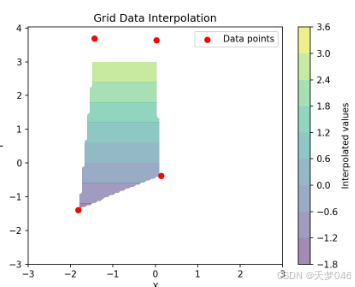
plt.scatter(x0, y0, c='red', label='Data points')
plt.contourf(grid_x, grid_y, grid_z, cmap='viridis', alpha=0.5)
plt.rc('font')
plt.colorbar(label='Interpolated values')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Grid Data Interpolation')
plt.legend()
plt.show()

结果：

7.7

import numpy as np
from scipy.optimize import curve_fit, leastsq, least_squares
import pylab as plt
from numpy.random import rand
g=lambda a,b,x:(a*10)/(b*10+(a-10*b)*np.exp(-a*np.sin(x)))
a=1.1
b=0.01
x0=np.arange(1,21)
z=g(a,b,x0)
p1,m1=curve_fit(g,x0,z,p0=rand(2))
print(p1)
def gf(p,x):
    a,b=p
    return (a*10)/(b*10+(a-10*b)*np.exp(-a*np.sin(x)))
err=lambda p,x,y:gf(p,y)-y
pa2=leastsq(err,rand(2),args=(x0,z))[0]
pa3=least_squares(err,rand(2),args=(x0,z))
print('pa2=',pa2)
print('pa3=',pa3)

结果：

[-1.50115117e+03 1.47462219e-05]
pa2= [8.66202633 0.86625069]
pa3= message: `ftol` termination condition is satisfied.
success: True
status: 2
fun: [-2.334e+00 -2.351e+01 ... -1.160e+01 -2.359e+01]
x: [ 2.857e+01 2.867e+00]
cost: 1067.9599665053647
jac: [[-1.867e+02 1.894e+03]
[-8.345e-09 8.315e-08]
...
[-1.611e-06 1.754e-05]
[-8.345e-09 8.315e-08]]
grad: [-6.662e-04 9.209e-03]
optimality: 0.009208736873006274
active_mask: [ 0.000e+00 0.000e+00]
nfev: 27
njev: 20

7.10

import numpy as np
from scipy.interpolate import lagrange, interp1d
import pylab as plt
from scipy.optimize import curve_fit
 
x1=np.array([-2,-1.7,-1.4,-1.1,-0.8,-0.5,-0.2,0.1])
y1=np.array([0.1029,0.1174,0.1316,0.1448,0.1566,0.1662,0.1733,0.1775])
x2=np.array([0.4,0.7,1,1.3,1.6,1.9,2.2,2.5])
y2=np.array([0.1785,0.1764,0.1711,0.1630,0.1526,0.1402,0.1266,0.1122])
x3=np.array([2.8,3.1,3.4,3.7,4,4.3,4.6,4.9])
y3=np.array([0.0977,0.0835,0.0702,0.0588,0.0479,0.0373,0.0291,0.0224])
x0=np.linspace(-2,4.9,100)
y = np.concatenate((y1, y2, y3))
x= np.concatenate((x1, x2, x3))
yx1 = interp1d(x,y)
y1=yx1(x0)
p = lagrange(x, y)
yx2=interp1d(x,y,'quadratic')
yx3=interp1d(x,y,'cubic')
y3=yx3(x0)
y2=yx2(x0)
plt.rc('font',size=10,family='SimHei')
plt.rc('axes',unicode_minus=False)
plt.subplot(221)
plt.plot(x0,y1,label='线性插值')
plt.subplot(222)
plt.plot(x0, y3, label='三次样条插值')
plt.plot(223)
plt.plot(x0,y2,label='二次样条插值')
plt.legend()
plt.show()
m=len(x)
R=[]
S=[]
for n in range(1,5):
    p=np.polyfit(x,y,n)
    rmse=np.sqrt(sum((np.polyval(p,x)-y)**2)/(m-n-1))
    R.append(rmse)
    S.append(p)
ind=np.argmin(R)
print('拟合的多项式次数：',ind+1)
print(np.round(S[ind],4))
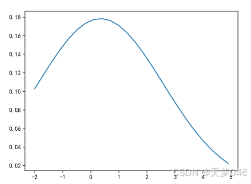
#正态分布
yx=lambda x,m,s:1/(np.sqrt(2*np.pi)*s)*np.exp(-(x-m)**2/(2*s**2))
cs=curve_fit(yx,x,y)[0]
print('拟合系数为：',np.round(cs,4))
yh=yx(x,*cs)
plt.figure()
plt.plot(x,yh)
plt.show()

结果：