二叉树生成

此次编程目的是将A(B(D(F,G),J(,L(K))),C(E(H,I)))基于这种二叉树表达形式，根据所给生成二叉树
首先是每个节点的存储类型：

typedef struct B_TREE {
	int data;
	struct B_TREE *left;
	struct B_TREE *right;
}B_TREE;

每个节点由该点数据和其左右孩子

意识到这种操作实际和表达式获取数据是类似的，在遇字符后改为指定状态进行操作，此时可以用上状态变迁图

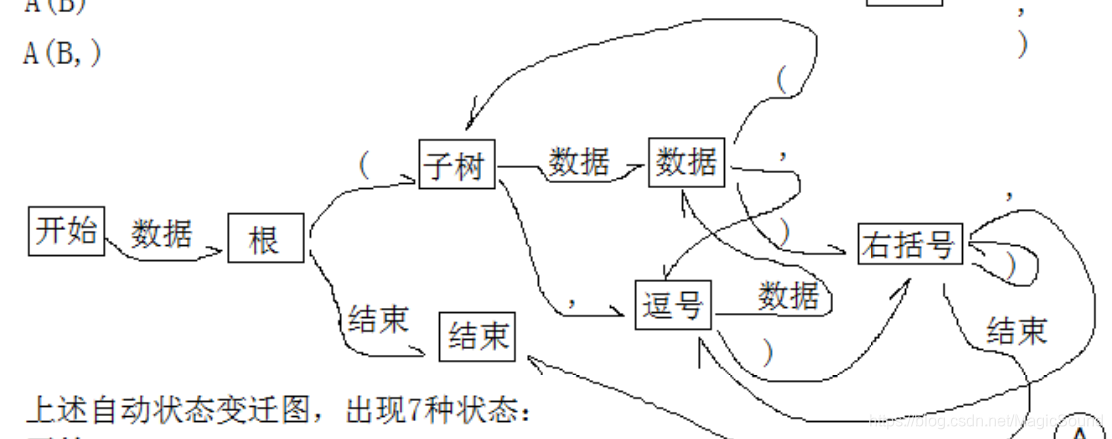
此时不进行括号失配等特殊问题的考虑，状态变迁图先在理想正确情况下完成基础形式，之后再慢慢完善
状态变迁图完成后，程序的基本框架就可以写出来了
共有开始，跟，子树，数据，逗号，右括号，结束七种状态

typedef struct BTREE_ARG {
	int status;
	boolean ok;
	boolean finished;
	int index;
	B_TREE *root;
}BTREE_ARG;

创建一个树的结构体，用于记录状态，是否有错，是否结束，当前下标。
整体思路是根据当前获取的字符，所处状态，作出对应的操作与状态变迁。

对于不同状态不同操作，以前用的办法是if else不断判断，或者switch case判断
此次可以用以指向函数的指针为元素的数组进行操作，因为不同状态是基于1~7数组define形成，对应状态的操作可以表示为数组对应下标。

typedef void (*dealFun)(BTREE_ARG *arg, int ch);
const dealFun functions[] = {
	NULL,
	dealBTreeBegin,
	dealBTreeRoot,
	dealBTreeSubTree,
	dealBTreeData,
	dealBTreeComma,
	dealBTreeRightBk,
	dealBTreeEnd,
};

不同状态函数内部操作都是类似的，根据获取的不同字符进行细节操作，例如

static void dealBTreeData(BTREE_ARG *arg, int ch) {
	if ('(' == ch) {
		dealLeftBracket(arg);
	} else if (',' == ch) {
		dealComma(arg);
	} else if (')' == ch) {
		dealRightBracket(arg);
	} else {
		arg->ok = FALSE;
	}
}

那么状态函数就不在赘述，都是一样的，重点是细节函数。
到了具体思考每个符号操作的时候，首先对于所有细节函数

	arg->status = ……;
	arg->index++;

状态变更和字符串下标增加是必须每个函数都有的。
经过思考，每个字符的操作如下：
根数据：生成节点并存储到根数据
左括号：左括号的前一个数据入栈，并且下一数据为左孩子
数据：生成节点，依据是左（右）孩子，读出栈顶数据，给左（右）孩子赋值
逗号：下一数据是右孩子（留存一个问题是多个逗号怎么判断）
右括号：遇到右括号说明一个二叉树生成完成，出栈即可

总结下来有几个问题：
①左右孩子如何判断
②堆栈如何生成
左右孩子问题在树结构体中新增一个实例boolean whichChild;
堆栈用于存储指针，新建堆栈还需要堆栈的容量（探树的深度）
树的深度实际就是最多同时存在的“编辑中”的节点。
寻找容量额外一个函数完成：

static int getStackDeep(const char *str) {
	int index;
	int match = 0;
	int maxMatch = 0;

	for (index = 0; match >= 0 && str[index]; index++) {
		if ('(' == str[index]) {
			++match;
			maxMatch = maxMatch < match ? match : maxMatch;
		} else if (')' == str[index]) {
			--match;
			if (match < 0) {
				return RIGHT_BRACKET_TOO_MUCH;
			}
		}
	}

	return match == 0 ? maxMatch : LEFT_BRACKET_TOO_MUCH;
}

遇左括号对数加一，右括号对数减一，有一个最大对数记录，最后return对数为0即数据正常，不为0则左括号过多
总结下树的结构体需要更新：

typedef struct BTREE_ARG {
	int status;
	boolean ok;
	boolean finished;
	int index;
	boolean whichChild;
	B_TREE *root;
	B_TREE *tmp;
	MEC_STACK *stack;
}BTREE_ARG;

具体函数细节：
逗号：

static void dealComma(BTREE_ARG *arg) {
	B_TREE *parent = NULL;

	parent = readTop(arg->stack);
	if (parent->right != NULL) {
		arg->ok = FALSE;

		return;
	}

	arg->whichChild = RIGHT_CHILD;
	arg->status = BTREE_STATUS_COMMA;
	arg->index++;
}

逗号函数有个拒绝多个逗号的细节：当栈顶节点的右孩子不为NULL（即赋过值），说明该逗号不合理

右括号：

static void dealRightBracket(BTREE_ARG *arg) {
	pop(arg->stack);

	arg->status = BTREE_STATUS_RIGHTBK;
	arg->index++;
}

直接出栈即可

左括号：

static void dealLeftBracket(BTREE_ARG *arg) {
	arg->whichChild = LEFT_CHILD;
	push(arg->stack, arg->tmp);

	arg->status = BTREE_STATUS_SUB_TREE;
	arg->index++;
}

改左孩子标记，数据入栈

跟：

static void dealRoot(BTREE_ARG *arg, int ch) {
	arg->root = (B_TREE *) calloc(sizeof(B_TREE), 1);
	arg->root->data = ch;
	arg->tmp = arg->root;
	
	arg->status = BTREE_STATUS_ROOT;
	arg->index++;
}

跟数据和其他数据需要分开处理

数据：

static void dealNode(BTREE_ARG *arg, int ch) {
	B_TREE *parent = NULL;

	arg->tmp = (B_TREE *) calloc(sizeof(B_TREE), 1);
	arg->tmp->data = ch;

	parent = readTop(arg->stack);
	if (LEFT_CHILD == arg->whichChild) {
		parent->left = arg->tmp;
	} else {
		parent->right = arg->tmp;
	}

	arg->status = BTREE_STATUS_DATA;
	arg->index++;
}

遇到数据先生成节点，读栈顶为父节点，给左（右）孩子赋值

细节函数完成，进行一次整合的create函数：

boolean createBTree(const char *str, B_TREE **root) {
	BTREE_ARG arg = {
		BTREE_STATUS_BEGIN,		// int status;
		TRUE,					// boolean ok;
		FALSE,					// boolean finished;
		0,						// int index;
		LEFT_CHILD,				// boolean whichChild;
		NULL,					// B_TREE *root;
		NULL,					// B_TREE *tmp;
		NULL, 					// MEC_STACK *stack;
	};
	int ch;
	int stackCapacity;

	if (NULL == str || NULL == root || NULL != *root) {
		return FALSE;
	}
	stackCapacity = getStackDeep(str);
	if (stackCapacity < 0) {
		arg.ok = FALSE;
	} else {
		initStack(&arg.stack, stackCapacity);
	}


	while (arg.ok && !arg.finished) {
		arg.index += skipBlank(str + arg.index);
		ch = str[arg.index];

		functions[arg.status](&arg, ch);
	}

	destoryStack(&arg.stack);

	if (arg.ok) {
		*root = arg.root;
	} else {
		destoryBTree(arg.root);
	}

	return arg.ok;
}