查找与排序

排序

冒泡排序
时间复杂度：
平均情况：O(n^2)
最好情况：O(n)
最坏情况：O(n^2)
空间复杂度：O(1)
稳定性：稳定

for(int i=0;i<n;i++){
  for(int j=0;j<n-i-1;j++){
    if(list[j+1]>list[j]){
      int tmp=list[j];
      list[j]=list[j+1];
      list[j+1]=tmp;
    }
  }
}

实际上，上面的实现代码时间复杂度始终为O(n^2)，如果一组数字一开始就完全有序的话，上述代买就完全没有必要全部遍历，所以每次遍历一遍列表，同时记住交换元素的位置，若此次遍历无元素交换，则直接停止。

快速排序
时间复杂度：
平均情况：O(nlogn)
最好情况：O(nlong)
最坏情况：O(n^2)
空间复杂度：
平均情况：O(logn)
最好情况：O(logn)
最坏情况：O(n)
稳定性：不稳定

void quickSort(int arr[], int low, int high)
{
    int first = low;
    int last  = high;
    int key = arr[first];//基准 
    if(low >= high)
        return;
    while(first < last)
    {
        while(first < last && arr[last] > key)
        {
            last--;
        }
        arr[first] = arr[last];
        while(first < last && arr[first] < key)
        {
            first++;
        }
        arr[last] = arr[first];
    }
    arr[first] = key;
    quickSort(arr, low, first-1);
    quickSort(arr, first+1, high);
}

直接选择排序
时间复杂度：
平均情况：O(n^2)
最好情况：O(n^2)
最坏情况：O(n^2)
空间复杂度：O(1)
稳定性：不稳定
在待排序列表中找到最小（大）的元素，把它放在起始位置作为已排序序列，然后，再从剩余待排序序列中找到最小（大）的元素放在已排序序列的末尾，以此类推，直至完毕。

    for(i=0;i<n-1;i++){ 
        for (j=i+1;j<n;j++){
            if(a[i]>a[j])  //如果前一个数比后一个数大，则利用中间变量t实现两值互换
            {
                int t=a[i];
                a[i]=a[j];
                a[j]=t;
            }
        }
    } 

堆排序
时间复杂度：初始化堆O(n)，交换元素后调整堆O(nlogn)
平均情况：O(nlogn)
最好情况：O(nlogn)
最坏情况：O(nlogn)
空间复杂度：O(1)
稳定性：不稳定
过程可以分为建堆和排序。堆排序不需要额外的空间，属于内部排序

直接插入排序
时间复杂度：

平均情况：O(n^2)
最好情况：O(n)
最坏情况：O(n^2)
空间复杂度：O(1)
稳定性：稳定

    for(i=1;i<n;i++)
    {
        if(a[i]<a[i-1])
        {
            int temp=a[i];
            for(j=i-1;j>=0 && a[j]>temp;j--)
                a[j+1]=a[j];
            a[j+1]=temp;
        }
    }

希尔排序
时间复杂度：
平均情况：O(nlogn~n^2)
最好情况：O(n^1.3)
最坏情况：O(n^2)
空间复杂度：O(1)
稳定性：不稳定
将待排序列表按下标的一定增量分组，各组内进行直接插入排序；随着增量的越来越小，每组所包含的数字序列越来越多，当增量减至1时，整个序列被分成一个组，排序完成。

归并排序
时间复杂度：
平均情况：O(nlogn)
最好情况：O(nlogn)
最坏情况：O(nlogn)
空间复杂度：O(n)
稳定性：稳定

基数排序
基数排序时间复杂度：O(nlog®m)，其中r为所采取的基数，而m为堆数
基数排序可以分为最高位优先法（MSD）和最低位优先（LSD）
LSD首先按各位放入不同的桶中，然后将所有桶中按队列出队组合，再按十位重复上述步骤，适用于位数小的数列，如果位数多的话，使用MSD的效率会比较好。MSD的方式与LSD相反，是由高位数为基底开始进行分配，但在分配之后并不马上合并回一个数组中，而是在每个“桶子”中建立“子桶”，将每个桶子中的数值按照下一数位的值分配到“子桶”中。在进行完最低位数的分配后再合并回单一的数组中。
LSD：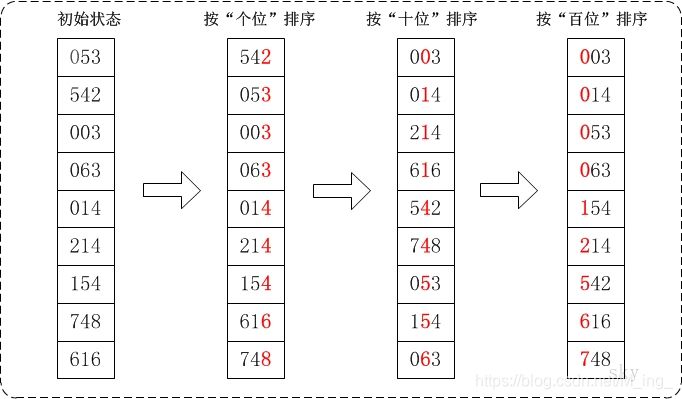

查询

查找算法分类：
　　1）静态查找和动态查找；
　　　　注：静态或者动态都是针对查找表而言的。动态表指查找表中有删除和插入操作的表。
　　2）无序查找和有序查找。
　　　　无序查找：被查找数列有序无序均可
　　　　有序查找：被查找数列必须为有序数列
顺序查找
顺序查找适合于存储结构为顺序存储或链接存储的线性表。
时间复杂度：O(n)
平均查找长度：ASL = (n+1)/2
二分查找（折半查找）
二分查找属于有序查找，需要被查找序列有序
最坏情况下，关键词比较次数为log2(n+1)，且期望时间复杂度为O(log2n)

int BinarySearch1(int a[], int value, int n)
{
    int low, high, mid;
    low = 0;
    high = n-1;
    while(low<=high)
    {
        mid = (low+high)/2;
        if(a[mid]==value)
            return mid;
        if(a[mid]>value)
            high = mid-1;
        if(a[mid]<value)
            low = mid+1;
    }
    return -1;
}

查找算法还是有二叉树，B树，B+树，hash等等…累了累了