目录
1.树概念及结构
1.1概念
树是一种非线性的结构,因为树会出现分岔,在逻辑上不是完全连续的。
虽然现实的树,根是在地下,但我们程序里的二叉树,最上面的节点,称为根。
对于接下来的节点,来说,每个节点又是一颗新的树(结构类似),即子树(可以借助数学上的子集来理解,虽然还有不同,但类似)
虽然树可以通过循坏实现,但在定义上树就是递归定义。
注意,一颗树里的子树不能互相有交集,否则就不是树了。
1.2树的基本概念
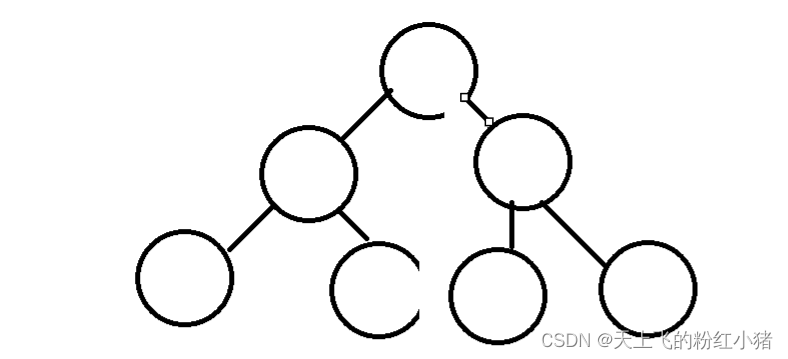
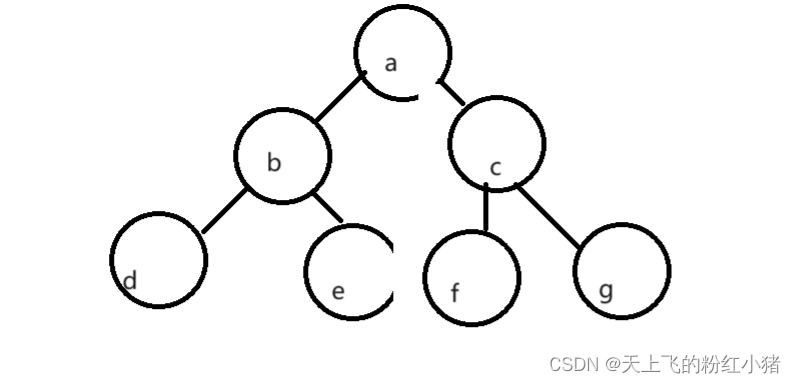
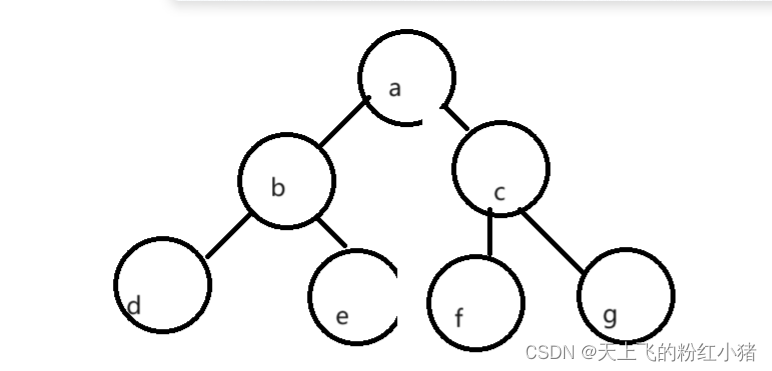
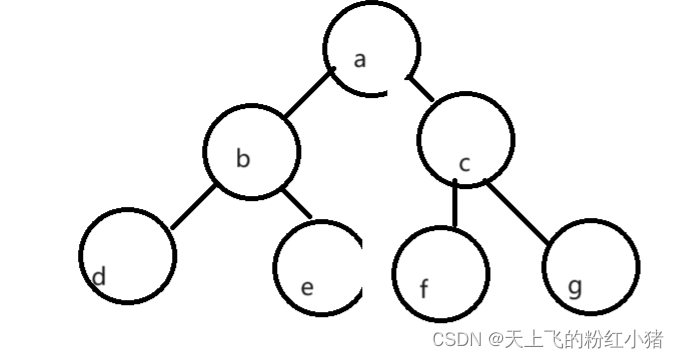
1.(节点的度):一个节点的子树个数,比如a有b树和c树,那么a节点的度就是2
2.叶节点:没有子树(子节点)的节点称为叶节点,也就是度为0的节点,如d、e、f、g。
3.分支节点:度不为0的节点,如b、c
4.父节点:a是b、c的父节点,b是d、e的父节点
5.子节点:b、c是a的子节点,d、e是b的子节点
6.兄弟节点:b、c的父节点是a,b是c的兄弟节点,c是b的兄弟节点
7.树的度:一个树中每个节点的度都可能不一样,最大的度即为树的度
8.节点的层次:根所在的就是第一层,然后依次往下,b、c是第二层
9.树的高度、深度:节点的最大层次,如上图就是3
10.堂兄弟节点:d和f就是堂兄弟节点
11.节点祖先:b是d、e的祖先,a是所有节点的祖先
12.子孙:d、e是b的子孙,所有节点都是a的子孙
13.森林:好多个没有交集的树的集合,称为森林。
1.3树的表示
typedef int DataType; struct Node { struct *firstChild;//第一个孩子节点 struct Node* nextBrother;//同层的下一个兄弟节点 DataType data; }; 这是比较经典的孩子兄弟表示法,类似的 还有双亲表示、孩子表示、孩子双亲。
2.二叉树
2.1二叉树基本概念
在平时,还是二叉树居多,而二叉树也分很多。
一颗二叉树的最基本定义:节点的有限集合,这个集合可能为空,也可以由一个根加2个子树,即左树和右数,
这个树就是比较经典的二叉树
二叉树不能有度大于2的节点,每个节点的子树都分左树和右树,且顺序不能变(假如一个节点有一个子树,但他是放在右树的指针上的,那他就是右树,不能称为左树)
2.2特殊的二叉树
第一个。满二叉树,每一层,节点都是满的,除了最后一层的叶节点,每个节点都是度为2的节点。不会出现哪个地方缺一个节点。
且假如满二叉树有k层,那么节点总数就是2^k-1
第二个,完全二叉树,相比满二茶树,完全二叉树要么是度为2的节点,要么就是度为0的节点,且除了最后一层之外,前面层节点都是满二叉树状态,最后一层可以不满,但是顺序必须是从左到右
2.3二叉树性质
1.假如,根节点层数为1,则非空二叉树的i层上最多有2^(i-1)个节点
2.假如根节点层数为1,则深度为h的二叉树的最大节点数是2^h-1,这个可以理解为最大节点数的情况,就是满二叉树。
3.对任何一刻二叉树,如果度为0的叶节点数有n0,度为2的有n2个则n0=n2+1
4.假如根节点层数为1,有n个节点的满二叉树的深度,h=log2(n+1)
5.对于有n个节点的完全二叉树,若从上到下,左到右顺序的数组顺序排列,从0开始,第i个节点:
5.1.若i>0,i节点的父节点:(i-1)/2,i=0,无父节点
5.2. 若2*i+1<n,i的左孩子是2*i+1,否则无左孩子;
5.3若2*i+2<n,i的右孩子:2*i+2,否则无右孩子
2.4二叉树结构
分为顺序结构和链式结构。
顺序结构就是数组存储,一般用来表示完全二叉树或满二叉树,因为这两个特殊的树不会有浪费空间的情况。
链式结构,分二叉链和三叉链。二叉链就是数据、左孩子指针、右孩子指针,三叉链多个父节点指针。
3.二叉树顺序结构实现
顺序结构一般用是来存储完全二叉树,而对我们来说,完全二叉树,最大的作用就是堆,
堆也是一种完全二叉树。堆的的某个非根节点,总是不大于(大堆)或者不小于(小堆)其父节点。
3.1头文件
#pragma once #include<stdio.h> #include<stdlib.h> #include<assert.h> #include<stdbool.h> typedef int HPDataType; //方便改数据类型 typedef struct Heap { HPDataType* a; int size;//有效数组个数 int capacity;//数组大小 }HP; //用数组存储,节点的结构和顺序表类似 //堆的初始化 void HeapInit(HP* php); //销毁 void HeapDestory(HP* php); //插入 void HeapPush(HP* php, HPDataType x); //删除 void HeapPop(HP* php); //获取堆顶元素 HPDataType HeapTop(HP* php); 获取堆的大小 int HeapSize(HP* php); //判断堆是否为空 bool HeapEmpty(HP* php); //堆的一种应用,堆排序 void Heapsort(int* a, int size);3.2堆的具体实现
3.2.1初始化
void HeapInit(HP* php) { assert(php); php->a = NULL; php->capacity = 0; php->size = 0; } 断言空指针 数组指针置空,其他都置03.2.2销毁
void HeapDestory(HP* php) { assert(php); free(php->a); php->a = NULL; php->size = 0; php->capacity = 0; } 断言空指针 释放数组空间 数组指针置0,size和capacity都置03.2.3简易交换函数(方便调用)
void Swap(HPDataType*a,HPDataType*b) { HPDataType tmp = *a; *a = *b; *b = tmp; } 就是交换数据的3.2.4向上调整 (大堆版)
void AdjustUp(HPDataType * a, int child) { assert(a); int parent = (child - 1) / 2; while (1) { if (a[child] > a[parent]) { Swap(&a[child], &a[parent]); child = parent; parent = (parent - 1) / 2; } else { break; } } } 断言空指针 parent就是当前child节点的父节点 while循坏中,进行判断,只要child节点比父节点大,就进行交换,然后继续向上, child指向parent,parent指向新的父节点,一旦相等或小于,就停止循坏。 如果要建小堆,就判断child节点比父节点小即可3.2.5数据插入
void HeapPush(HP* php, HPDataType x) { assert(php); if (php->size == php->capacity) { int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2; php->capacity = newcapacity; HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * php->capacity); if (tmp == NULL) { perror("realloc fail"); exit(-1); } php->a = tmp; } php->a[php->size] = x; php->size++; AdjustUp(php->a,php->size-1); } 断言空指针 进行扩容判断,如果size==capacity,因为size是有效数据个数,size就是下一个待存储数据的下标 而数组下标是从0开始,因此这时数组已经满了。需要扩容 定义newcapacity,如果本身是空堆,就赋予4个数据大小,否则就扩容2倍。 这里不多说,扩容是顺序表的重点内容。 扩容完成后,我们把值往size位置上放即可,size记得++ 然后调用向上调整的函数,这样就可以把这个新加的数,通过向上调整,放在合适(即让整个堆 继续满足大堆或小堆)的地方3.2.6向下调整(重点!)大堆版
void AdjustDown(HPDataType *a, int size, int parent) { int child = parent * 2 + 1; while (child < size) { if (child+1<size &&a[child+1] > a[child]) { child++; } if (a[child] > a[parent]) { Swap(&a[child], &a[parent]); parent = child; child = parent * 2 + 1; } else { break; } } } child是parent节点的左孩子 while循坏条件,用child<size即可,size是最后一个有效下标的下一个下标 判断左孩子大还是右孩子大(前提是有右孩子),我们这里是建大堆 那么只要把当前节点的最大的孩子节点跟当前节点判断大小, 假如孩子节点大于父节点,那么交换,满足大堆条件,然后继续往下, parent指向这个当前的孩子节点,child指向当前节点的孩子节点的左孩子节点 如果孩子节点小于等于父节点,则停止循坏,或者已经到了数组的最后一个下标 注意,一次向下调整,只会沿着一条路往下走,这点在用向下调整造大堆时有用3.2.7返回堆顶元素
HPDataType HeapTop(HP* php) { assert(php); assert(php->a); return php->a[0]; } 这个是返回堆顶元素的,因为是数组存储,我们直接返回0下标即可3.2.8删除堆顶元素
void HeapPop(HP* php) { assert(php); assert(php->size > 0); Swap(&php->a[0], &php->a[php->size - 1]); php->size--; AdjustDown(php->a, php->size, 0); } 我们把堆顶和数组后一个元素交换,这样顺序表尾删就只要size-- 然后对堆顶下标进行一次向下调整,然堆顶元素放在合适的位置(满足大堆或小堆)3.2.9获取堆的数据数量
int HeapSize(HP* php) { assert(php); return php->size; } 大小,直接返回size即可3.2.10判断堆是否为空
bool HeapEmpty(HP* php) { assert(php); return php->size == 0; } 判断空指针 bool类型,返回一个关系表达式即可3.2.11堆排序
void Heapsort(int* a, int size) { assert(a); for (int i = ((size-1)-1)/2; i >=0; i--) { AdjustDown(a, size,i); } int end = size - 1; while (end > 0) { Swap(&a[0], &a[end]); AdjustDown(a, end, 0); end--; } } 断言空指针 堆排序的前提是,我们要先建一个堆,因为我们要对一个数据进行排序, 假如是升序,那么我们要把数据放入大堆中,这样堆顶必是最大的数。 我们先说如何建堆,建完怎么排序,待会说 关于建堆,我们可以用向上调整算法和向下调整算法,但这里推荐用向下调整,为什么呢 ,我们要明白,完全二叉树或者满二叉树的结构,决定了最下面的层,节点数大概是最多的 如果是不是满二叉树,只是完全二叉树,那么向上和向下,差别不大,但是 如果是满二叉树,向下调整是从最后一个分支节点开始建堆,而向上调整是从最后一个节点开始建堆 最后一层的节点数大概占整个数的50%左右,所以两者在满二叉树或接近满二叉树的树上,有很大的区别 向下调整我们从最后一个分支节点开始向下调整。 说完建堆,我们看如何排序 end是最后一个有效数据的下标 我们先将堆顶数据和最后一个数据交换,(第一次堆顶数据是整个堆最大的 ),再让堆顶进行向下调整,然后end--(end是已经排好的了) 接下来重复操作,向下调整完,堆顶数据是一个次大的数据,再下一次就是次次大 这样就可以把大的数据排到最后,直到end=0,说明已经此时已经排好了。3.3堆例题
top-k问题,求数据中前k个最大或最小的元素
如果是前k个最大,我们建k大小的小堆,如果最小,则是大堆void CreateNDate() { // 造数据 int n = 10000; srand(time(0)); const char* file = "data.txt"; FILE* fin = fopen(file, "w"); if (fin == NULL) { perror("fopen error"); return; } for (size_t i = 0; i < n; ++i) { int x = rand() % 1000000; fprintf(fin, "%d\n", x); } fclose(fin); } //这个造一堆随机数,放在文件里 void PrintTopK(const char* file, int k) { FILE* fout = fopen(file, "r"); if (fout == NULL) { perror("fopen error"); return; } //引入文件 int* min = (int*)malloc(sizeof(int) * k); if (min== NULL) { perror("malloc error"); return; } //创建k大小的数组 for (int i = 0; i < k; i++) { fscanf(fout, "%d", min[i]); AdjustUp(min, i); } //把k个数据先放入数组,通过向上调整的方式,造一个小堆 int x = 0; while (fscanf(fout, "%d", &x) != EOF) { if (x > min[0]) { min[0] = x; AdjustDown(min, k, 0); } } //接下来,把剩下的数据都读出来,因为我们是小堆,堆顶数据是堆里最小的 //堆顶数据和读出来的数据比较,大于堆顶数据的变成堆顶数据,然后向下调整 //保证堆顶数据是堆里最小的 //这样就能把k个最大的数据找出来 for (int i = 0; i < k; i++) { printf("%d", min[i]); } //打印 printf("\n"); fclose(fout); }
4.二叉树的链式结构
链式结构是指将二叉树以指针的形式链接,我们在这里采用左孩子和右孩子的链接方式,
在构建二叉树前,我们先学习如何遍历一个二叉树,因为构建二叉树的时候本质上也是一种遍历。
遍历就是对二叉树的每个节点进行一次访问。
遍历有4种方式,前序、中序、后序、中序
4.1前序遍历
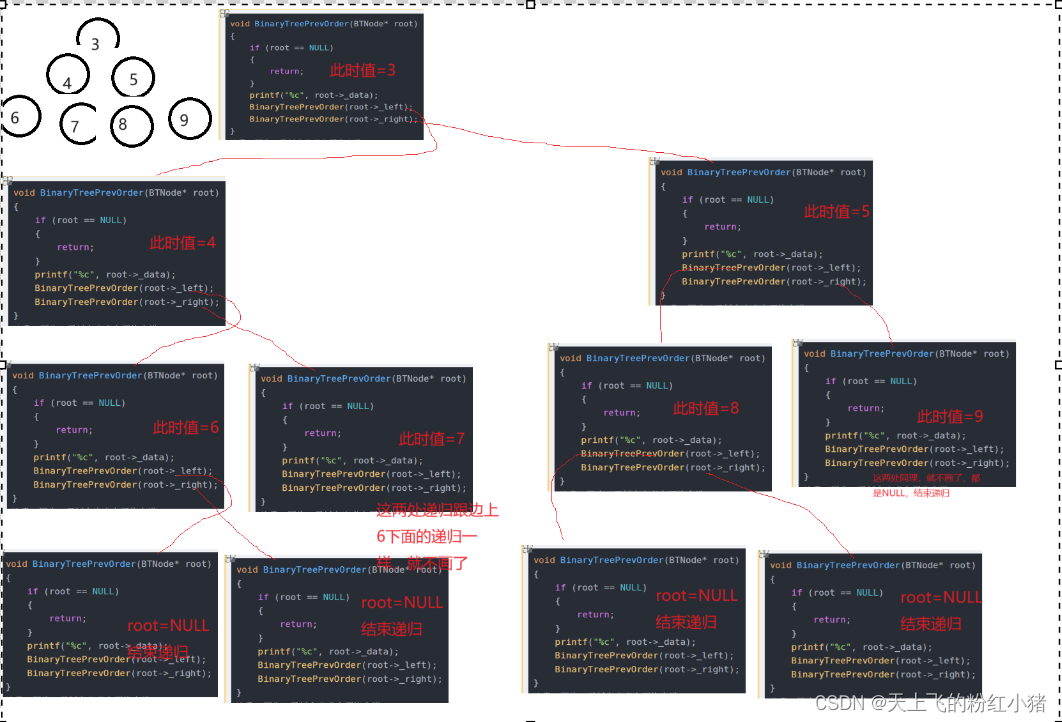
void BinaryTreePrevOrder(BTNode* root) { if (root == NULL) { return; } printf("%c", root->_data); BinaryTreePrevOrder(root->_left); BinaryTreePrevOrder(root->_right); } 注意,因为二叉树在定义上严格来说 是递归定义的,这里遍历我们也采用递归的形式 要注意,我们前序遍历,一旦遇到一个节点,就会打印当前节点的数据 是从根节点开始打印的
4.2中序遍历
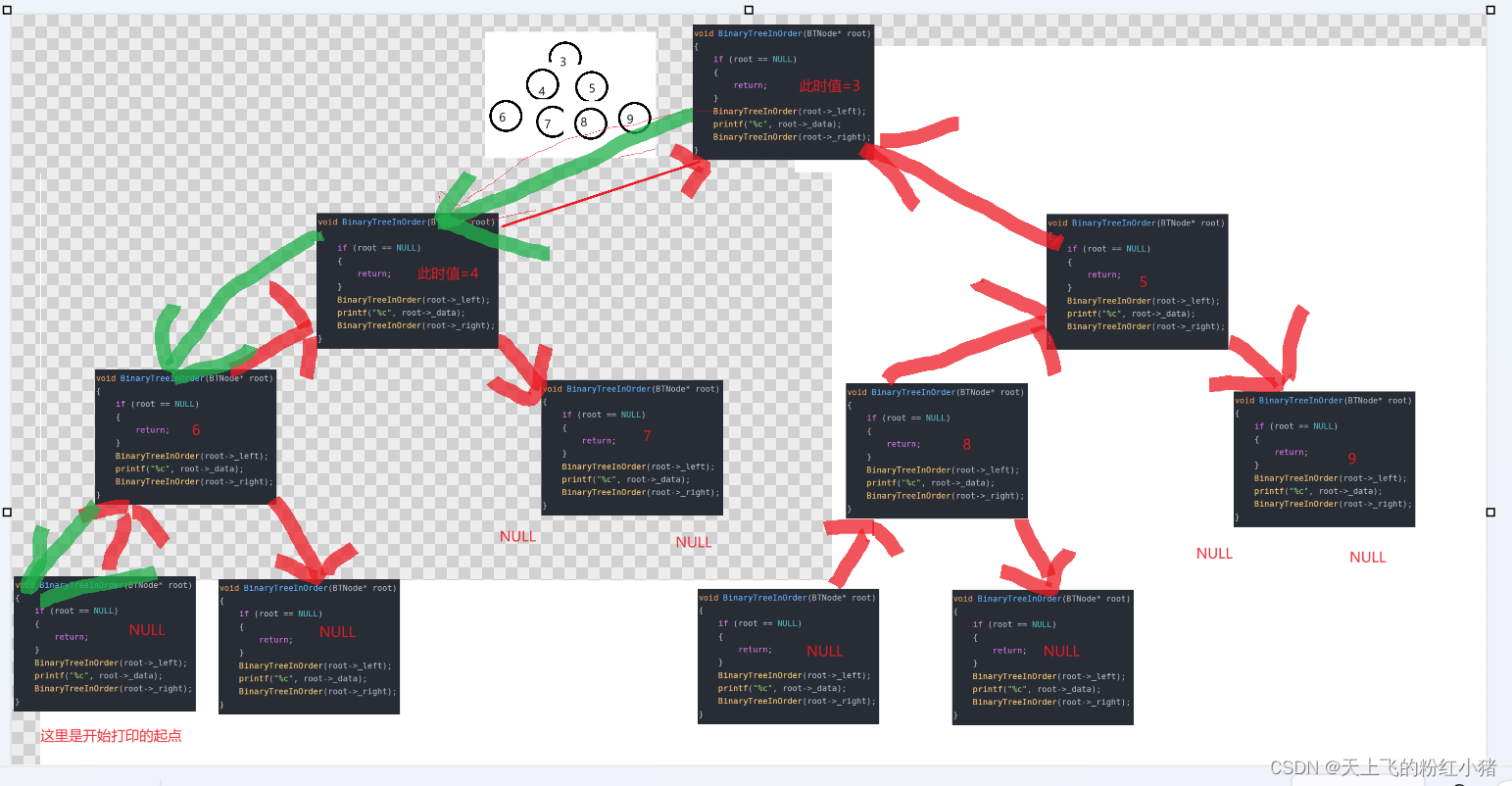
void BinaryTreeInOrder(BTNode* root) { if (root == NULL) { return; } BinaryTreeInOrder(root->_left); printf("%c", root->_data); BinaryTreeInOrder(root->_right); } 中序遍历会先遍历到最左边,才开始打印数据
绿色是遍历的路径,当遍历到最左边,遇到NULL返回之后,才会开始打印数据,之后遍历打印的顺序就是红色箭头
4.3后序遍历
void BinaryTreePostOrder(BTNode* root) { if (root == NULL) { return; } BinaryTreePostOrder(root->_left); BinaryTreePostOrder(root->_right); printf("%c", root->_data); } 这里不多做解释,都差不多4.4层序遍历
void LevelOrder(BTNode* root) { Queue q; QueueInit(&q); //创建队列,初始化队列 if (root) { QueuePush(&q, root); } //将当前二叉树根节点的地址入队 int levelsize = 1; //记录当前层有多少个节点 //因为第一层肯定是1个,所以默认1 while (!QueueEmpty(&q)) { // 直到队列为空才结束循坏,因为每个节点都遍历过了 while (levelsize--) { BTNode* front = QueueFront(&q); printf("%c ", front->_data); QueuePop(&q); //先创建一个二叉树节点,接受队列里的节点地址 //打印节点数据,然后出队 if (front->_left) { QueuePush(&q, front->_left); } if (front->_right) { QueuePush(&q, front->_right); } //出队后,把当前节点的孩子按左孩子右孩子的顺序入队, } //这里用levelsize--,因为levelsize是当前层的节点个数 printf("\n"); levelsize = QueueSize(&q); //这里就是精华了,怎么判断当前层的节点数呢,我们可以看到 //每次出队后都会把当前节点的孩子入队,那一层的最后一个节点出队后 //把他的孩子入队后,那么队列里面此时存的是不是正好就是下一层所有的节点 //因为从一层的最左边到最右边,每个节点都会出队自己,入队自己的孩子 } printf("\n"); QueueDestrory(&q); //因为此时,队列里的数据个数,就是二叉树下一层的节点个数 } 这里需要用到队列,利用队列的先进先出实现,(栈也可以,我们这采用队列)4.5二叉树构建和销毁
接下来,我们先借助一道例题,学习,如何借助已有的前序\中序\后序\层序的数据,构建一个二叉树
#include <stdio.h> #include<stdlib.h> typedef struct BTreeNode { int val;//数据 struct BTreeNode*left;//指向左孩子 struct BTreeNode*right;//指向右孩子 }BTree; //这是链接二叉树的节点结构 void TreeInOrder(BTree * root) { if(root==NULL)return; TreeInOrder(root->left); printf("%c ",root->val); TreeInOrder(root->right); } //这是中序遍历(之前讲了) BTree* Treecreate(char *a,int *pi) { if(a[*pi]=='#') { (*pi)++; return NULL; } BTree*root=(BTree*)malloc(sizeof(BTree)); root->val=a[*pi]; (*pi)++; root->left=Treecreate(a, pi); root->right=Treecreate(a, pi); //这里是利用返回值是地址类型,从而从零创建一个二叉树 return root; } //这是核心的构建二叉树 //题目给的是前序遍历的数组,那么我们先模拟前序遍历的方式 //前序遍历是先访问当前节点的数据再递归左孩子右孩子 //那么,按照顺序,数组里的值应该是正正好匹配的,所以直接把 //值赋值过去就好,下标用指针,因为我们是按顺序遍历数组的下标 //用形参会出现遍历了同一个数据下标的情况 //注意,遇到#说明是遇到NULL了,所以下标++的同时,返回 //NULL即可 int main() { char a[100]={0}; scanf("%s",a); int i=0; BTree*root=Treecreate(a, &i); TreeInOrder(root); return 0; }销毁如下
void BinaryTreeDestory(BTNode*root) { if (root== NULL) { return; } BinaryTreeDestory(root->_left); BinaryTreeDestory(root->_right); free(root); root = NULL; } 为了防止找不到节点了,我们要先遍历到最后一个节点开始free4.6节点个数
int BinaryTreeSize(BTNode* root) { if (root == NULL) { return 0; } return BinaryTreeSize(root->_left) +1+ BinaryTreeSize(root->_right); } 以中序遍历的方式,计算访问过的节点个数4.7叶节点个数
int BinaryTreeLeafSize(BTNode* root) { if (root == NULL) { return 0; } if (root->_left==NULL && root->_right==NULL) { return 1; } return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right); } 注意,我们要计算的是叶节点,叶节点就是孩子都是NULL的 //那么,把之前计算节点个数的代码稍微改下 //加1不放在下面的return中,而是放在if条件中,满足叶子条件的才能+14.8第k层节点个数
int BinaryTreeLeafKSize(BTNode* root,int k) { if (root == NULL)return 0; if (k == 1 ) { return 1; } return BinaryTreeLeafKSize(root->_left, k - 1) + BinaryTreeLeafKSize(root->_right, k - 1); } 第k层,那么每次递归,都把k-1的值递归给左孩子和右孩子 //如果k=1,说明已经递归到了第k层4.9查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x) { if (root == NULL)return NULL; if (root->_data == x)return root; BTNode* newnode= BinaryTreeFind(root->_left, x); if (newnode)return newnode; else return BinaryTreeFind(root->_right, x); } 本质就是前序遍历 //每次遍历的都会返回一个地址,如果该节点的左树或右树找到了 x,就会返回地址4.10判断是否是完全二叉树
bool TreeComplete(BTNode* root) { Queue q; QueueInit(&q); if (root) { QueuePush(&q, root); } //利用队列,先将根节点入队 while (!QueueEmpty(&q)) { BTNode* front = QueueFront(&q); QueuePop(&q); if (front==NULL)break; QueuePush(&q, front->_left); QueuePush(&q, front->_right); } //直到队列为空,否则,获取队头的二叉树节点地址,再出队,判断获取的二叉树节点地址是不是空,不是 //空,就继续把获取的二叉树节点的孩子入队,跟层序一样 //如果遇到了NULL,就退出循坏 while (!QueueEmpty(&q)) { BTNode* front = QueueFront(&q); QueuePop(&q); if (front) { QueueDestrory(&q); return false; } } //如果是完全二叉树,NULL的后面也必定都是NULL,如果遇到了非NULL,说明不是完全二叉树 QueueDestrory(&q); return true; }4.11例题
4.11.1单值二叉树
bool isUnivalTree(struct TreeNode* root) { if(root==NULL)return true; if(root->left && root->left->val != root->val) { return false; } if(root->right && root->right->val!=root->val) { return false; } return isUnivalTree(root->left) && isUnivalTree(root->right); } 很简单,每个节点值相等,说明每个节点跟自己的孩子节点值也都相等 //那么我们遍历每个节点,如果孩子节点不是空,且孩子节点值跟父节点值不等 //说明就不是单值二叉树,返回false即可,因为return那是&&,只要有一个false //最终定是返回一个false4.11.2相同的树
bool isSameTree(struct TreeNode* p, struct TreeNode* q) { if(p==NULL && q==NULL)return true; if(p==NULL || q==NULL)return false; if(p->val!=q->val)return false; return isSameTree(p->left,q->left) && isSameTree(p->right,q->right); } 相同的树,是结构和值都要相等 //那么,利用&&连接返回值,然后判断false和true情况即可 //如果同时都==NULL,说明已经遍历到了最后,那么返回true即可 //但如果是一个为空,另一个非空,则说明结构不相等,返回false //如果val不相等,说明值不相等,也是false //因为是&&,只要有一个false,最后整体递归结束,返回的值定是false4.11.3对称二叉树
bool _isSymmetric(struct TreeNode* root1,struct TreeNode*root2) { if(!root1 && !root2) { return true; } if(!root1 || !root2) { return false; } if(root1->val!=root2->val) { return false; } return _isSymmetric(root1->left,root2->right) && _isSymmetric(root1->right,root2->left); } bool isSymmetric(struct TreeNode* root) { return _isSymmetric(root->left,root->right); } //从根节点的左树和右树开始 //利用子函数,判断两个树的左树是否相等,右树是否相等,即可判断整个树是否是对称的4.11.4另一棵树的子树
bool isSameTree(struct TreeNode*p ,struct TreeNode*q) { if(!p && ! q) { return true; } //如果都是空,结构相等,返回true if(p==NULL || q==NULL)return false; //结构不相等,返回false if(p&&q) { if(p->val!=q->val ||!isSameTree(p->left,q->left)) { return false; } } //判断,如果两个树的当前节点值不相等,或者两个树的左子树结构和值不相等 //就返回false if(p&&q) { if(p->val !=q->val ||!isSameTree(p->right,q->right)) { return false; } } //判断,如果两个树的当前节点值不相等,或者两个树的右子树结构和值不相等 //就返回false return true; //严格来说,前面的代码都是判断怎么样不相等,如果前面的都没触发,说明当前两颗树的结构 //和值都是相等的 } //子函数的判断,本质上就是判断结构和值是否相等,判断由下面函数第一次传进来 的节点作为两个树的根节点,判断这两棵树的结构和值是否相等 bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){ if(!root)return false; if(root->val==subRoot->val) { if(isSameTree(root,subRoot)) return true; } if(isSubtree(root->left,subRoot)) return true; if(isSubtree(root->right,subRoot)) return true; return false; } 因为我们不能确定是从root树的哪部分开始才是跟subroot树相等,我们会先进行判断 直到我们找到一个值跟subroot节点的根节点的值相等的,然后我们进行子函数的判断
5.补充
向下建堆是o(n),向上建堆是n*logn





















 385
385

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








