ZFNet: Visualizing and Understanding Convolutional Networks

最新推荐文章于 2020-08-24 16:16:32 发布

MTandHJ

最新推荐文章于 2020-08-24 16:16:32 发布

阅读量157

点赞数

分类专栏： neural networks

neural networks 专栏收录该内容

143 篇文章

订阅专栏

本文详细介绍了ZFNet的网络结构，并针对其输入输出尺寸的变化进行了具体说明。此外，还深入探讨了反卷积的过程及计算方法，旨在帮助读者理解如何通过补零操作实现特征图的逆向重建。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

- 论文结构
- 反卷积

ZFnet的创新点主要是在信号的“恢复”上面，什么样的输入会导致类似的输出，通过这个我们可以了解神经元对输入的敏感程度，比如这个神经元对图片的某一个位置很敏感，就像人的鼻子对气味敏感，于是我们也可以借此来探究这个网络各层次的功能，也能帮助我们改进网络。

论文结构

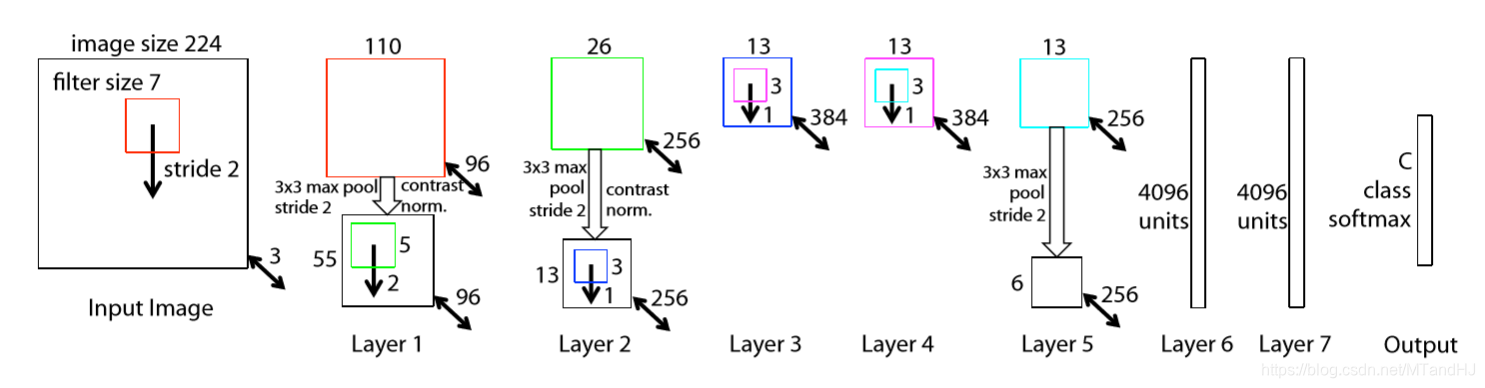
在这里插入图片描述

input: $\times 224 \times 224$ , filter size: 7, filter count: 96, stride: 2, padding: 1, 我觉得是要补一层零的，否则输出是109而不是110–>ReLU --> maxpool: size: $\times 3$ , stride: 2, 似乎这里也要补一层零，否则 $\lfloor \frac{110-3}{2}+1 \rfloor=54$ --> contrast normalized;
input: $96 \times 55 \times 55$ , filter size: 5, count: 256, stride: 2, padding: 0 --> ReLU --> maxpool: size: $\times 3$ , stride: 2, padding: 1–> contrast normlized;
input: $256 \times 13 \times 13$ , filter size: 3, count: 384, stride: 1, padding: 1 --> ReLU
input: $384 \times 13 \times 13$ , filter size: 3, count: 384, stride: 1, padding: 1 --> ReLU
input: $384 \times 13 \times 13$ , filter size: 3, count: 256, stride: 1, padding: 1 --> ReLU --> maxpool: size: 3, stride: 2, padding: 0 --> contrast normlized?
input: $6 * 6 * 256$ – > 4096 – > ReLU – > Dropout(0.5)
input: 4096 – > 4096 --> ReLU – > Dropout(0.5)
input: 4096 --> numclass …

反卷积

网上看了很多人关于反卷积的解释，但是还是云里雾里的.

先关于步长为1的，不补零的简单情况进行分析吧, 假设:

input: $\times i$ ,
kernel_size: $\times k$ ,
stride: 1,
padding: 0

此时输出的大小 $o$ 应当满足：
$\Rightarrow o = i-k+1$

现在，反卷积核大小依旧为 $k^{'} = k$ , 那么我们需要补零 $c^{'}$ 为多少才能使得反回去的特征大小为 $i$ .
即:
$\Rightarrow c'= k-1$
即我们要补零 $c^{'} = k - 1$ .

如果stride 不为1呢？设为 $s$ , 那么:
$\Rightarrow o = \frac{i-k}{s}+1$

按照别的博客的说话，需要在特征之间插入零那么:
$2 c^{'} + (s - 1) (o - 1) + o = k + s^{'} (i - 1)$

如果我们希望 $s^{'} = 1$ （至于为什么希望我不清楚）:
$c^{'} = k - 1$

如果还有补零 $p$ :
$i + 2 p = k + s (o - 1)$
但是回去的时候我们是不希望那个啥补零的，所以:
$2 c^{'} + (s - 1) (o - 1) + o = k + s^{'} (i - 1)$
不变,
如果 $s^{'} = 1$ , 结果为:
$c^{'} = k - p - 1$