目标
首先, 既然是变换, 那么就是从一个域到另一个域, 即如下:
f
(
x
)
=
∑
k
c
j
0
(
k
)
φ
j
0
,
k
(
x
)
+
∑
j
=
j
0
∞
∑
k
d
j
(
k
)
ψ
j
,
k
(
x
)
,
c
j
0
=
⟨
f
(
x
)
,
φ
j
0
,
k
(
x
)
⟩
,
d
j
=
⟨
f
(
x
)
,
ψ
j
,
k
(
x
)
⟩
.
f(x) = \sum_k c_{j_0} (k) \varphi_{j_0, k} (x) + \sum_{j=j_0}^{\infty} \sum_k d_j (k) \psi_{j, k}(x), \\ c_{j_0} = \langle f(x), \varphi_{j_0, k}(x) \rangle, \\ d_{j} = \langle f(x), \psi_{j, k}(x) \rangle. \\
f(x)=k∑cj0(k)φj0,k(x)+j=j0∑∞k∑dj(k)ψj,k(x),cj0=⟨f(x),φj0,k(x)⟩,dj=⟨f(x),ψj,k(x)⟩.
或者离散的情况:
f
(
x
)
=
1
N
[
∑
k
T
φ
(
j
0
,
k
)
φ
0
,
0
(
x
)
+
∑
j
=
j
0
J
−
1
∑
k
=
0
2
j
−
1
T
ψ
(
j
,
k
)
ψ
j
,
k
(
x
)
]
,
T
φ
(
j
0
,
k
)
=
⟨
f
(
x
)
,
φ
0
,
0
(
x
)
⟩
=
⟨
f
(
x
)
,
φ
j
0
,
k
(
x
)
⟩
=
1
N
∑
x
=
0
N
−
1
f
(
x
)
φ
j
0
,
k
∗
(
x
)
,
T
ψ
(
j
,
k
)
=
⟨
f
(
x
)
,
ψ
j
,
k
(
x
)
⟩
=
1
N
∑
x
=
0
N
−
1
f
(
x
)
ψ
j
,
k
∗
(
x
)
.
f(x) = \frac{1}{\sqrt{N}}[\sum_{k} T_{\varphi}(j_0, k) \varphi_{0, 0}(x) + \sum_{j=j_0}^{J-1}\sum_{k=0}^{2^j -1} T_{\psi}(j, k)\psi_{j, k}(x)], \\ T_{\varphi}(j_0, k) = \langle f(x), \varphi_{0, 0}(x) \rangle = \langle f(x),\varphi_{j_0, k} (x) \rangle = \frac{1}{\sqrt{N}} \sum_{x=0}^{N-1}f(x) \varphi_{j_0, k}^*(x), \\ T_{\psi}(j, k) = \langle f(x), \psi_{j, k}(x) \rangle = \frac{1}{\sqrt{N}} \sum_{x=0}^{N-1}f(x)\psi_{j, k}^* (x).
f(x)=N1[k∑Tφ(j0,k)φ0,0(x)+j=j0∑J−1k=0∑2j−1Tψ(j,k)ψj,k(x)],Tφ(j0,k)=⟨f(x),φ0,0(x)⟩=⟨f(x),φj0,k(x)⟩=N1x=0∑N−1f(x)φj0,k∗(x),Tψ(j,k)=⟨f(x),ψj,k(x)⟩=N1x=0∑N−1f(x)ψj,k∗(x).
通过上述的变换, 将 f f f变换至系数 c , d , T c, d, T c,d,T.
上面 { φ , ψ } \{\varphi, \psi\} {φ,ψ}共同组成正交基(或者书中定义的biorthogonal), 小波变换主要关注的就是下面几个目标:
- 迭代的构建正交基;
- φ \varphi φ能够提取低频信息, ψ \psi ψ能够提取高频信息;
- 快速变换, 即高效计算 c , d , T c, d, T c,d,T.
小波变换
Scaling Functions
小波变换的正交基是通过scaling functions引入的, 即如下的scaled and translated functions:
φ
j
,
k
(
x
)
=
2
j
/
2
φ
(
2
j
x
−
k
)
,
\varphi_{j, k}(x) = 2^{j/2}\varphi (2^j x - k), \\
φj,k(x)=2j/2φ(2jx−k),
定义 V j V_j Vj为固定 j j j平移 k k k所张成的空间 s p a n { φ j , k ∣ k ∈ Z } ‾ \overline{\mathrm{span}\{\varphi_{j, k}|k \in \mathbb{Z} \}} span{φj,k∣k∈Z}, 平方可积的scaling functions 同时需要满足下列的四个条件:
- ⟨ φ ( x ) , φ ( x − k ) ⟩ , k ≠ 0 \langle \varphi (x) , \varphi(x - k) \rangle, k \not = 0 ⟨φ(x),φ(x−k)⟩,k=0;
- V − ∞ ⊂ ⋯ ⊂ V − 1 ⊂ V 0 ⊂ V 2 ⋯ ⊂ V + ∞ V_{-\infty} \subset \cdots \subset V_{-1} \subset V_0 \subset V_2 \cdots \subset V_{+\infty} V−∞⊂⋯⊂V−1⊂V0⊂V2⋯⊂V+∞;
- f ( x ) = 0 f(x) = 0 f(x)=0是唯一属于任意空间 V V V的函数;
- V + ∞ = L 2 ( R ) V_{+\infty} = L^2(\mathbb{R}) V+∞=L2(R).
上面的4个条件的严格叙述还是看书上比较好, 不确定是否就是这样, 我没有看过原论文, 只是按照自己理解来.
对于平方可积函数, 可知:
⟨
φ
(
x
)
,
φ
(
x
−
k
)
⟩
,
⇒
⟨
φ
j
,
n
(
x
)
,
φ
j
,
n
(
x
−
k
)
⟩
,
k
≠
0.
\langle \varphi (x) , \varphi(x - k) \rangle, \Rightarrow \langle \varphi_{j,n} (x) , \varphi_{j, n}(x - k) \rangle, k \not = 0.
⟨φ(x),φ(x−k)⟩,⇒⟨φj,n(x),φj,n(x−k)⟩,k=0.
并由条件二可知:
φ
(
x
)
=
∑
k
∈
Z
h
φ
(
k
)
2
φ
(
2
x
−
k
)
,
\varphi (x) = \sum_{k \in \mathbb{Z}} h_{\varphi}(k) \sqrt{2} \varphi (2x - k),
φ(x)=k∈Z∑hφ(k)2φ(2x−k),
将
x
=
2
j
x
−
n
x = 2^j x - n
x=2jx−n代入可知,
φ
j
,
n
(
x
)
=
∑
k
∈
Z
h
φ
(
k
)
φ
j
,
2
n
+
k
(
x
)
.
\varphi_{j, n}(x) = \sum_{k \in \mathbb{Z}} h_{\varphi}(k)\varphi_{j, 2n+k}(x).
φj,n(x)=k∈Z∑hφ(k)φj,2n+k(x).
接着, 根据
⟨
φ
j
,
n
(
x
)
,
φ
j
,
n
(
x
−
n
′
)
⟩
=
0
,
n
′
≠
0
,
\langle \varphi_{j, n}(x), \varphi_{j, n}(x-n')\rangle = 0, n' \not = 0,
⟨φj,n(x),φj,n(x−n′)⟩=0,n′=0,
可知
∑
k
∈
Z
h
φ
(
k
)
h
φ
(
k
−
2
n
′
)
=
h
φ
⋆
h
φ
′
(
2
n
′
)
=
0
,
n
′
≠
0
h
φ
′
(
k
)
=
h
φ
(
−
k
)
.
\sum_{k \in \mathbb{Z}} h_{\varphi}(k)h_{\varphi}(k-2n') = h_{\varphi} \star h_{\varphi}' (2n') = 0, n' \not = 0\\ h_{\varphi}'(k) = h_{\varphi}(-k).
k∈Z∑hφ(k)hφ(k−2n′)=hφ⋆hφ′(2n′)=0,n′=0hφ′(k)=hφ(−k).
注: 这里 ⋆ \star ⋆为卷积符号.
这说明, { h φ } \{h_{\varphi}\} {hφ}偶数个是正交向量组. 其重要意义, 请看refer部分.
Wavelet Functions
既然
V
j
⊂
V
j
+
1
,
V_{j} \subset V_{j+1},
Vj⊂Vj+1,
那么, 我们可以进而定义正交补
W
j
W_j
Wj满足:
V
j
+
1
=
V
j
⊕
W
j
,
V_{j+1} = V_j \oplus W_j,
Vj+1=Vj⊕Wj,
且
⟨
f
,
g
⟩
=
0
,
∀
f
∈
V
j
,
g
∈
W
j
,
\langle f, g \rangle = 0, \quad \forall f \in V_j, g \in W_j,
⟨f,g⟩=0,∀f∈Vj,g∈Wj,
进一步, 我们可以知道
V
j
=
V
j
0
⊕
W
j
0
⊕
W
j
0
+
1
⊕
⋯
⊕
W
j
−
1
,
V_{j} = V_{j_0} \oplus W_{j_0} \oplus W_{j_0 + 1} \oplus \cdots \oplus W_{j-1},
Vj=Vj0⊕Wj0⊕Wj0+1⊕⋯⊕Wj−1,
且
⟨
f
,
g
⟩
=
0
,
∀
f
∈
V
i
,
∀
g
∈
W
j
,
i
≤
j
,
⟨
f
,
g
⟩
=
0
,
∀
f
∈
W
i
,
∀
g
∈
W
j
,
i
≠
j
.
\langle f, g \rangle = 0, \quad \forall f\in V_i, \forall g \in W_j, i \le j, \\ \langle f, g \rangle = 0, \quad \forall f\in W_i, \forall g \in W_j, i\not=j.
⟨f,g⟩=0,∀f∈Vi,∀g∈Wj,i≤j,⟨f,g⟩=0,∀f∈Wi,∀g∈Wj,i=j.
倘若
W
j
W_j
Wj由下列满足上述4个条件的函数:
ψ
j
,
k
(
x
)
=
2
j
/
2
ψ
(
2
j
x
−
k
)
,
\psi_{j, k}(x) = 2^{j/2} \psi (2^j x - k),
ψj,k(x)=2j/2ψ(2jx−k),
生成, 即
W
j
:
=
s
p
a
n
{
ψ
j
,
k
∣
k
∈
Z
}
‾
.
W_j := \overline{\mathrm{span}\{\psi_{j, k}| k \in \mathbb{Z}\}}.
Wj:=span{ψj,k∣k∈Z}.
同样有:
ψ
(
x
)
=
∑
k
∈
Z
h
ψ
(
k
)
2
φ
(
2
x
−
k
)
,
ψ
j
,
n
(
x
)
=
∑
k
∈
Z
h
φ
(
k
)
ψ
j
,
2
n
+
k
(
x
)
.
\psi (x) = \sum_{k \in \mathbb{Z}} h_{\psi}(k) \sqrt{2} \varphi (2x - k), \\ \psi_{j, n}(x) = \sum_{k \in \mathbb{Z}} h_{\varphi}(k)\psi_{j, 2n+k}(x).
ψ(x)=k∈Z∑hψ(k)2φ(2x−k),ψj,n(x)=k∈Z∑hφ(k)ψj,2n+k(x).
以及
∑
k
∈
Z
h
ψ
(
k
)
h
ψ
(
k
−
2
n
′
)
=
h
ψ
⋆
h
ψ
′
(
2
n
′
)
=
0
,
n
′
≠
0
h
ψ
′
(
k
)
=
h
ψ
(
−
k
)
.
\sum_{k \in \mathbb{Z}} h_{\psi}(k)h_{\psi}(k-2n') = h_{\psi} \star h_{\psi}' (2n') = 0, n' \not = 0\\ h_{\psi}'(k) = h_{\psi}(-k).
k∈Z∑hψ(k)hψ(k−2n′)=hψ⋆hψ′(2n′)=0,n′=0hψ′(k)=hψ(−k).
倘若我们通过
⟨
ψ
j
,
n
(
x
)
,
φ
j
,
n
(
x
−
k
)
⟩
=
0
,
\langle \psi_{j, n}(x), \varphi_{j, n}(x - k) \rangle = 0,
⟨ψj,n(x),φj,n(x−k)⟩=0,
可以得出
∑
k
∈
Z
h
ψ
(
k
)
h
φ
(
k
−
2
n
′
)
=
h
ψ
⋆
h
φ
′
(
2
n
′
)
=
0
,
n
′
≠
0.
\sum_{k \in \mathbb{Z}} h_{\psi}(k)h_{\varphi}(k-2n') = h_{\psi} \star h_{\varphi}' (2n') = 0, n' \not = 0.\\
k∈Z∑hψ(k)hφ(k−2n′)=hψ⋆hφ′(2n′)=0,n′=0.
这说明 h φ ( 2 n ) h_{\varphi}(2n) hφ(2n), 加上 h ψ ( 2 n ) h_{\psi}(2n) hψ(2n)能够构成正交基.
二者的联系
实际上, 可以证明(没去找这个证明),
h
ψ
(
k
)
=
(
−
1
)
k
h
φ
(
1
−
k
)
.
h_{\psi}(k) = (-1)^k h_{\varphi}(1-k).
hψ(k)=(−1)khφ(1−k).
以haar小波为例:
φ
(
x
)
=
{
1
0
≤
x
<
1
,
0
otherwise
.
\varphi(x) = \left \{ \begin{array}{ll} 1 & 0 \le x < 1, \\ 0 & \text{otherwise}. \end{array} \right .
φ(x)={100≤x<1,otherwise.
φ 0 , k ( x ) = 1 2 φ 1 , 2 k ( x ) + 1 2 φ 1 , 2 k + 1 ( x ) , \varphi_{0, k}(x) = \frac{1}{\sqrt{2}}\varphi_{1, 2k}(x) + \frac{1}{\sqrt{2}}\varphi_{1, 2k+1}(x), φ0,k(x)=21φ1,2k(x)+21φ1,2k+1(x),
所以
h
φ
(
0
)
=
h
φ
(
1
)
=
1
2
,
h
φ
(
n
)
=
0
,
n
≠
0
,
1.
h
ψ
(
0
)
=
1
2
,
h
ψ
(
1
)
=
−
1
2
,
h
ψ
(
n
)
=
0
,
n
≠
0
,
1.
h_{\varphi}(0) = h_{\varphi}(1) = \frac{1}{\sqrt{2}}, \\ h_{\varphi}(n) = 0, \quad n \not =0 ,1. \\ h_{\psi}(0) = \frac{1}{\sqrt{2}}, \\ h_{\psi}(1) = -\frac{1}{\sqrt{2}}, \\ h_{\psi}(n) = 0, \quad n \not =0 ,1.
hφ(0)=hφ(1)=21,hφ(n)=0,n=0,1.hψ(0)=21,hψ(1)=−21,hψ(n)=0,n=0,1.
离散的情形
上面的说明实际上都是在围绕平方可积的函数 φ \varphi φ说明的, 在离散的情况下需要特殊的处理(此处只能写点自己的理解了, 不是特别明白). 以haar小波为例:
φ
~
j
,
k
(
x
)
=
φ
j
,
k
(
x
N
)
,
x
=
0
,
1
,
⋯
,
N
−
1.
\tilde{\varphi}_{j, k}(x) = \varphi_{j, k}(\frac{x}{N}), \quad x = 0, 1, \cdots, N-1.
φ~j,k(x)=φj,k(Nx),x=0,1,⋯,N−1.
因为
φ
\varphi
φ的支撑是
[
0
,
1
]
[0, 1]
[0,1]. 以
N
=
4
N=4
N=4为例:
[
1
1
1
1
1
1
−
1
−
1
2
−
2
0
0
0
0
2
−
2
]
→
φ
0
,
0
→
φ
0
,
1
→
φ
1
,
0
→
φ
1
,
1
.
\left [ \begin{array}{cccc} 1 & 1 & 1 & 1 \\ 1 & 1 & -1 & -1 \\ \sqrt{2} & -\sqrt{2} & 0 & 0 \\ 0 & 0 & \sqrt{2} & -\sqrt{2} \end{array} \right ] \begin{array}{c} \rightarrow \varphi_{0, 0} \\ \rightarrow \varphi_{0, 1} \\ \rightarrow \varphi_{1, 0} \\ \rightarrow \varphi_{1, 1} \\ \end{array}.
⎣⎢⎢⎡112011−201−1021−10−2⎦⎥⎥⎤→φ0,0→φ0,1→φ1,0→φ1,1.
但是需要注意的是,
h
φ
h_{\varphi}
hφ是不变的(既然我们只是等式两边都需要进行相同的变量替换).
只是, 问题是, 如何证明离散后的向量之间依旧能够保持正交关系(应该是需要别的条件吧). 不过幸运的是 h h h之间的正交关系是保持的.
高效变换
假设我们已经求出
{
h
φ
,
h
ψ
}
\{h_{\varphi}, h_{\psi}\}
{hφ,hψ}, 如何快速计算系数:
c
,
d
,
T
.
c, d, T.
c,d,T.
实际上,
c
j
(
k
)
=
∑
n
h
φ
(
n
−
2
k
)
c
j
+
1
(
n
)
=
c
⋆
h
φ
′
(
2
k
)
,
d
j
(
k
)
=
∑
n
h
ψ
(
n
−
2
k
)
c
j
+
1
(
n
)
=
c
⋆
h
ψ
′
(
2
k
)
,
T
φ
(
j
,
k
)
=
∑
n
h
φ
(
n
−
2
k
)
T
φ
(
j
+
1
,
n
)
=
T
φ
(
j
+
1
,
⋅
)
⋆
h
φ
′
(
2
k
)
,
T
ψ
(
j
,
k
)
=
∑
n
h
ψ
(
n
−
2
k
)
T
φ
(
j
+
1
,
n
)
=
T
φ
(
j
+
1
,
⋅
)
⋆
h
ψ
′
(
2
k
)
.
c_j(k) = \sum_{n} h_{\varphi}(n - 2k) c_{j+1}(n) = c \star h_{\varphi}' (2k), \\ d_j(k) = \sum_{n} h_{\psi}(n - 2k) c_{j+1}(n) = c \star h_{\psi}'(2k), \\ T_{\varphi}(j, k) = \sum_{n} h_{\varphi}(n-2k)T_{\varphi}(j+1, n) = T_{\varphi}(j + 1, \cdot) \star h_{\varphi}' (2k), \\ T_{\psi}(j, k) = \sum_{n} h_{\psi}(n-2k)T_{\varphi}(j+1, n) = T_{\varphi}(j + 1, \cdot) \star h_{\psi}' (2k). \\
cj(k)=n∑hφ(n−2k)cj+1(n)=c⋆hφ′(2k),dj(k)=n∑hψ(n−2k)cj+1(n)=c⋆hψ′(2k),Tφ(j,k)=n∑hφ(n−2k)Tφ(j+1,n)=Tφ(j+1,⋅)⋆hφ′(2k),Tψ(j,k)=n∑hψ(n−2k)Tφ(j+1,n)=Tφ(j+1,⋅)⋆hψ′(2k).
从上面的公式可以看出, 我们可以从后向前地逐步计算系数. 又
[
f
⋆
g
(
0
)
,
f
⋆
g
(
2
)
⋯
f
⋆
g
(
2
n
)
⋯
]
=
[
f
⋆
g
(
0
)
,
f
⋆
g
(
1
)
⋯
f
⋆
g
(
n
)
⋯
]
2
↓
,
[f \star g (0), f \star g (2) \cdots f\star g (2n) \cdots] = [f \star g (0), f \star g (1) \cdots f\star g (n) \cdots]_{2\downarrow},
[f⋆g(0),f⋆g(2)⋯f⋆g(2n)⋯]=[f⋆g(0),f⋆g(1)⋯f⋆g(n)⋯]2↓,
其中
2
↓
2\downarrow
2↓表示下采样, 即
y
2
↓
(
n
)
=
y
(
2
n
)
.
y_{2\downarrow}(n) = y(2n).
y2↓(n)=y(2n).
具体的计算流程便如下图所示:
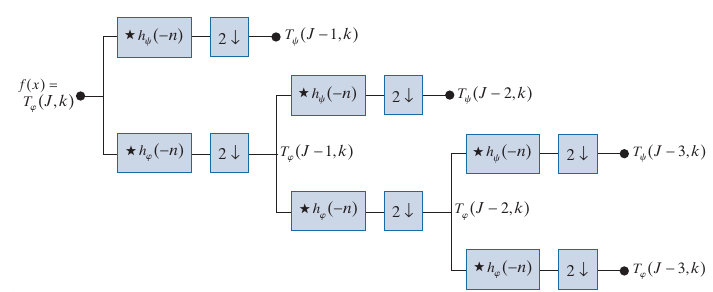
从上图可以看出, 我们首先需要知道 T φ ( J , k ) T_{\varphi}(J, k) Tφ(J,k), 但是实际上, 我们不会直接计算此, 而是直接从 f ( x ) f(x) f(x)中采样. 具体原因见p515 底部, 但是说实话此解释并不是很理解, 这给我的感觉像是脱离了原来的基 φ , ψ \varphi, \psi φ,ψ了. 而且书中给出的例子中, φ , ψ \varphi, \psi φ,ψ也似乎只有一个计算 h h h的功能, 这让我对最初的变换的目标产生困惑, 但是暂时还是先不深入了.
我们可以通过下列的操作, 从叶节点回推之前的结果.
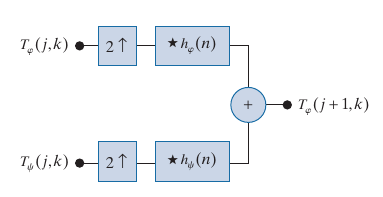
其原理如下:
注意到
h
⋆
f
(
n
)
=
∑
k
=
0
N
−
1
h
(
n
−
k
)
f
(
k
)
=
a
n
T
f
,
a
(
n
)
=
[
h
(
0
)
,
h
(
n
−
1
)
,
⋯
,
h
(
n
−
N
+
1
)
]
,
h \star f (n) = \sum_{k=0}^{N-1} h(n-k) f(k) = a^T_n f, \\ a(n) = [h(0), h(n-1), \cdots, h(n-N+1)],
h⋆f(n)=k=0∑N−1h(n−k)f(k)=anTf,a(n)=[h(0),h(n−1),⋯,h(n−N+1)],
则
A
=
[
a
0
,
a
1
,
⋯
,
a
N
−
1
]
=
[
h
(
0
)
h
(
1
)
⋯
h
(
N
−
1
)
h
(
−
1
)
h
(
0
)
⋯
h
(
N
−
2
)
⋮
⋮
⋱
⋮
h
(
1
−
N
)
h
(
2
−
N
)
⋯
h
(
0
)
,
]
[
h
⋆
f
]
=
A
T
f
.
A = [a_0, a_1, \cdots, a_{N-1}] = \left [ \begin{array}{cccc} h(0) & h(1) &\cdots & h(N-1) \\ h(-1) & h(0) & \cdots & h(N-2)\\ \vdots & \vdots & \ddots & \vdots \\ h(1-N) & h(2-N) & \cdots & h(0), \end{array} \right ] [h \star f] = A^T f.
A=[a0,a1,⋯,aN−1]=⎣⎢⎢⎢⎡h(0)h(−1)⋮h(1−N)h(1)h(0)⋮h(2−N)⋯⋯⋱⋯h(N−1)h(N−2)⋮h(0),⎦⎥⎥⎥⎤[h⋆f]=ATf.
定义
h
′
(
n
)
=
h
(
−
n
)
,
h'(n) = h(-n),
h′(n)=h(−n),
则有
[
h
′
⋆
f
]
=
A
f
.
[h' \star f] = Af.
[h′⋆f]=Af.
特别定义
A
φ
,
A
ψ
A_{\varphi}, A_{\psi}
Aφ,Aψ来特别指明
h
φ
,
h
ψ
h_{\varphi}, h_{\psi}
hφ,hψ所对于的矩阵,
A
φ
2
n
=
[
a
0
,
a
2
,
⋯
,
a
2
n
⋯
]
A_{\varphi_{2n}} = [a_0, a_2, \cdots, a_{2n} \cdots]
Aφ2n=[a0,a2,⋯,a2n⋯] 表示
A
φ
A_{\varphi}
Aφ的偶数行, 则
[
h
φ
′
⋆
f
]
2
↓
=
A
φ
2
n
f
,
[h_{\varphi}' \star f]_{2\downarrow} = {A_{\varphi_{2n}}} f,
[hφ′⋆f]2↓=Aφ2nf,
于是:
[
h
φ
⋆
[
h
φ
′
⋆
f
]
2
↓
2
↑
]
=
A
φ
2
n
T
A
φ
2
n
f
,
[h_{\varphi} \star [h_{\varphi}' \star f]_{2\downarrow 2 \uparrow}] = A_{\varphi_{2n}}^T{A_{\varphi_{2n}}} f,
[hφ⋆[hφ′⋆f]2↓2↑]=Aφ2nTAφ2nf,
类似地, 有
[
h
ψ
⋆
[
h
ψ
′
⋆
f
]
2
↓
2
↑
]
=
A
ψ
2
n
T
A
ψ
2
n
f
,
[h_{\psi} \star [h_{\psi}' \star f]_{2\downarrow 2 \uparrow}] = A_{\psi_{2n}}^T{A_{\psi_{2n}}} f,
[hψ⋆[hψ′⋆f]2↓2↑]=Aψ2nTAψ2nf,
又
A
φ
2
n
T
A
φ
2
n
+
A
ψ
2
n
T
A
ψ
2
n
=
[
A
φ
2
n
T
,
A
ψ
2
n
T
]
[
A
φ
2
n
A
ψ
2
n
]
=
I
,
A^T_{\varphi_{2n}} A_{\varphi_{2n}} +A^T_{\psi{2n}} A_{\psi{2n}}= [A_{\varphi_{2n}}^T, A_{\psi_{2n}}^T] \left [ \begin{array}{cc} A_{\varphi_{2n}}\\ A_{\psi_{2n}} \end{array} \right ] = I,
Aφ2nTAφ2n+Aψ2nTAψ2n=[Aφ2nT,Aψ2nT][Aφ2nAψ2n]=I,
这就保证了能够恢复
f
f
f, 这也是为什么需要
2
↓
,
2
↑
2\downarrow, 2\uparrow
2↓,2↑的原因.
注: 不论 j j j为多少, $ h \star f = \sum_{k=0}{2J-1}\dots$而不是 h ⋆ f = ∑ k = 0 2 j − 1 … h \star f = \sum_{k=0}^{2^j-1}\dots h⋆f=∑k=02j−1…, 个人感觉后者是推不出上面的结果的.
二维的情形
二维考虑可分的情况, 按照下面的基:
ϕ
(
x
,
y
)
=
φ
(
x
)
φ
(
y
)
,
ψ
H
(
x
,
y
)
=
ψ
(
x
)
φ
(
y
)
,
ψ
V
(
x
,
y
)
=
φ
(
x
)
ψ
(
y
)
,
ψ
D
(
x
,
y
)
=
ψ
(
x
)
ψ
(
y
)
.
\phi (x, y) = \varphi(x)\varphi(y), \\ \psi^H (x, y) = \psi(x)\varphi(y), \\ \psi^V (x, y) = \varphi(x)\psi(y), \\ \psi^D (x, y) = \psi(x)\psi(y). \\
ϕ(x,y)=φ(x)φ(y),ψH(x,y)=ψ(x)φ(y),ψV(x,y)=φ(x)ψ(y),ψD(x,y)=ψ(x)ψ(y).
容易证明上面能够构成一组基.
假设
f
(
x
,
y
)
,
x
=
0
,
1
,
⋯
,
2
J
1
−
1
,
y
=
0
,
1
,
⋯
,
2
J
2
−
1
.
f(x, y), \quad x = 0, 1, \cdots, 2^{J_1-1}, y = 0 ,1 ,\cdots, 2^{J_2-1}.
f(x,y),x=0,1,⋯,2J1−1,y=0,1,⋯,2J2−1.
为了计算对应的系数, 步骤如下:
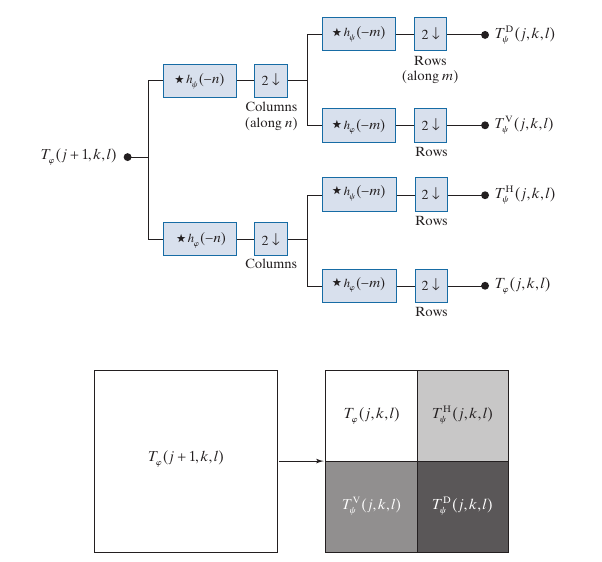
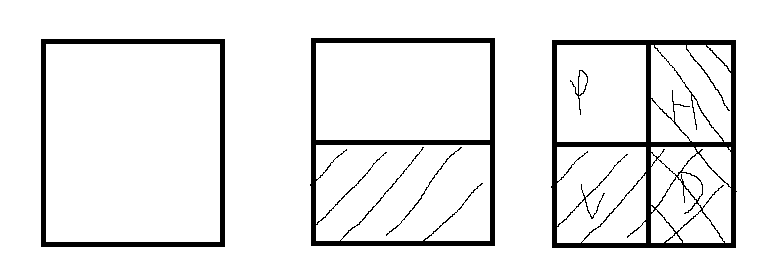
计算的过程, 实际上就是将逐步采用一维的方式来(既然基是可分的), 第一步, 沿着 x x x轴, 对每一列采取一维的DWT, 分别得到高频和低频信息, 如上图的阴影部分表示高频部分. 然后再在此基础上, 对于每一行采取一维的DWT, 再区分高频和低频信息. 故 ϕ \phi ϕ实际上提取的是低频信息, ψ H \psi^H ψH实际上提取的是水平方向的高频信息, ψ V \psi^V ψV提取的是垂直方向上的高频信息, ψ D \psi^D ψD是整体的高频信息(对角).
示例
import numpy as np
import matplotlib.pyplot as plt
import pywt
from PIL import Image
img = np.array(Image.open("Lenna.jpg").convert('L'))
LL, (LH, HL, HH) = pywt.dwt2(img, 'haar')
fig, axes = plt.subplots(2, 2)
axes[0, 0].imshow(LL, cmap=plt.cm.gray)
axes[0, 1].imshow(LH, cmap=plt.cm.gray)
axes[1, 0].imshow(HL, cmap=plt.cm.gray)
axes[1, 1].imshow(HH, cmap=plt.cm.gray)
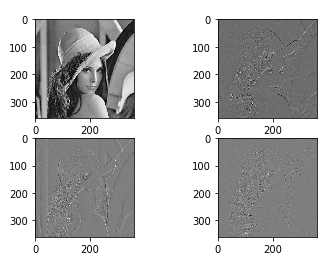








 本文深入探讨了小波变换的理论基础,包括Scaling Functions和Wavelet Functions的定义及其相互关系。通过离散情形的分析,展示了如何实现高效的变换计算。此外,还介绍了二维小波变换的应用,并给出了一个实际的图像处理示例,展示如何使用PyWavelets库进行二维离散小波变换。
本文深入探讨了小波变换的理论基础,包括Scaling Functions和Wavelet Functions的定义及其相互关系。通过离散情形的分析,展示了如何实现高效的变换计算。此外,还介绍了二维小波变换的应用,并给出了一个实际的图像处理示例,展示如何使用PyWavelets库进行二维离散小波变换。
















 4043
4043

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








