_数据结构_堆_堆排序

堆的概念

如果有一个关键码的集合K = {k0，k1， k2，…，kn-1}，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足：Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0，1，2…，则称为小堆(或大堆)。
将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

堆 一定是一棵 完全二叉树

当根结点为 i 时：
其左子结点为：2i+1； 右子结点为2i+2

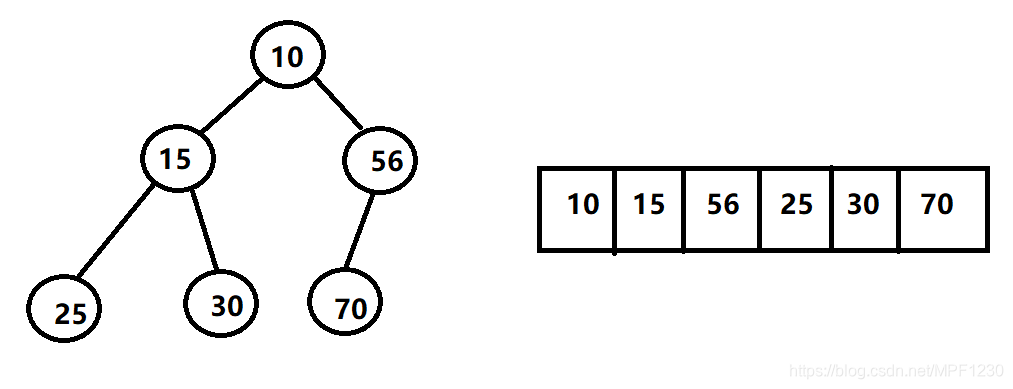
堆的存储顺序 就是 二叉树层序遍历的顺序

堆的创建

拿大根堆来说，因为堆的定义，每一棵子树的根结点，一定比两个子结点的的值要大，所以每插入一个结点时，都需要调整整个二叉树的结构，保证每个子树的根结点大于其子结点。

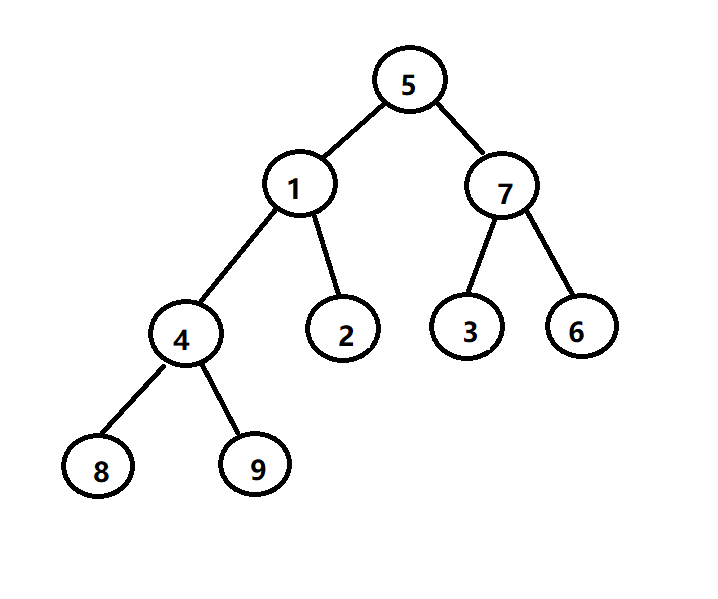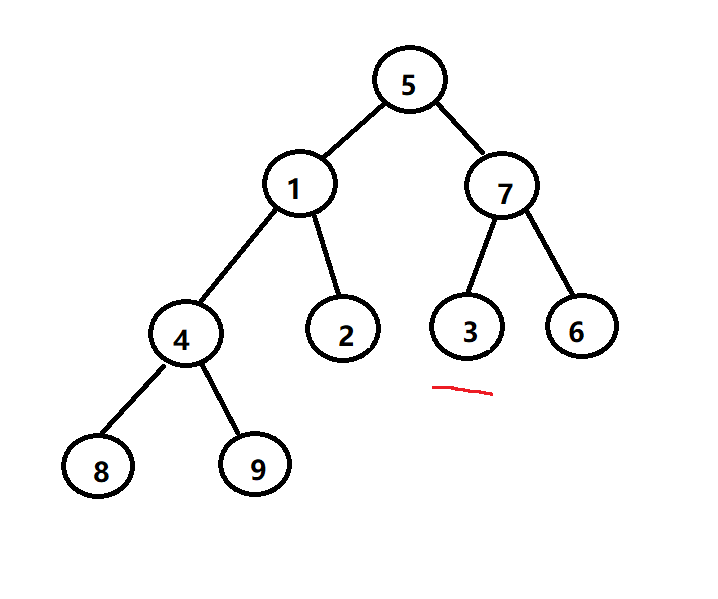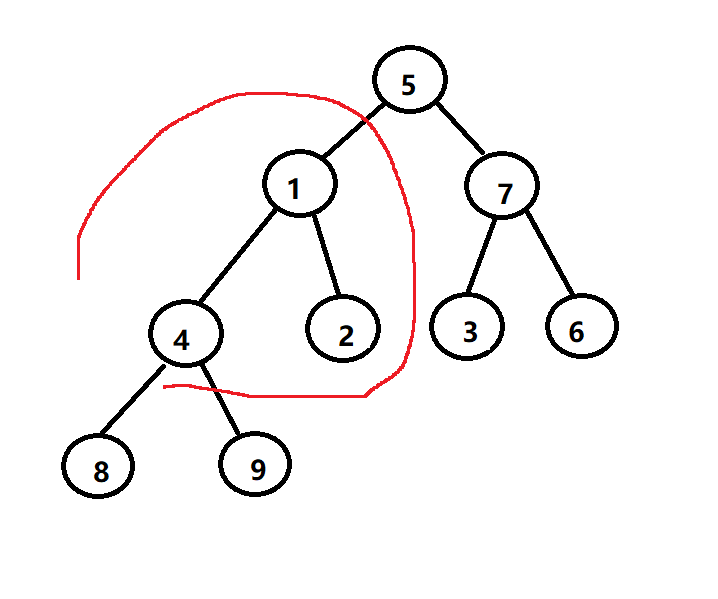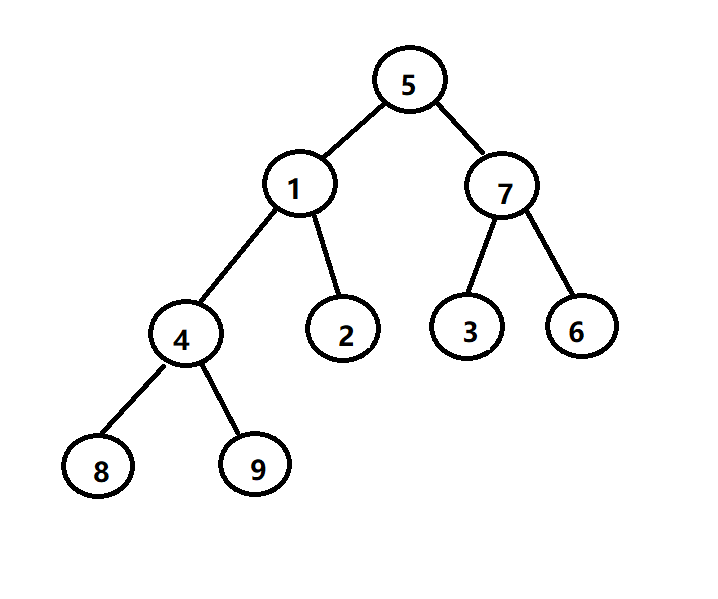
向上调整算法

像上调整算法也就是从底向上，从第一个非叶子结点开始，对比其根与孩子结点的大小，如果比其中孩子的值小，则调整两者位置，继续向上找上一个子树的根结点，直到调整到最上层。

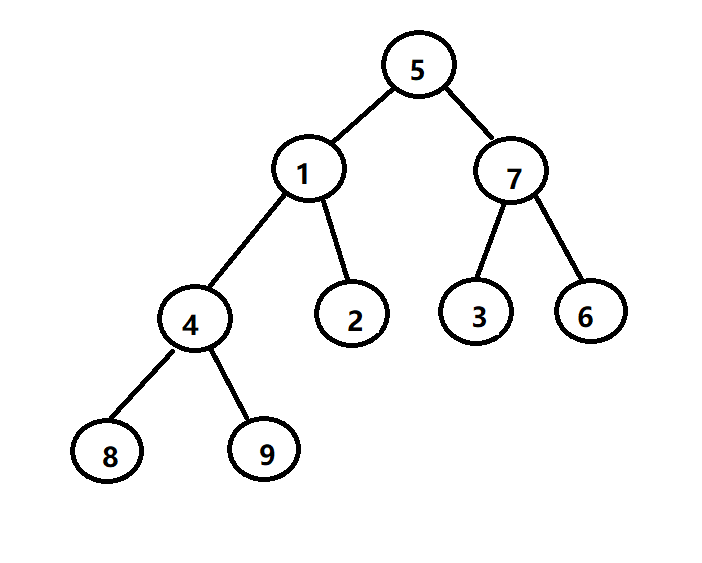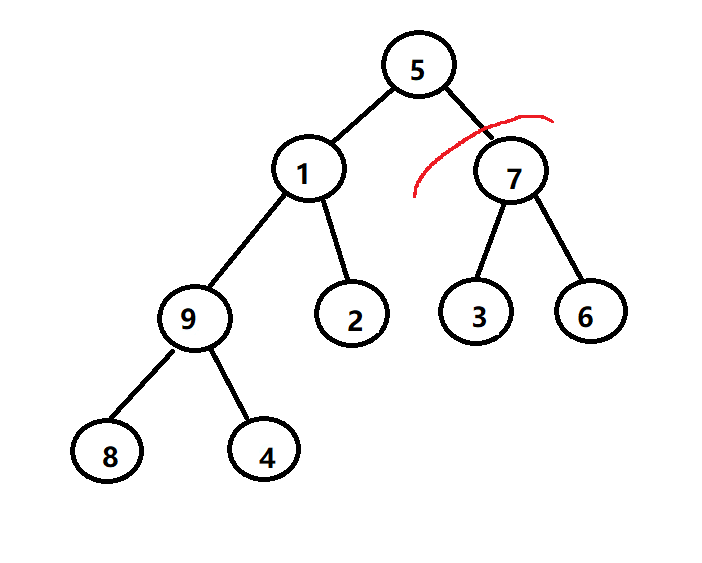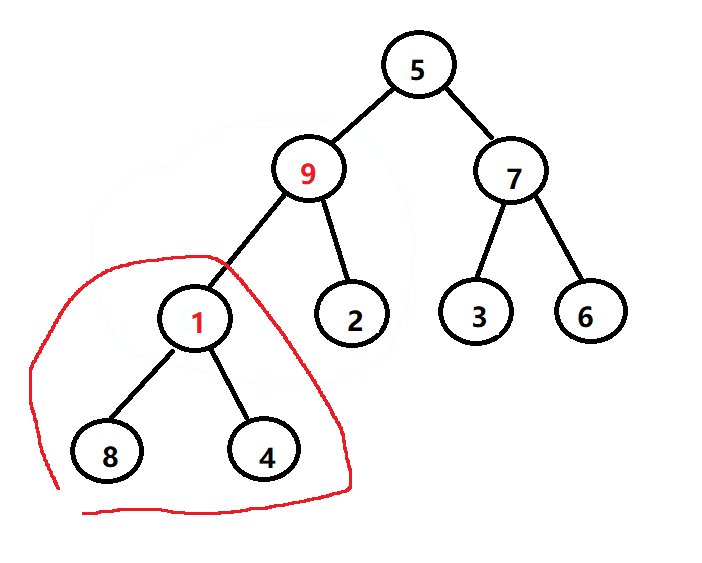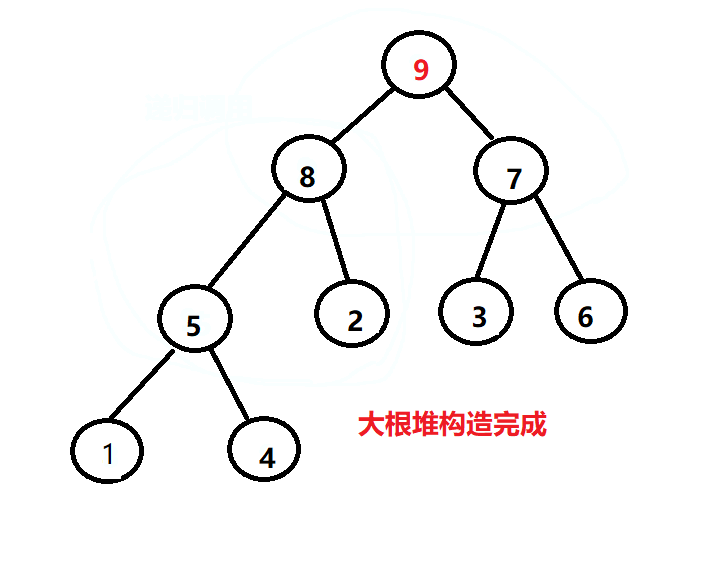
每当在向上调整时，有两个结点发生位置调换时，则将调换过的叶子结点位置，作为根结点进行递归操作，保证调换后，不会打乱其他堆的平衡。

调整算法

void swap(int* heap, int i, int j)
{
	int temp = heap[i];
	heap[i] = heap[j];
	heap[j] = temp;
}

void heapify(int* heap,int n,int i)
{
	int max = i;
	int cl = 2 * i + 1; //左子结点
	int cr = 2 * i + 2; //右子结点
	if (i >= n)
	{
		return;
	}
	if (cl<n&&heap[cl]>heap[max])  
	{
		max = cl;
	}
	if (cr<n&&heap[cr]>heap[max])
	{
		max = cr;
	}
	if (max != i)
	{
		swap(heap, max, i);
		heapify(heap, n, max);
	}
}

通过向上调整算法构造堆

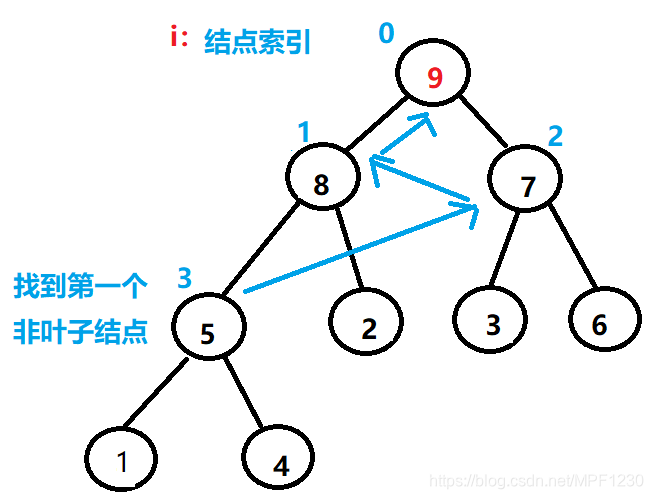
构造堆，需要先找到第一个非叶子结点，也就是数组下标为4的位置，依次递减，就可以遍历所有子树，调整根与子结点的位置。

问题是如何找到第一个非叶子结点。

堆的总量为 n ，因为下标是从0开始的，所以用n-2的范围，一定是最后两个叶子结点的范围，所以(n-2)/2，便能找到这两个叶子结点的根结点。

void build_heap(int* heap, int n)
{
	int parent = (n - 2) / 2;
	for (int i = parent; i >= 0; i--)
	{
		heapify(heap, n, i);
	}
}

堆排序

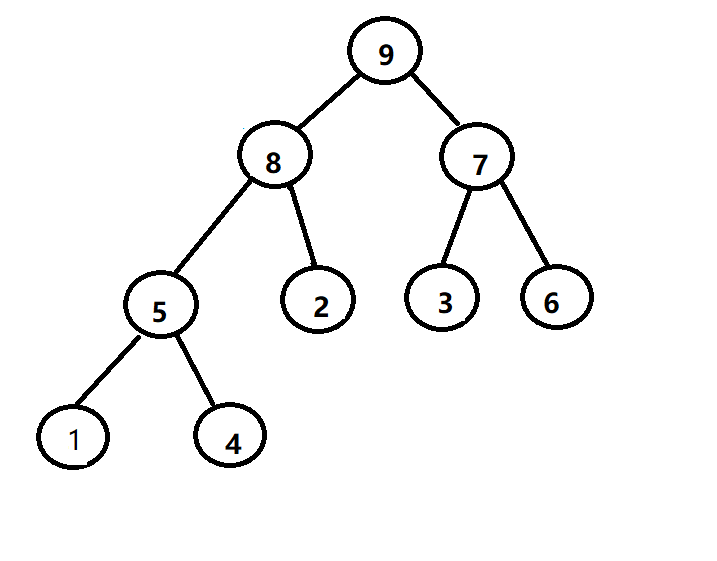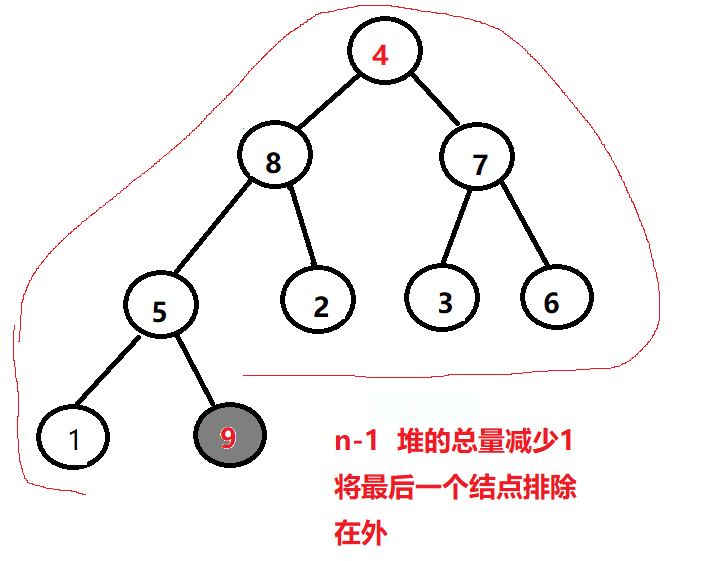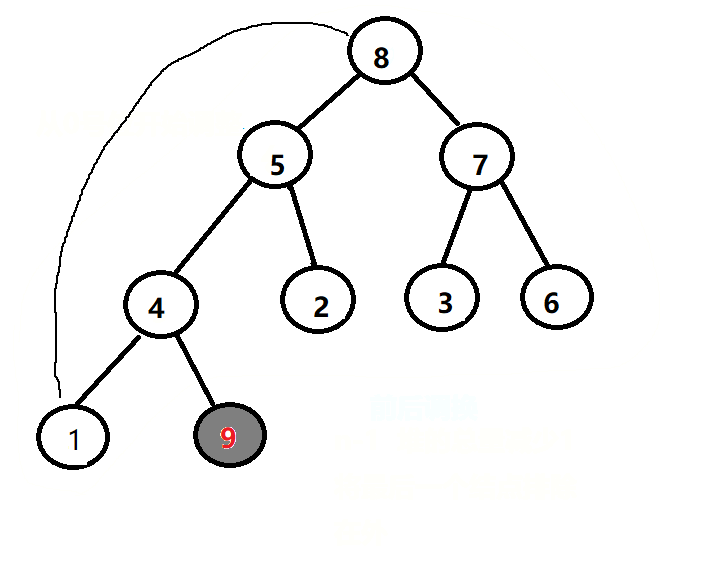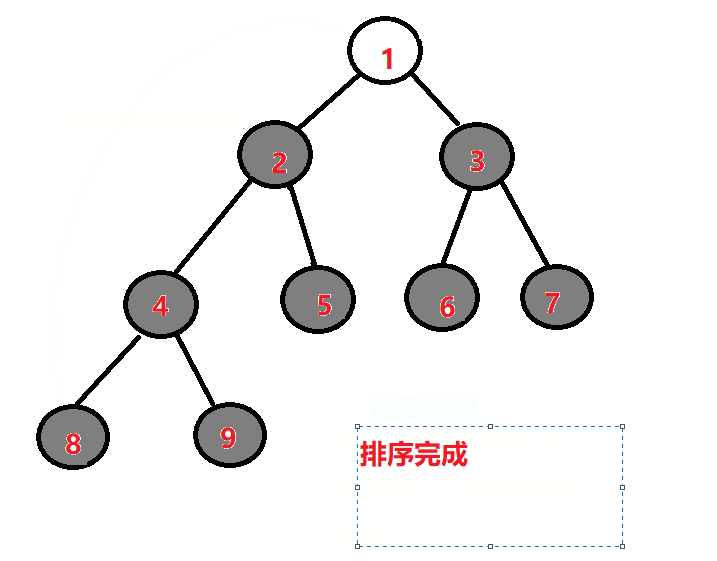
应为大根堆的特性，根结点一定大于其子结点，所以 0 号位的结点，一定是整个堆中最大的元素，所以每次我们将根结点与当前最后一个结点交换位置，将堆总量n-1，把最后一个元素排除在外，做向上调整。直到调整到最高位，最终就能得到升序的数组。

堆排代码

void heap_sort(int* heap, int n)
{
	build_heap(heap, 10);
	for (int i = n-1; i >= 0; i--)
	{
		swap(heap, 0, i);
		heapify(heap, i,0);
	}
}