判断一个点是否在三角形内部

判断一个点是否在三角形内部

题目描述

在二维坐标系中，所有的值都是double类型，那么一个三角形可以由3个点来代表，给定3个点代表的三角形，再给定一个点(x, y)，判断(x, y)是否在三角形中

输入描述：

输入有四行，每行两个浮点数。

前三行的6个数分别代表三角形的三个顶点的坐标

最后两个数分别表示(x, y)

输出描述：

若(x, y)在三角形中，输出"Yes"，否则输出"No"

示例1

输入

-1.00 0.00
1.50 3.50
2.73 -3.12
1.23 0.23

输出

Yes

说明

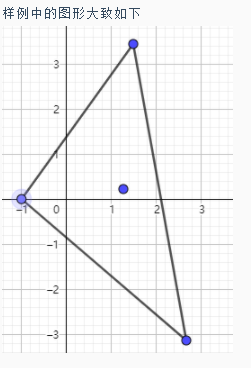
示例2

输入

-1.00 0.00
1.50 3.50
2.73 -3.12
2333.33 233333.33

输出

No

备注：

$-2\ast 10^{10}⩽x_i,y_i,x,y⩽2\ast 10^{10}$

---

题解：

与 判断一个点是否在矩形内部 解法一致，并且这题可以循环进行判断，不至于一个个枚举判断。但是，此题的输入顺序不知道，可能乱序，需要处理一下乱序的情况。

代码：

#include <cstdio>
#include <algorithm>

using namespace std;

double x[4], y[4];

inline double cross_product( int i, int j, int k ) {
    return (x[k] - x[i]) * (y[j] - y[i]) - (x[j] - x[i]) * (y[k] - y[i]);
}

int main(void) {
    for ( int i = 0; i < 4; ++i )
        scanf("%lf%lf", x + i, y + i);
    if ( cross_product( 0, 2, 1 ) > 0 ) {
        swap( x[1], x[2] );
        swap( y[1], y[2] );
    }
    for ( int i = 0; i < 3; ++i ) {
        if ( cross_product(i, (i + 1) % 3, 3) < 0 ) return 0 * puts("No");
    }
    return 0 * puts("Yes");
}