二维数组典型应用题--矩阵最大平台

这次我们来讲讲一道二维数组典型应用题~

什么是二维数组呢？

定义类型：类型名 数组名[ 行表达式 ][ 列表达式]；行与列用常量表达式。

例如：a[100][100]这就开了一个一百乘一百的方阵数组(当然二维数组也可以开成长方形的)

 注：一个二维数组，在本质上是有多个一维数组构成。（每一个一维数的大小必须相同）

 例如：定义 int a[ 3 ][ 4 ] 的二维数组，它是由 3 个一维数组组成，每个一维数组的大小是 4 个整型元素。可以只对部分元素赋值，未赋值的元素自动取 0 值。

现在相信大家对二维数组都有一定的了解了吧！那我们来看看题目

下面是一个4*4的矩阵，它的特点是：(1)矩阵的元素都是正整数；(2)数值相等的元素相邻，这样，这个矩阵就形成了一级级“平台”，其上最大的“平台”面积为8，高度（元素值）为6。如果平台面积相等，那么高度大的为最大“平台”。

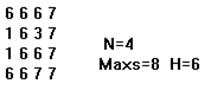
若有一个已知的n*n的矩阵也具有上面矩阵的特点，求矩阵最大“平台”的面积和高度。

输入格式

第一行一正整数n（小于等于100）；

接下来n行为n*n矩阵，其中每行有n个用单个空格隔开的小于等于100000的非负整数。

输出格式

矩阵最大“平台”的面积和高度。

输入/输出例子1

输入：

4

6 6 6 7

1 6 3 7

1 6 6 7

6 6 7 7 

输出：

8 6

相信大佬们很快就能理解并看懂，那么我就直接上代码了

#include<bits/stdc++.h>
using namespace std;
int a[105][105],n,x,y,m,ms,s,h;
int main(){
    cin>>n;
    for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) cin>>a[i][j];//输入，不解释了
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            if(a[i][j]>0)
            {
                s=0,m=a[i][j];
                for(x=i;x<=n;x++)
                {
                    for(y=j;y<=n;++y)
                        if(a[x][y]==m) a[x][y]=0,s++;
                }
                if(s>ms) ms=s,h=m;
                if(s==ms&&m>h) h=m;
            }
        }
    }
    cout<<ms<<" "<<h<<endl;
    return 0;
}