Week 10: 深度学习补遗：生成式模型

Week 10: 深度学习补遗：生成式模型

摘要

本周继续跟随李宏毅老师的课程进行学习，主要学习了VAE的数学表示以及生成对抗网络的设计概念，对生成式模型有了更深入的了解。

Abstract

This week, we continue to follow Mr. Hung-yi Lee’s course, focusing on the mathematical representation of VAE and the design concepts of generative adversarial networks to gain a deeper understanding of generative models.

1. VAE的数学解释

在VAE中，Code不再直接等于Encoder输出，因此，不仅需要最小化Input和Output之间的差距，同时还需要最小化${\sum }_{i=1}^3(exp({\sigma }_i)-(1+{\sigma }_i)+(m_i{)}^2)$。同时因为VAE训练过程中增加了噪声，因此会有更好的泛化效果，即可以通过控制Code对从未见过的中间状态进行更好的生成。而上式中，$m_i$为原编码，$exp({\sigma }_i)$为噪声，${\sigma }_i$则为噪声的方差，在学习中不断改变。而在重建损失中的$(m_i{)}^2$一项则相当于L2正则化，避免过拟合。

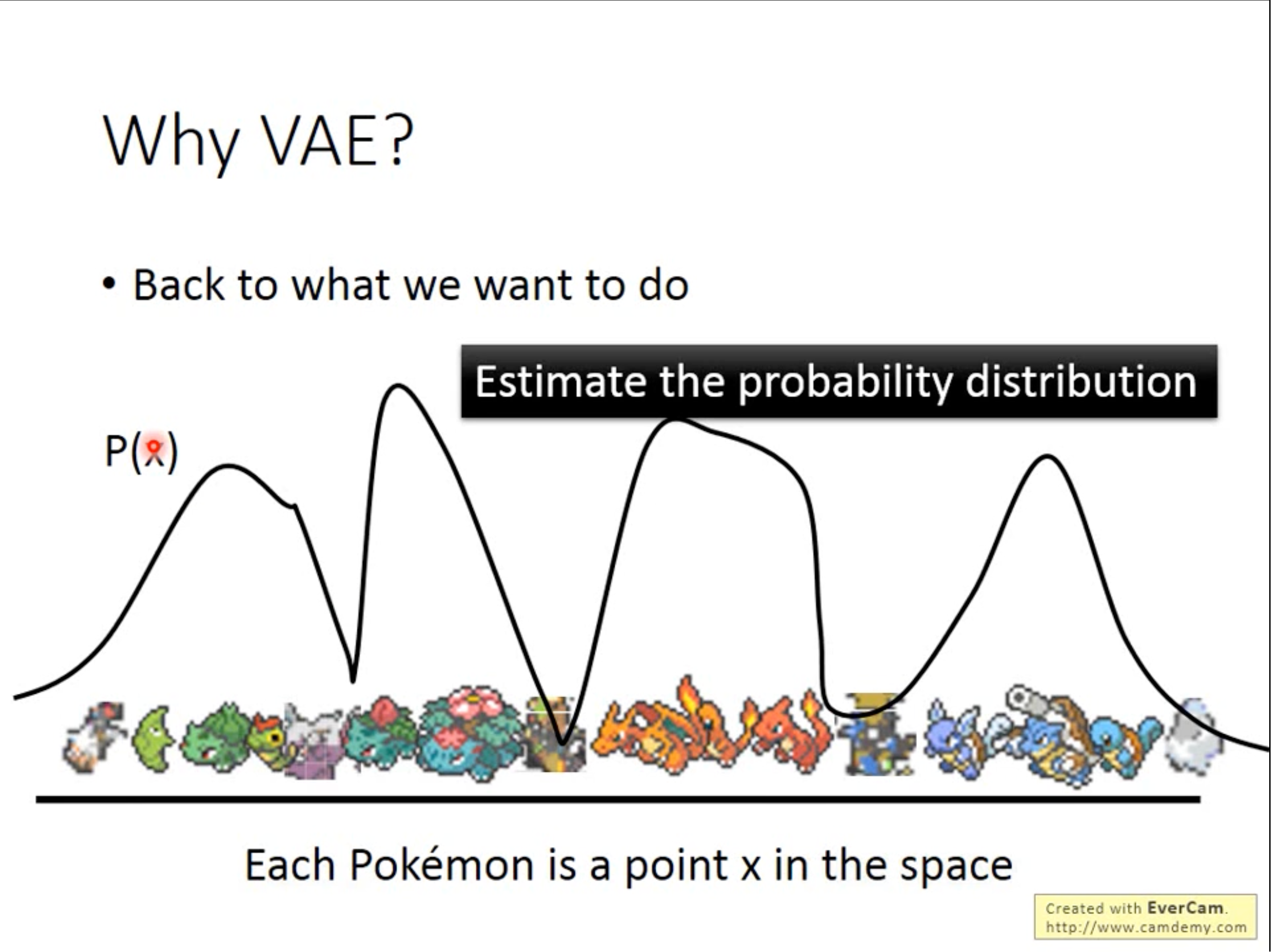
另一个角度来说，可以将每张图片认为是高维空间上的一点，VAE做的是正确的估计其概率分布。可以把点$x$看作是从某个分布中来的数据，而点$x$是一个向量，用其表示其属于各个分布的权重。VAE就是高斯混合模型的分布表示版本。
$$\begin{array}{rl}z& \sim N(0,I)\\ x|z& \sim N(\mu (z),\sigma (z))\\ P(x)& ={\int }_{z}P(z)P(x|z)dz\\ L& =\sum _x\log P(x)\end{array}$$
在$z$上采样到的点，会对应到一个高斯分布，由函数（可以是神经网络）决定其对应到哪一个高斯分布。还需要另一个分布$q(z|x)$来表示编码器，而$z|x\sim N({\mu }^{\prime }(z),{\sigma }^{\prime }(z))$。
$$\begin{array}{rl}\log P(x)& ={\int }_{z}q(z|x)\log P(x)dz\\ & ={\int }_{z}q(z|x)\log (\frac{P(z,x)}{P(z|x)})dz\\ & ={\int }_{z}q(z|x)\log (\frac{P(z,x)q(z|x)}{q(z|x)P(z|x)})dz\\ & ={\int }_{z}q(z|x)\log (\frac{P(z,x)}{q(z|x)})dz+\underset{KL(q(z|x)||P(z|x))\ge 0}{\underline{{\int }_{z}q(z|x)\log (\frac{q(z|x)}{P(z|x)})dz}}\\ & \ge {\int }_{z}q(z|x)\log (\frac{P(x|z)P(z)}{q(z|x)})dz\text{(下界}{L}_b\text{)}\\ \therefore L_b& ={\int }_{z}q(z|x)\log (\frac{P(x|z)P(z)}{q(z|x)})dz\end{array}$$
需要找到$P(x|z)$和$q(z|x)$，能最大化$L_b$。又因为$\log P(x)$只由KL散度和$L_b$决定，因此，让$q(z|x)$变大，可以使$L_b$变大，同时使KL散度最小。同时，让$P(x)$变大，就可以让目标$P(x)$最大化。
$$\begin{gathered} \text{Minimizing}KL(q(z|x)||P(z)) \\ \text{Maximizing}{\int }_{z}q(z|x)\log (P(x|z)dz)=E_{q(z|x)}[log(P(x|z))] \end{gathered}$$
但VAE最大的问题是，其并没有真正在学习产生一个图片的方法，而是只是在学习分布并对其进行模仿。

2. Generative Adversarial Networks 生成对抗网络

对比VAE来说，GAN具有拟态能力，分为生成器 Generator 和判别器 Discriminator 两个部分，通过生成器生成图片，让判别器分辨是否符合目标，再进行纠正。需要注意的是，生成器从未见过真正的图片。

• 首先，用各类别的带标注图片数据对判别器进行训练，使其对图片具有分辨能力。
• 将连接上生成器和判别器的大网络视为一整个网络。
• 固定住判别器的参数，对生成器进行训练，进行梯度下降优化生成器参数。

但是，实际上，GAN的训练并不简单。GAN非常难以优化，且没有一个很明确的指标可以衡量生成器（在普通的神经网络中，我们观测loss，但是在GAN中，必须观测生成器和判别器是否匹配良好）。而且，当判别器完全无法分辨出生成器生成的图片时，并不代表生成器非常厉害，很有可能是因为判别器太弱或者生成器找到了一个可以骗过判别器的特例。

总结

本周着重对两种生成式模型进行了学习，研究了VAE的数学原理和抽象模型原理以及生成对抗网络的设计思路，结合前几周所着重学习的无监督学习的知识以及词嵌入知识，对生成式模型的运作原理和几种经典的设计思路有了更加深入和全面的理解。