Week 5: 深度学习补遗：逻辑回归

Week 5: 深度学习补遗：逻辑回归

摘要

本周继续跟随李宏毅老师的课程学习，主要对逻辑回归相关内容进行了学习和推导，对多分类任务进行了更加深入的探索。同时，针对判别型模型与生成型模型的区别进行了数学上的推导，建立了一定的认识。

Abstract

This week, I continued to follow Professor Li Hongyi’s course learning, mainly studying and deriving content related to logistic regression, and exploring multi classification tasks in more depth. At the same time, mathematical deductions were made regarding the differences between discriminative models and generative models, establishing a certain understanding.

1. 逻辑回归的函数变化

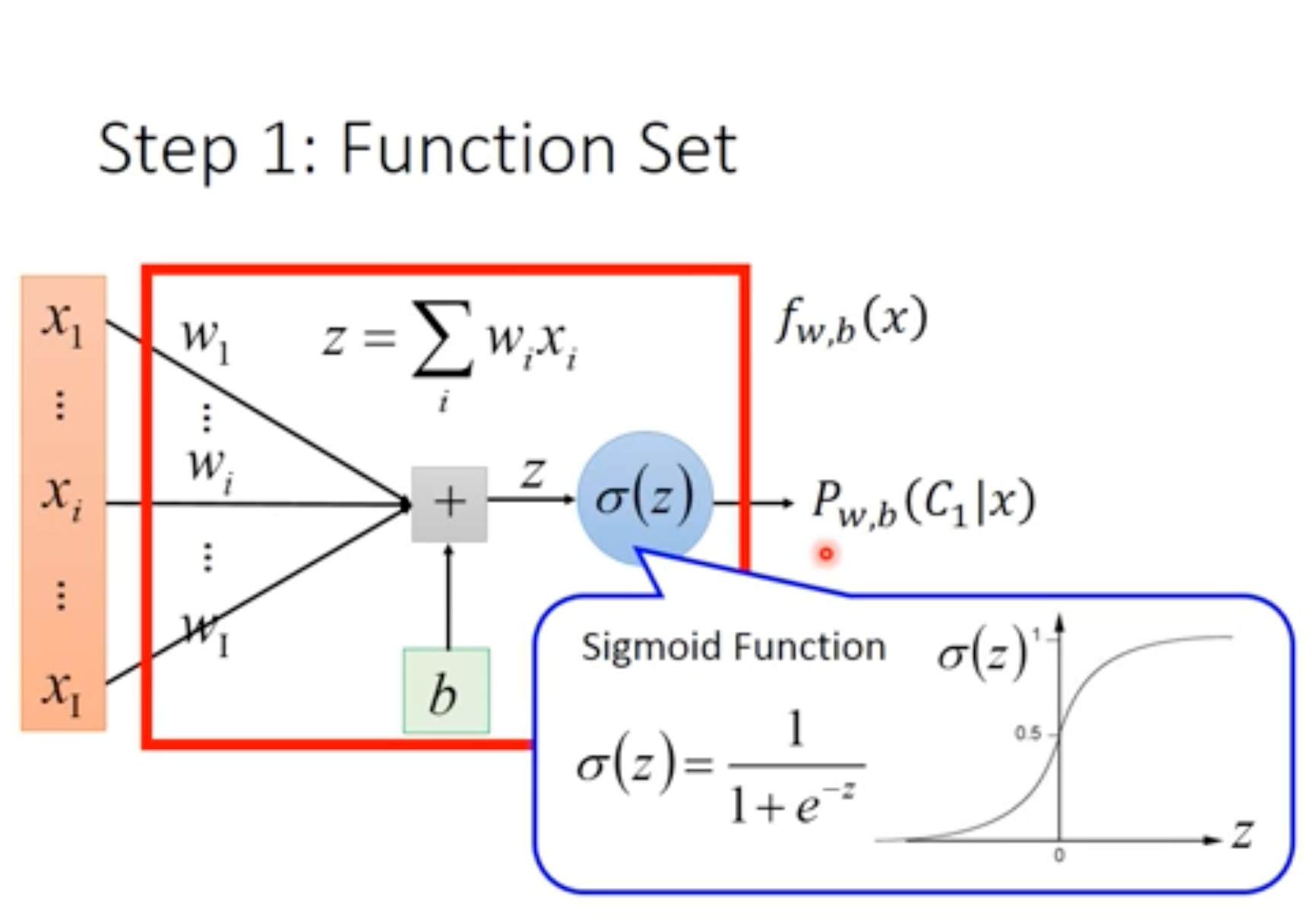
逻辑回归在线性回归的基础上加入了$Sigmoid$函数，使输出介于$(0,1)$之间，适用于分类问题，将线性输出结果转换为属于某个类别的概率。

图片来源：ML Lecture 5: Logistic Regression

2. 逻辑回归的损失变化

在上一章Week 4[Github / 优快云]中，提到利用似然函数$L(w,b)$衡量模型拟合程度的好坏。
$$\begin{array}{rl}L(w,b)& =f_{w,b}(x^1)f_{w,b}(x^2)(1-f_{w,b}(x^3))\dots f_{w,b}(x^N)\\ -\ln L(w,b)& =\ln f_{w,b}(x^1)+\ln f_{w,b}(x^2)+\ln (1-f_{w,b}(x^3))\cdots +\ln f_{w,b}(x^N)\\ & =\sum _n\underset{\text{Cross Entropy between two Bernoulli distribution}}{\underline{-[\hat{y}\ln f_{w,b}(x^n)+(1-\hat{y})\ln (1-f_{w,b}(x^n))]}}\end{array}$$

经过这样的变换，可以推出两个伯努利分布之间的交叉熵。而更加一般的两个分布之间的交叉熵可以表示为：
$$H(p,q)=-\sum _{x}p(x)\ln (q(x))$$
交叉熵代表着两个分布的接近程度，两个分布越接近，其交叉熵应越接近0。因此损失函数可以表示为：
$$\begin{array}{rl}L(f)& =\sum _{n}C(f(x^n),{\hat{y}}^n)\\ C(f(x^n),{\hat{y}}^n)& =-[{\hat{y}}^n\ln f(x^n)+(1-{\hat{y}}^n)\ln (1-\ln f(x^n))]\end{array}$$
求出模型分布与原分布的交叉熵，即模型预测分布于原分布的相似程度。

3. 逻辑回归损失函数的梯度下降法数学演算

对两个伯努利分布的交叉熵，即二分类问题的损失函数对需要进行梯度下降的参数求偏导。
∂ ( − ln ⁡ L ( w , b ) ) ∂ w i = ∑ n − [ y ^ ∂ ln ⁡ f w , b ( x n ) ∂ w i + ( 1 − y ^ ) ∂ ln ⁡ ( 1 − f w , b ( x n ) ) ∂ w i ] ∂ ln ⁡ f w , b ( x n ) ∂ w i = ∂ ln ⁡ f w , b ( x ) ∂ z ⋅ ∂ z ∂ w i ∂ z ∂ w i = x i ∵ f w , b ( x ) = σ ( z ) ∴ ∂ ln ⁡ f w , b ( x ) ∂ z = ∂ ln ⁡ σ ( z ) ∂ z = 1 σ ( z ) ⋅ σ ′ ( z ) = 1 − σ ( z ) ∂ ln ⁡ ( 1 − f w , b ( x n ) ) ∂ w i = ∂ ln ⁡ ( 1 − f w , b ( x n ) ) ∂ z ∂ z ∂ w i = ∂ ln ⁡ ( 1 − σ ( z ) ) ∂ z ⋅ x i = 1 1 − σ ( z ) ⋅ σ ′ ( z ) = σ ( z ) ⋅ x i 因此， ∂ ( − ln ⁡ L ( w , b ) ) ∂ w i = ∑