Least Square 最小二乘

最新推荐文章于 2022-02-26 11:44:12 发布

原创最新推荐文章于 2022-02-26 11:44:12 发布 · 567 阅读

1 ·

CC 4.0 BY-SA版权

博客介绍了最小平方直线和最小平方曲线的相关内容。对于最小平方直线，给出直线方程和平方误差公式，通过样本数据计算得出满足平方误差最小时的参数 k 和 b。当样本数据复杂时，引入最小平方曲线，给出通式并说明求解方法。

文章目录

- 最小平方直线 Least Square Line
- 最小平方曲线 Least Square Curve

最小平方直线 Least Square Line

直线方程：
$kx+b\tag{0}$
平方误差 $E$ 为：
$\sum_{i=1}^{n}(f(x_{i}) - y_{i}) \tag{1}$
其中， $k$ 和 $b$ 为待求参数， $x_{i}, y{i})$ 为已知样本。
已知 $n$ 个样本，则：

若n点已经共线，则此时 $f(x_{i}) = y_{i}$ ，即， $E = 0$ ，易得直线方程。
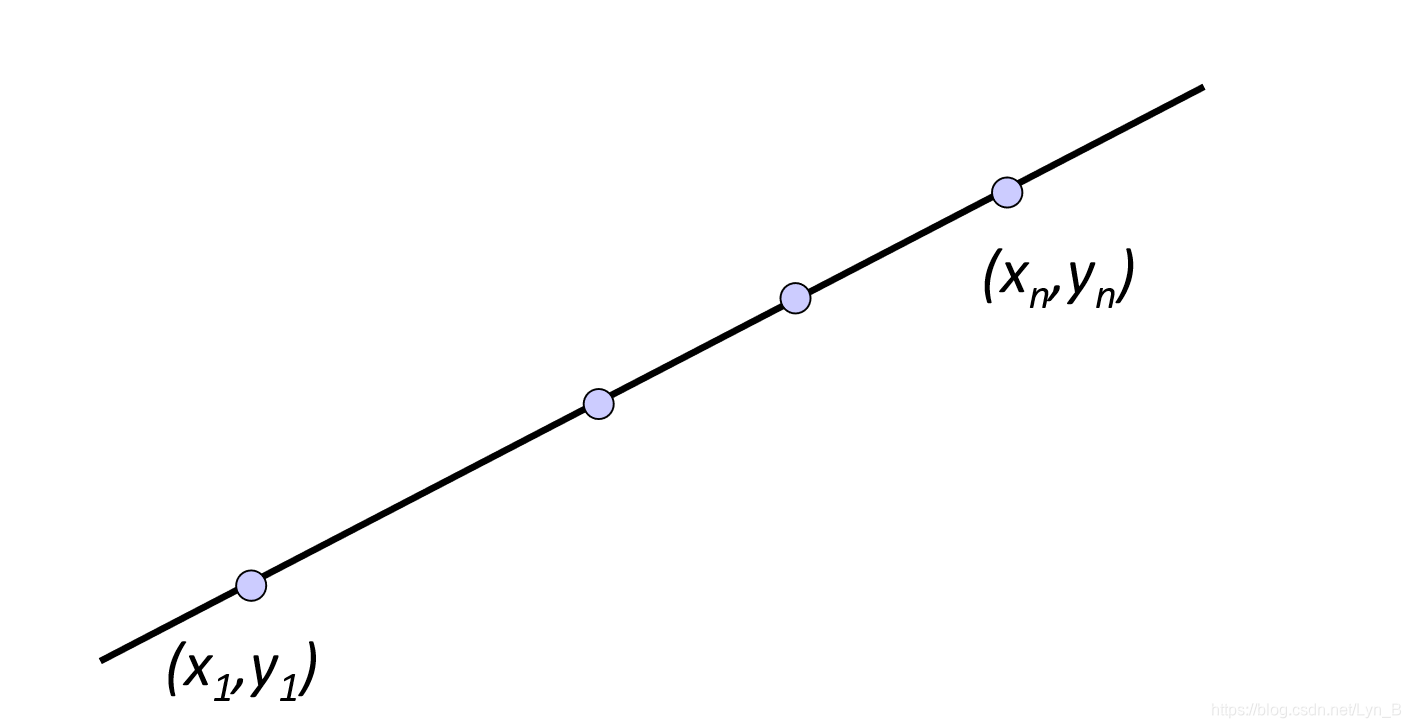
若样本为随机样本，如下：

则根据所设直线方程有：
$\begin{cases} kx_{1} + b = y_{1} \\ kx_{2} + b = y_{2} \\ kx_{3} + b = y_{3} \\ \dots \\ kx_{n} + b = y_{n} \end{cases} \tag{2}$
即：
$\left[ \begin{matrix} x_{1} & 1 \\ x_{2} & 1 \\ \dots &1 \\ x_{n} & 1 \end{matrix} \right] \left[ \begin{matrix} k \\ b \end{matrix} \right] = \left[ \begin{matrix} y_{1} \\ y_{2} \\ \dots \\ y_{n} \end{matrix} \right] \tag{3}$
左右同乘以左边包含 $x_{n}$ 矩阵的转置：
$\left[ \begin{matrix} x_{1} & x_{2} & \dots & x_{n} \\ 1 &1 & 1 & 1 \end{matrix} \right] \left[ \begin{matrix} x_{1} & 1 \\ x_{2} & 1 \\ \dots &1 \\ x_{n} & 1 \end{matrix} \right] \left[ \begin{matrix} k \\ b \end{matrix} \right] = \left[ \begin{matrix} x_{1} & x_{2} & \dots & x_{n} \\ 1 &1 & 1 & 1 \end{matrix} \right] \left[ \begin{matrix} y_{1} \\ y_{2} \\ \dots \\ y_{n} \end{matrix} \right] \tag{3}$
计算两个 $\times n$ 和 $\times n$ 的结果得到：
$\left[ \begin{matrix} \sum_{i=1}^{n}x_{i}^{2} & \sum_{i=1}^{n}x_{i}\\ \sum_{i=1}^{n}x_{i} & n \end{matrix} \begin{matrix} \end{matrix} \right] \left[ \begin{matrix} k \\ b \end{matrix} \right] = \left[ \begin{matrix} \sum_{i=1}^{n}x_{i}y_{i} \\ \sum_{i=1}^{n}y_{i} \end{matrix} \right] \tag{4}$
此时，当满足平方误差最小时，上面计算出的 $k$ 和 $b$ 将得到我们的最小二乘直线，即：
$\min E = \sum_{i=1}^{n}(f(x_{i}) - y_{i}) \tag{5}$

最小平方曲线 Least Square Curve

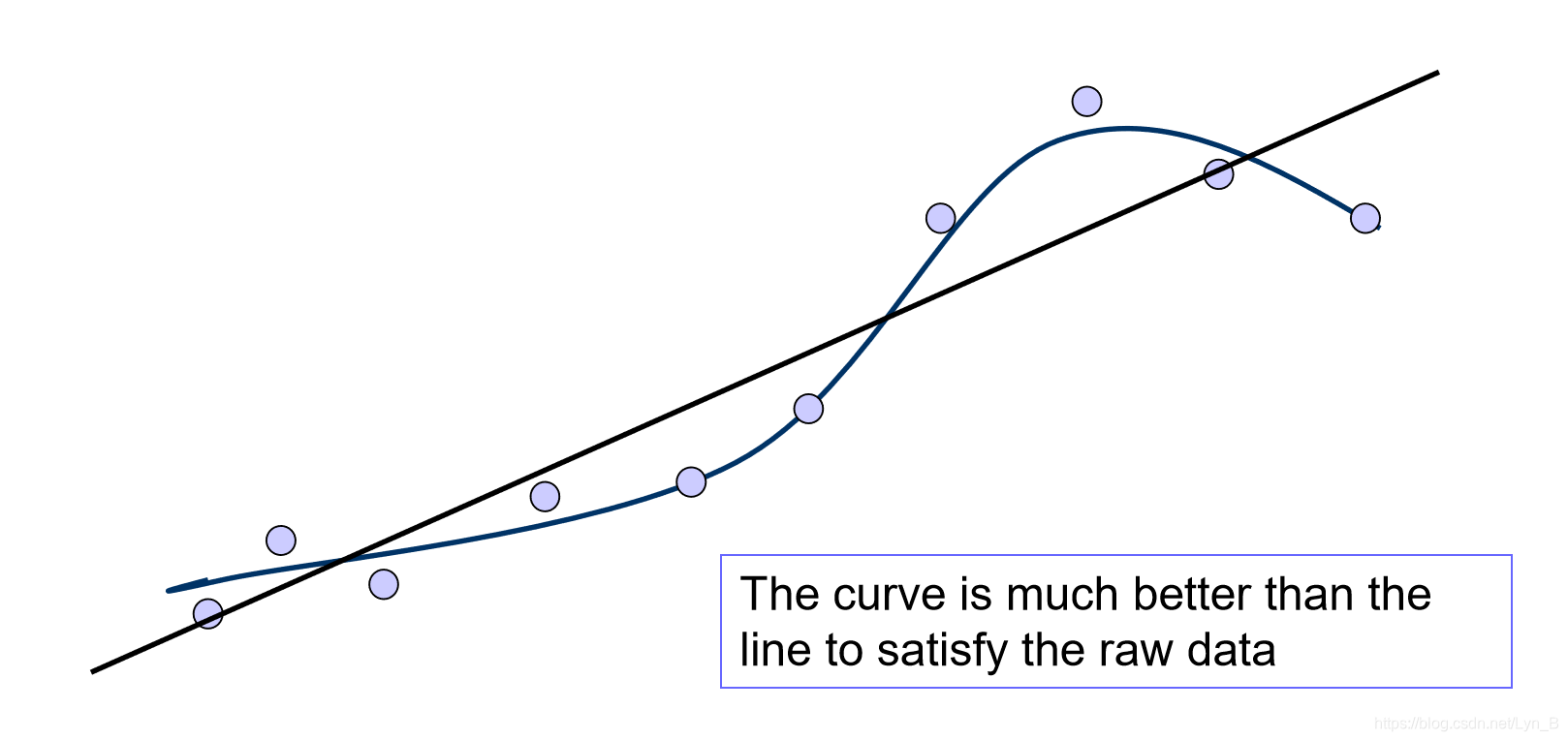
当样本数据非常复杂的时候（没有呈现出比较明显的线性特征），直线的拟合程度较差（最小化后的 $E$ 仍然较大）
这时，引入最小平方曲线（Least Square Curve），通式：
$a_{0} + a_{1}x + a{2}x^{2} + \dots + a_{k}x^{k} \tag{6}$
即一个k阶多项式，同理，当系数向量 $[a_{0} \dots a_{k}]$ 满足：
$\min E = \sum_{i=1}^{n}(f(x_{i}) - y_{i}) \tag{7}$
此时，该曲线即为目标曲线。
同理，可得：
$\left[ \begin{matrix} 1 & x_{1} & x_{1}^{2} & \dots & x_{1}^{k} \\ 1 & x_{2} & x_{2}^{2} & \dots & x_{2}^{k} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n} & x_{n}^{2} & \dots & x_{n}^{k} \end{matrix} \right] \left[ \begin{matrix} a_{0} \\ a_{1} \\ \vdots \\ a_{k} \end{matrix} \right]= \left[ \begin{matrix} y_{1} \\ y_{2} \\ \dots \\ y_{n} \end{matrix} \right] \tag{8}$
通过求解这个系统可以得到最小二乘曲线。设上面的等式为：
$Y\tag{9}$
则同理左右同乘以 $X$ 的转置，我们可以得到：
$X^{T}X)A = X^{T}Y$
在这里插入图片描述