模拟考 平衡树

描述

平衡树并不是平衡二叉排序树。
这里的平衡指的是左右子树的权值和差距尽可能的小。
给出n个结点二叉树的中序序列w[1],w[2],…,w[n]，请构造平衡树，并给出平衡树的先序序列。
平衡树构造算法如下：
（1）假设平衡树树根为序列中元素i，i左侧所有元素权值和S1=w[1]+w[2]+...+w[i-1],
其右侧所有元素权值和S2=w[i+1]+w[i+2]+...w[n]。在选择树根i时要求让S1-S2的绝对值最小。
例如5个元素序列 {5 4 1 2 3}，选择4为树根是最合适的，此时左侧权值和5，右侧权值和6，差值绝对值最小。
如选择其他结点为根，左右两侧权值和的差值绝对值会更大。
（2）选定树根i之后，对序列w[1],w[2],...,w[i-1]和w[i+1],w[i+2],...,w[n]分别构造平衡树，
作为树根i的左右子树。

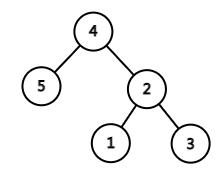
 5个元素序列 {5 4 1 2 3}的平衡树如上图，其先序序列为4 5 2 1 3。

输入格式

第一行一个整数n；
第二行n个正整数表示二叉树的中序序列。

输出格式

n个整数，平衡树的先序序列。
注意：如果选取树根时有两个结点，他们左右两侧权值和的差值绝对值相同，且均为最小值，
我们要求选择编号更小的结点。例如序列（7,6,2,9），选取6或2做树根时，两侧权值和的差值绝对值均为4，
此时要求选择6作为树根。

输入样例

4
7 6 2 9

输出样例

6 7 9 2

build(int left, int right) 函数

1. 终止条件：

   • 若 left > right，说明子树为空，直接返回。
   • 若 left == right，说明子树只有一个节点，输出该节点并返回。

2. 选择最优根节点：

   • 遍历区间 [left, right] 内的每个节点 i，计算其左右子树的权值和。

   • 使用前缀和数组 presum 快速计算区间和：

当 i == left 时：

当前节点 i 是区间 [left, right] 的左边界，其左侧没有元素（左子树为空），因此左子树权值和为 0。

例如，若区间是 [3, 5] 且 i = 3，则左子树区间为 [3, 2]（空）。

当 i > left 时：

左子树的区间为 [left, i-1]，其权值和为 presum[i-1] - presum[left-1]。

例如，若区间是 [2, 5] 且 i = 4，则左子树区间为 [2, 3]，和为 presum[3] - presum[1]。

当 i == right 时：

当前节点 i 是区间 [left, right] 的右边界，其右侧没有元素（右子树为空），因此右子树权值和为 0。

例如，若区间是 [3, 5] 且 i = 5，则右子树区间为 [6, 5]（空）。

当 i < right 时：

右子树的区间为 [i+1, right]，其权值和为 presum[right] - presum[i]。

例如，若区间是 [2, 5] 且 i = 3，则右子树区间为 [4, 5]，和为 presum[5] - presum[3]。

• leftsum = (i==left)? 0 : presum[i-1] - presum[left-1];
  rightsum = (i==right)? 0 : presum[right] - presum[i];
  

• 计算差值绝对值 curd，并更新最小差值 mind 和最优索引 bestindex。

        3.递归构造子树：

• • 输出当前选择的根节点 inorder[bestindex]。
  • 递归处理左子树 build(left, bestindex-1) 和右子树 build(bestindex+1, right)。

#include <iostream>
#include <vector>

using namespace std;

vector<int> inorder;
vector<int> presum;

void build(int left,int right)
{
    if(left>right) return;

    if(left==right)
    {
        cout<<inorder[left]<<" ";
        return;
    }
    int mind=1e9;
    int bestindex=-1;
    for(int i=left;i<=right;i++)
    {
    int leftsum=(i==left)?0:presum[i-1]-presum[left-1];
    int rightsum=(i==right)?0:presum[right]-presum[i];

    int curd=abs(leftsum-rightsum);

    if(curd<mind||(curd==mind&&i<bestindex))
    {
        mind=curd;//更新最小差值
        bestindex=i;//更新下标
    }
    }
cout<<inorder[bestindex]<<" ";
build(left,bestindex-1);
build(bestindex+1,right);
}

int main()
{
    int n;
    cin>>n;

    inorder.resize(n+1);
    presum.resize(n+1,0);

    for(int i=1;i<=n;i++)//求前缀和数组
    {
        cin>>inorder[i];
        presum[i]=presum[i-1]+inorder[i];
    }

    build(1,n);
    return 0;
}