广度优先搜索

参考 : python实现图的广度优先搜素算法并打印最短路径_广度优先算法求最短路径 python-优快云博客

定义

    宽度优先搜索算法（又称广度优先搜索）是最简便的图的搜索算法之一，这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS，属于一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。(来自百度百科)

使用场景

广度优先搜索让你能够找出两样东西之间的最短距离，不过最短距离的含义有很多!使用广 度优先搜索可以:

•   编写国际跳棋AI，计算最少走多少步就可获胜;

•   编写拼写检查器，计算最少编辑多少个地方就可将错拼的单词改成正确的单词，如将

  READED改为READER需要编辑一个地方;

•   根据你的人际关系网络找到关系最近的医生。(来自[图解算法])

实现

在下面有向图中找出A点到L点的最短路径

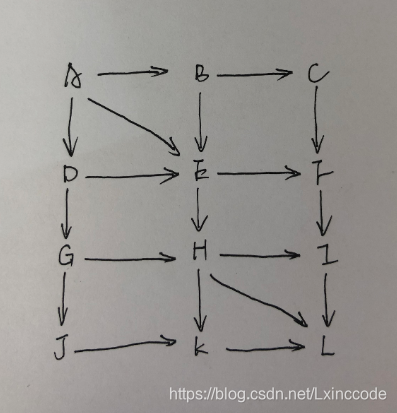
用到的数据结构:

• 队列
• 列表(数组、链表)
• 字典(散列表)

Python代码如下:

# -*- coding:utf-8 -*-
from collections import deque


def init_graph():
    """
    表示一个有向图
    :return:
    """
    graph = dict()
    graph['A'] = ['B', 'D', 'E']
    graph['B'] = ['C', 'E']
    graph['C'] = ['F']
    graph['D'] = ['E', 'G']
    graph['E'] = ['F', 'H']
    graph['F'] = ['I']
    graph['G'] = ['H', 'J']
    graph['H'] = ['I', 'K', 'L']
    graph['I'] = ['L']
    graph['J'] = ['K']
    graph['K'] = ['L']
    graph['L'] = []
    return graph


def search(graph, start, target):
    # 检索队列
    search_queue = deque()
    search_queue += graph[start]
    # 把起点的子节点加入队列
    searched = [start]
    while search_queue:
        # 取出队列的第一个节点
        left = search_queue.popleft()
        # 是否已检索
        if left not in searched:
            if left == target:
                searched.append(left)
                print('->'.join(append_path(searched, graph)))
                break
            else:
                # 把改节点的子节点加入队列
                search_queue += graph[left]
                # 把该节点标记为已检索
                searched.append(left)


def append_path(searched, graph):
    """
    1.取出已检索的节点集合的最后一个节点
    2.遍历已检索的节点集合,根据检索顺序找出第一个子节点含有最后一个节点的节点,把该节点定义为最后节点的父节点
    3.再次遍历已检索的节点集合,检索上步骤找到的节点,寻找第一个子节点含有该节点的接口,重复此操作直至找到的父节点为起点

    :param searched: 已检索的节点集合
    :param graph: 图
    :return:
    """
    target = searched[-1]
    path = [target]
    while target != searched[0]:
        for i in searched:
            if target in graph[i]:
                target = i
                path.append(i)
                break
    return path[::-1]


if __name__ == '__main__':
    graphs = init_graph()
    search(graphs, 'A', 'L')

END。