多源数据融合中权重不再靠感觉！熵权法帮你科学量化指标重要性

在数据分析和多指标评价中，我们经常遇到这样的困扰：

“这些指标哪个更重要？权重怎么分配？”

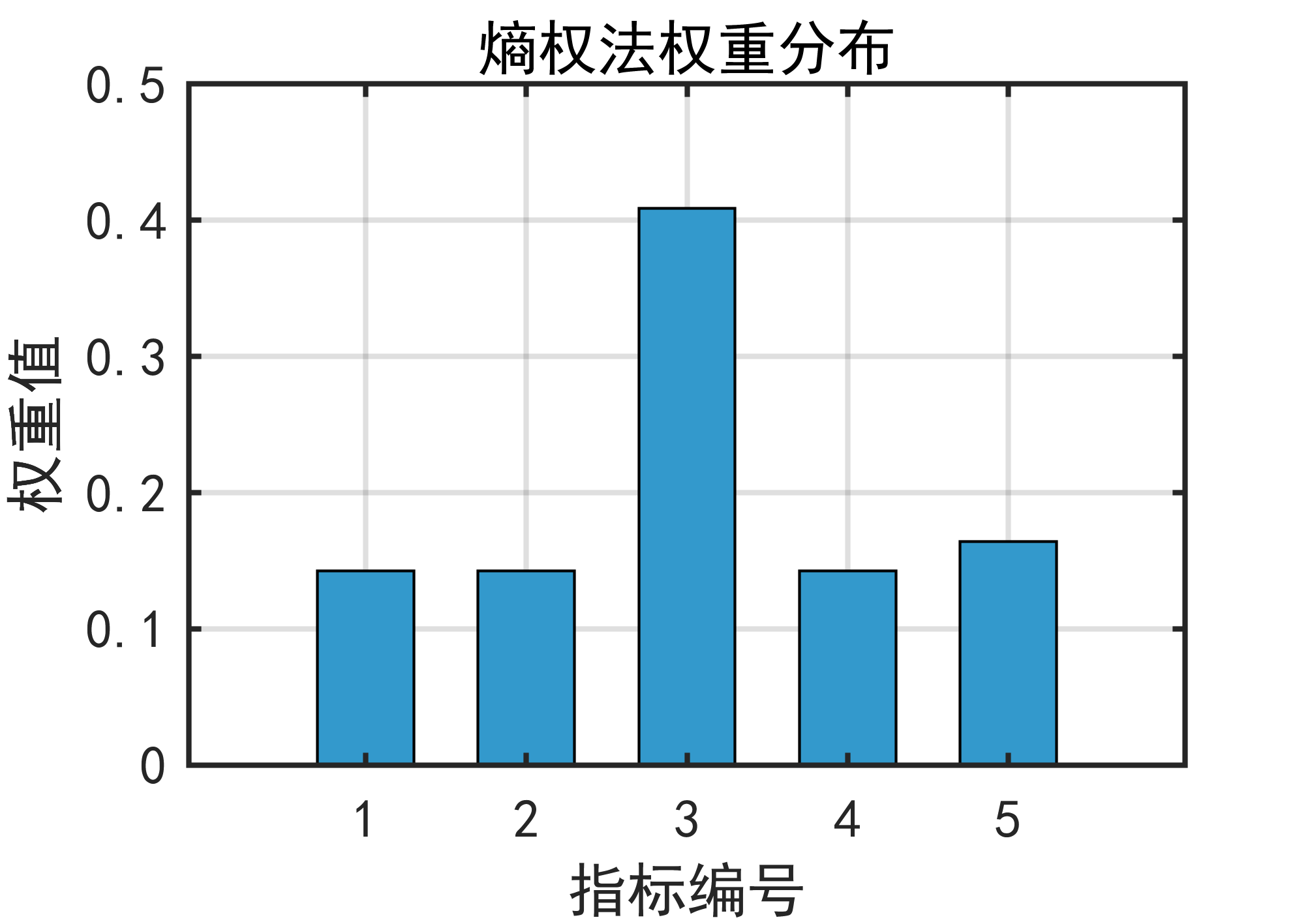
随意赋权容易偏颇，今天我们来聊聊一个经典方法——熵权法（Entropy Weight Method），让数据自己告诉你谁重要💡。代码获取见文末。

1️⃣ 熵权法是什么？

熵权法是一种客观赋权方法，基于信息熵的概念：

• 信息熵衡量的是指标的不确定性或混乱程度。

• 指标离散度越大 → 信息量越多 → 权重越高

• 指标趋于一致或变化小 → 信息量少 → 权重低

通俗来说：

“指标越能区分样本，它就越重要。”

2️⃣ 熵权法算法原理

Step 1️⃣ 数据标准化

• 不同指标量纲不同，需要归一化（0~1）处理：

• 使得所有指标在同一量纲下比较。

Step 2️⃣ 计算指标比例

• 对每个指标计算样本在该指标下的比例

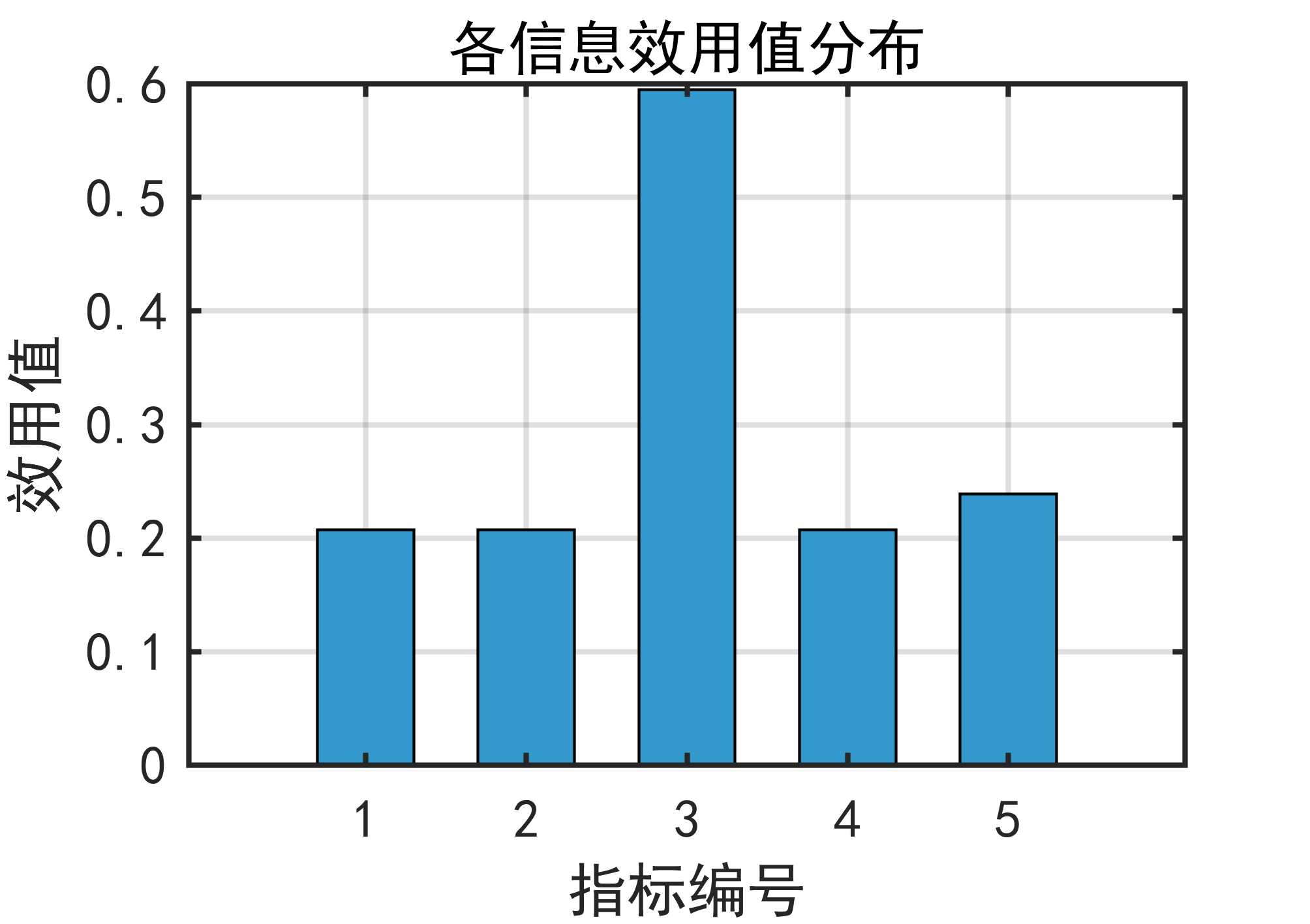
Step 3️⃣ 计算指标熵值 EjE_jEj​

• 熵值反映指标的信息分布均匀程度

• 熵值越大 → 信息越分散 → 区分能力低

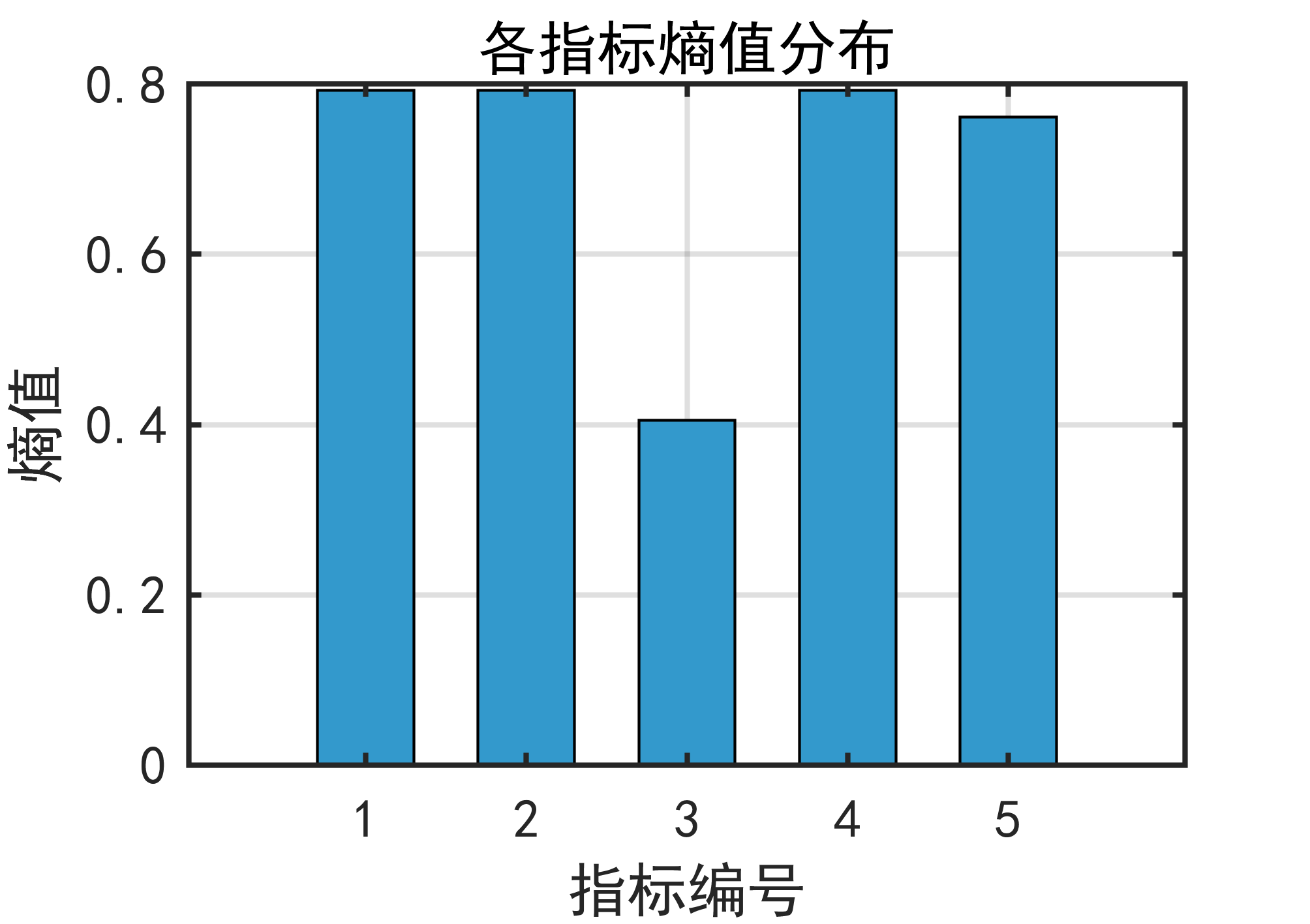
Step 4️⃣ 计算指标权重 wjw_jwj​

• 根据熵值计算指标的“信息量”

• 归一化得到权重

• 权重越高，说明该指标对区分样本的贡献越大

3️⃣ 熵权法特点

特点	说明
客观性强	不依赖专家打分，数据驱动
信息量衡量	指标离散度越大 → 权重越高
操作简单	仅需标准化、熵值计算即可
广泛适用	多指标评价、综合评分、绩效考核等

💡小提示：

• 熵权法强调“信息量”，并不是越变化大就一定越重要，还需结合实际背景

• 可与AHP等主观赋权方法结合，形成“主客观结合权重法”，更科学

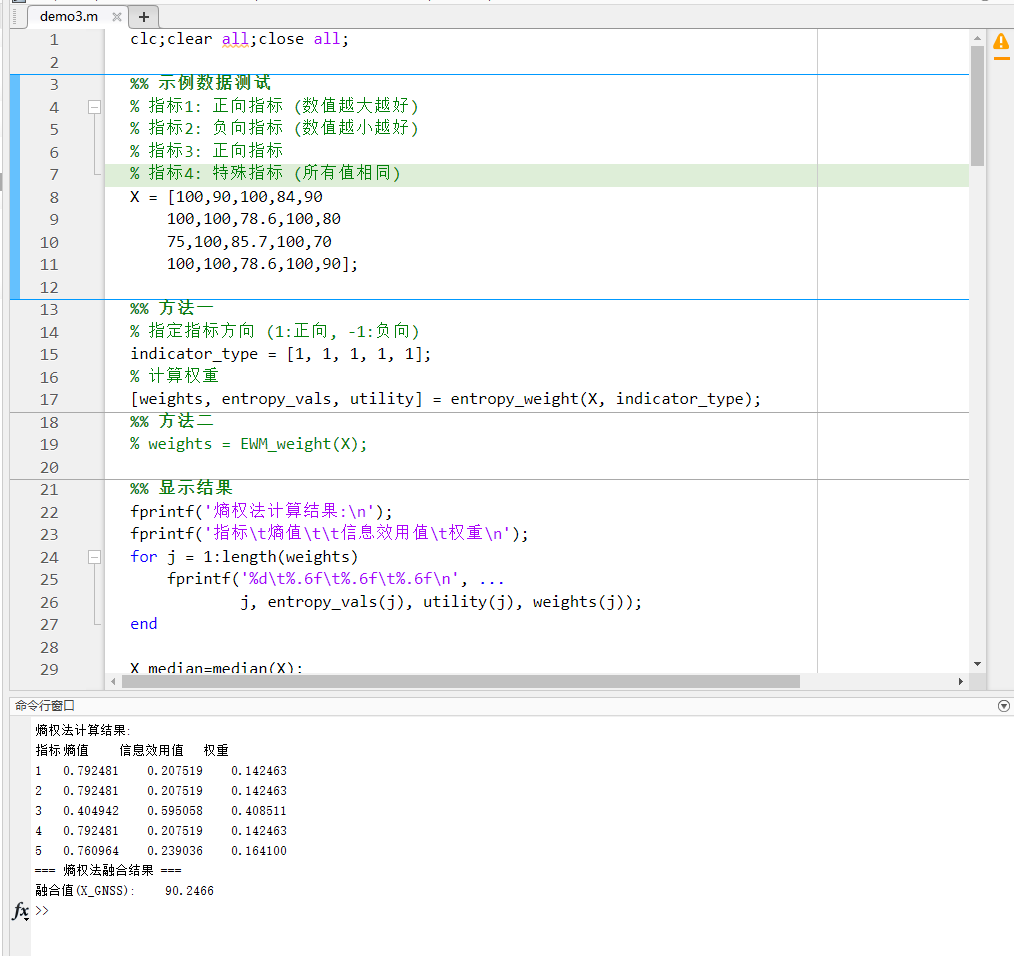
4️⃣ 应用示例

假设评价城市综合竞争力，有指标 GDP、教育水平、环境质量、创新能力：

1. 数据标准化

2. 计算每个指标的样本比例 pijp_{ij}pij​

3. 计算熵值 EjE_jEj​ → 得到每个指标的信息量 dj=1−Ejd_j = 1 - E_jdj​=1−Ej​

4. 归一化 → 得到每个指标权重 wjw_jwj​

💥结果告诉你：

• 离散度大、差异明显的指标 → 权重高 → 贡献大

• 数据趋于一致的指标 → 权重低 → 区分能力弱

💥总结
熵权法核心理念：

“能区分样本的指标最重要”

简单、科学、客观，是多指标决策和评价的利器。

✨ 代码获取

熵权法：