python-leetcode-883. 三维形体投影面积

883. 三维形体投影面积 - 力扣（LeetCode）

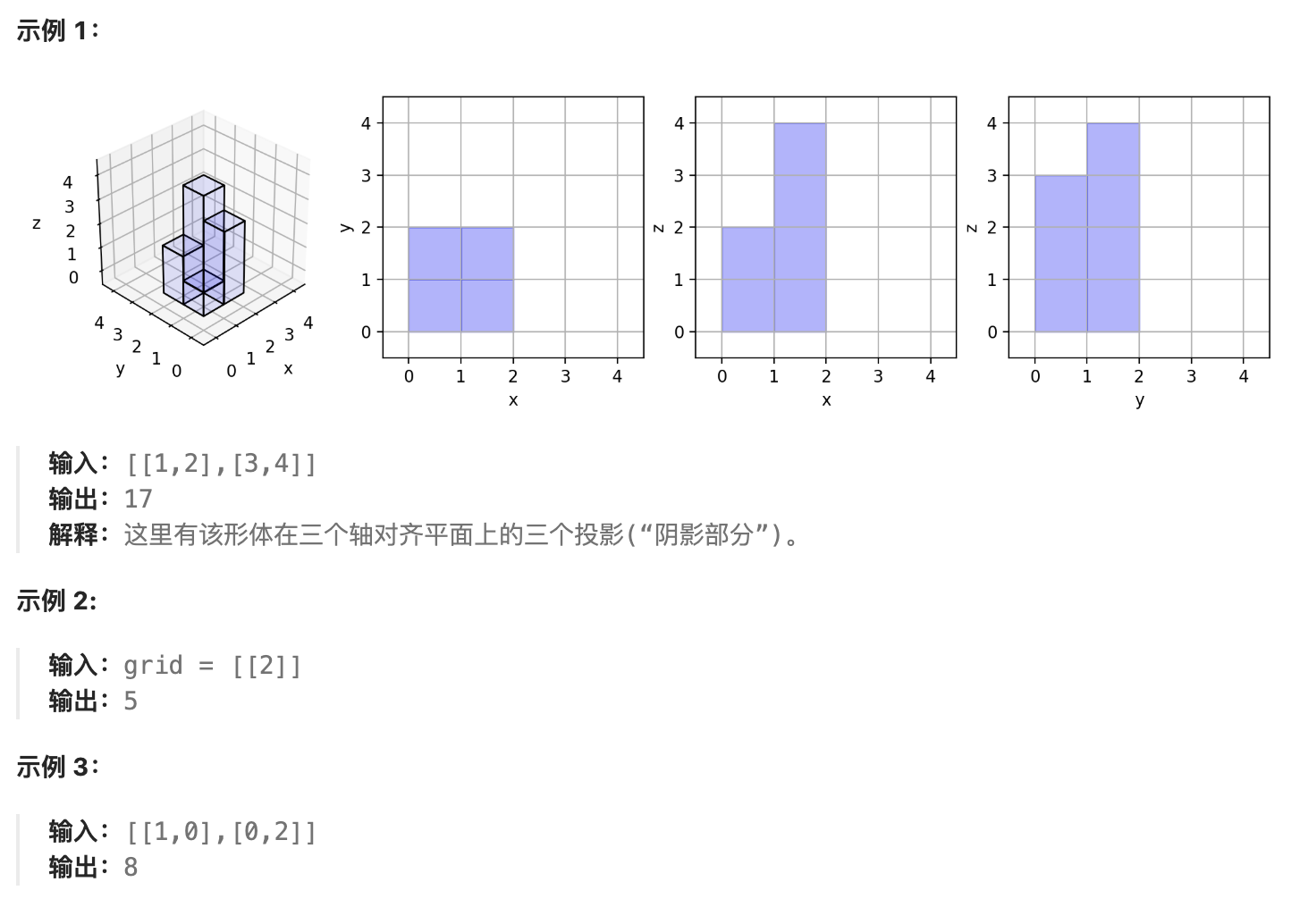
可以通过以下方式计算三个投影的总面积：

1. XY 平面（俯视图）：

   • 任何 grid[i][j] > 0 的位置都会在 XY 平面上留下一个影子。

   • 影子的面积就是 grid[i][j] > 0 的单元格的数量。

2. YZ 平面（侧视图）：

   • 计算每一列的最大值，即 max(grid[i][j]) 对于所有 i。

   • 影子的面积是这些最大值的总和。

3. ZX 平面（正视图）：

   • 计算每一行的最大值，即 max(grid[i])。

   • 影子的面积是这些最大值的总和。

代码实现如下：

def projectionArea(grid):
    n = len(grid)
    xy_area = sum(1 for i in range(n) for j in range(n) if grid[i][j] > 0)
    yz_area = sum(max(grid[i][j] for i in range(n)) for j in range(n))
    zx_area = sum(max(row) for row in grid)
    
    return xy_area + yz_area + zx_area

复杂度分析：

• xy_area 需要遍历整个 grid，时间复杂度 O(n²)。

• yz_area 需要遍历 grid 的每一列，时间复杂度 O(n²)。

• zx_area 需要遍历 grid 的每一行，时间复杂度 O(n²)。

总的时间复杂度是 O(n²)，对于 n ≤ 50 的网格可以高效运行。

示例：

grid = [[1,2],[3,4]]
print(projectionArea(grid))  # 输出: 17

希望这能帮到你！😊