python-leetcode-783. 二叉搜索树节点最小距离

783. 二叉搜索树节点最小距离 - 力扣（LeetCode）

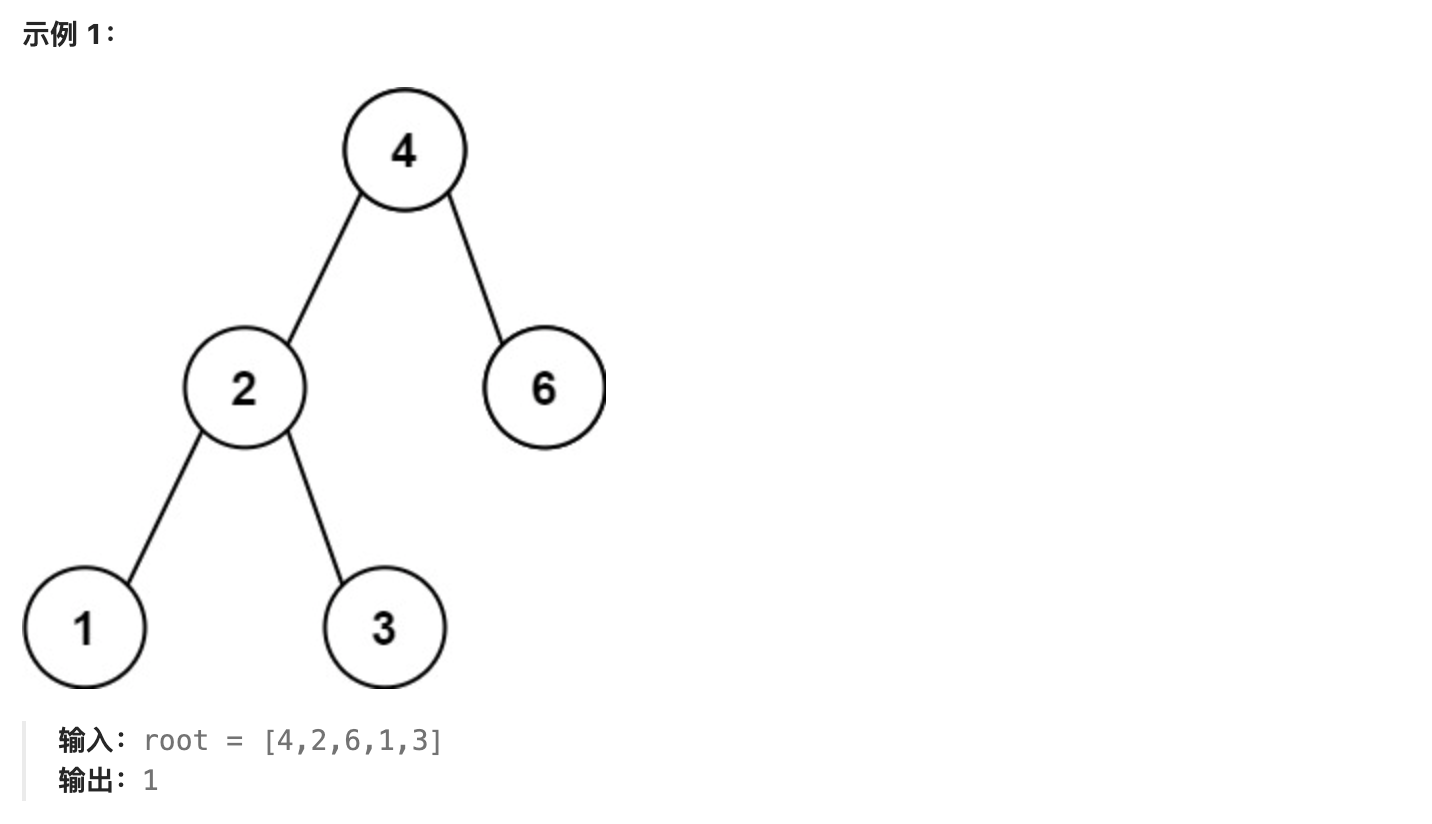
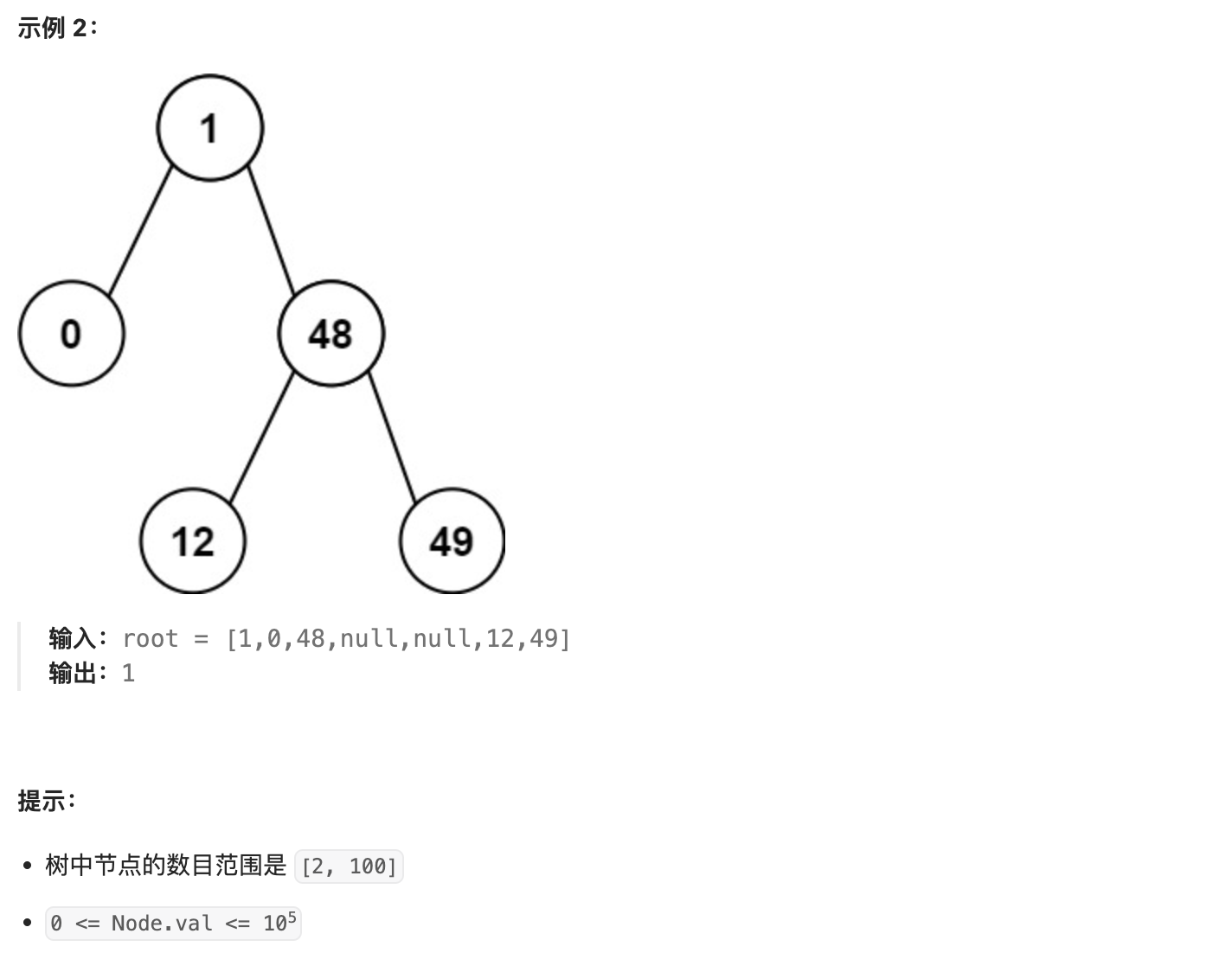
可以使用 中序遍历 来解决这个问题，因为二叉搜索树（BST）的中序遍历结果是一个递增的有序序列。在遍历的过程中，我们记录前一个节点的值，并计算当前节点与前一个节点的差值，从而求出最小差值。

Python 代码实现

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def getMinimumDifference(self, root: TreeNode) -> int:
        self.prev = None  # 记录前一个节点
        self.min_diff = float('inf')  # 记录最小差值

        def inorder(node):
            if not node:
                return
            inorder(node.left)  # 递归左子树
            if self.prev is not None:  # 计算当前节点与前一个节点的差值
                self.min_diff = min(self.min_diff, node.val - self.prev)
            self.prev = node.val  # 更新前一个节点的值
            inorder(node.right)  # 递归右子树

        inorder(root)
        return self.min_diff

方法解析

1. 中序遍历 BST：BST 的中序遍历会得到一个递增的序列。

2. 比较相邻节点差值：由于是递增的，所以相邻节点的差值就是可能的最小差值。

3. 更新最小值：遍历过程中，维护一个 prev 变量记录上一个节点值，并不断更新 min_diff。

时间 & 空间复杂度

• 时间复杂度：O(N)，因为需要遍历整个 BST。

• 空间复杂度：O(H)，其中 H 是 BST 的高度（递归栈的空间）。

这样，你就可以高效地求出 BST 中最小的节点差值！ 🚀