分类网络可以采用那些损失函数？

分类网络可以采用以下几种常见的损失函数，具体选择取决于任务的类型（如二分类、多分类、不平衡数据分类等）：

---

1. 二分类任务

(1) 二元交叉熵损失（Binary Cross-Entropy Loss）

公式：

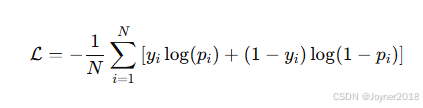
• 适用场景：用于二分类任务。
• 优势：对正负样本平衡时表现良好。

(2) 对数损失（Log Loss）

与二元交叉熵类似，用于二分类问题，常在Logistic回归中使用。

---

2. 多分类任务

(1) 多元交叉熵损失（Categorical Cross-Entropy Loss）

公式：

 

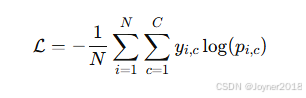
• 适用场景：用于多分类任务。
• 优势：能自然处理多类别标签，预测概率与真实标签的匹配程度直接相关。

(2) 稀疏交叉熵（Sparse Categorical Cross-Entropy）

• 区别：与多元交叉熵类似，但标签可以是稀疏的整数编码（而不是独热编码）。

---

3. 不平衡分类任务

(1) 加权交叉熵（Weighted Cross-Entropy Loss）

公式：

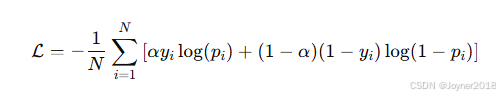
• 适用场景：主要用于处理极度不平衡的数据集，如目标检测中的小目标。
• 参数解释：
  • ：预测的正确类别的概率。
  • ：控制对难分类样本的关注程度。
  • ：类别权重。

---

4. 特定场景的分类任务

(1) KL散度（Kullback-Leibler Divergence）

• 公式：

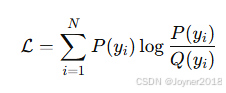
• 适用场景：用于测量两个概率分布之间的差异。

(2) 交叉熵 + KL散度

• 应用于知识蒸馏（Knowledge Distillation）任务中，学生网络学习教师网络的输出。

(3) 对比学习损失（Contrastive Loss）

• 公式：

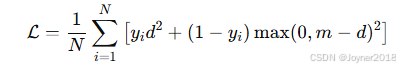
• 适用场景：适用于分类任务中的表示学习和相似性学习。

---

5.其他损失函数

(1) 余弦相似性损失（Cosine Similarity Loss）

• 公式：

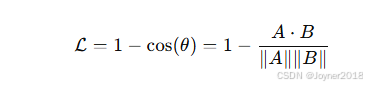
• 适用场景：用于度量向量之间的相似性。

(2) Triplet Loss

• 公式：

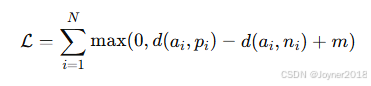
• 适用场景：用于度量学习和嵌入表示。