07 递归

原创已于 2022-02-10 16:12:53 修改 · 258 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2021-12-29 20:59:35 首次发布

算法专栏收录该内容

11 篇文章

订阅专栏

举个生活中的例子：

周末，你带着你女朋友去买奶茶，可是这家店太火爆了，排了老长的队伍。突然，奶茶店给出了一个通知，说，只剩最后100杯了，卖完就没了。

女朋友问你，现在我们所在位置是第几呀？队伍太长了，你不想一个个数一次。于是你问前面的人他是第几个，这样只需要在他的基础上加1，就知道自己是第几了。

但是前面的人也不知道他自己是第几，所以他也问前面的。就这样一个问一个，直到问道了第一个，说我是第一个。然后再这样一个个把数字往后传，直到你前面的人告诉你他是第几，这样你就知道答案了。

这就是一个非常标准的递归求解问题的分析过程，去的过程叫“递“，回来的过程叫”归“。

基本上所有的问题都能用递推公式来表示，刚才的例子就可以这样表示：

$f(n) = f(n-1) + 1$

$f(1) = 1$

f(n)表示你所在位置的数字，f(n-1)表示你前面位置的数字。f(1) =1表示第一个位置的数字是1.

有了递推公式，我们就能把他改写成代码：

int f(int n) {
  if (n == 1) return 1;
  return f(n-1) + 1;
}

一、递归需要满足的三个条件

1、一个问题的解可以分为多个问题的解

可以把一个问题分为一个个数据规模更小的子问题，比如前面的例子。

2、子问题的求解思路完全样

比如前面的例子，除了第一个，每个人求自己位置的办法都一样。

3、存在递归终止条件

这是最重要的一个条件。把问题分为子问题，再把子问题一层层分解下去，必须得有终止条件，不能无限制。

比如刚才f(1) =1 就是终止条件。

二、如何编写递归代码

最关键的就是找出递推公式和终止条件。

比如一个常见的算法题，爬楼梯：

假如有n阶台阶，你每次只能跨一个台阶或者2个台阶，那么走这n个台阶有多少种走法？

比如一个台阶只有一种走法。2个台阶可以是1 1和2，两种走法。3阶台阶可以是1 1 1，1 2，2 1这三种走法。。。。

分析：

当你走到第n阶台阶的时候，最后一步你只会有2种情况走上来。要么是跨了一个台阶上到第n个台阶，要么是跨了2个台阶上来。

当你是跨了跨一个台阶上来的时候，只需要知道n-1个台阶的时候的走法数。跨了2个台阶，只需要知道n-2个台阶的走法数。

可以表示为f(n) = f(n-1) + f(n-2)

也就是第n个台阶的走法= n-1个台阶位置的走法 + n-2个台阶位置的走法。

终止条件：

f(1) = 1, f(2) = 2

所以合起来就是：

f(n) = f(n-1) + f(n-2)
f(1) = 1
f(2) = 2

代码表示：

int f(int n) {
  if (n == 1) return 1;
  if (n == 2) return 2;
  return f(n-1) + f(n-2);
}

总结：

人的大脑适合平铺直叙的思维方式，不适合递归这种思维，所以不要用大脑去一层层嵌套下去，我们只需要总结递推公式就好。只有找到终止条件，以及问题与子问题之前的公式就能写出递归代码了。

三、递归要警惕栈溢出

前面栈章节说过，程序调用会使用栈来存储临时变量，每调用一个函数，就会将临时变量封装为栈帧放压入内存栈（java中叫做java虚拟机栈），等函数执行完返回，才会出栈。这种空间一般都不大，很容易造成溢出。

如何避免：

1、一定要有终止条件 2、增加变量，每递归一次就+1。然后限制递归深度。

四、递归要警惕重复计算

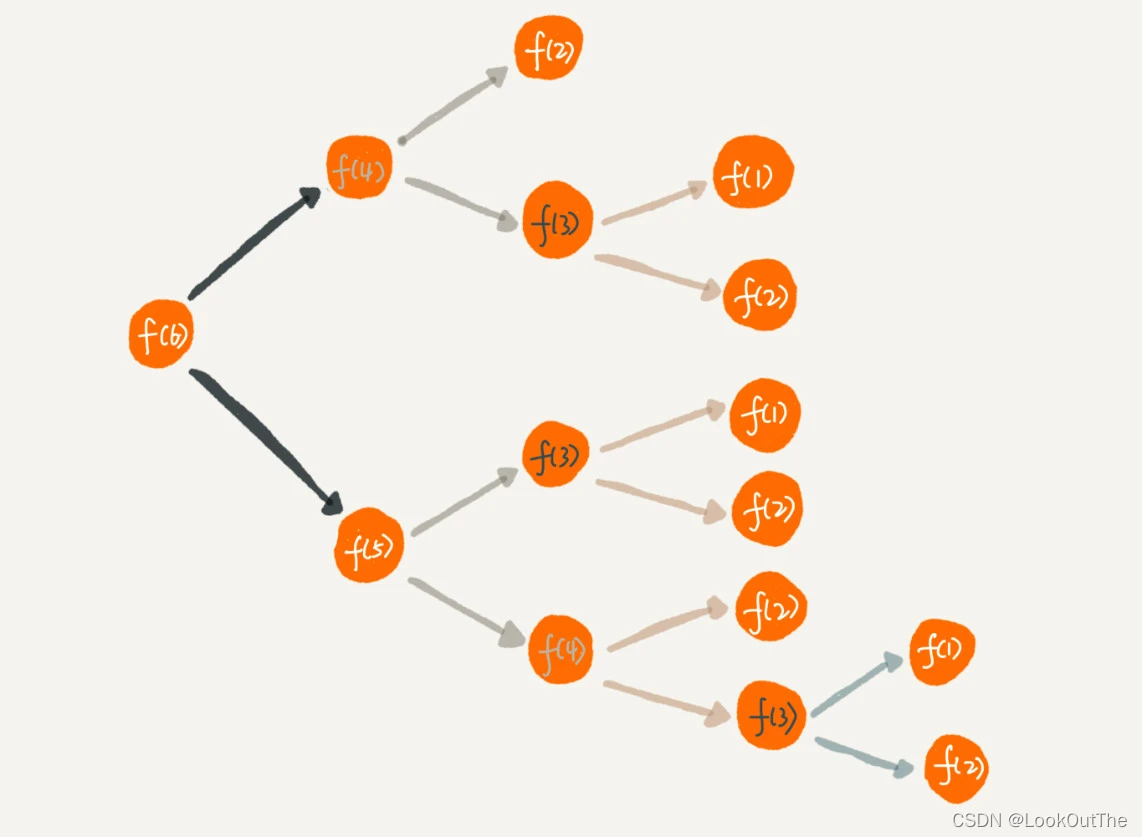
之前的代码中，如上图，我们要计算f(6)就得先计算f(5)和f(4)。计算f(5)的时候还得再计算一次f(4)。有很多重复运算。

为了避免重复运算，我们可以把计算后的结果保存下来。照着这个思路，我们改写下代码：


public int f(int n) {
  if (n == 1) return 1;
  if (n == 2) return 2;
  
  // hasSolvedList可以理解成一个Map，key是n，value是f(n)
  if (hasSolvedList.containsKey(n)) {
    return hasSolvedList.get(n);
  }
  
  int ret = f(n-1) + f(n-2);
  hasSolvedList.put(n, ret);
  return ret;
}

在考虑递归的时间复杂度，我们要考虑递归调用，所以前面排队买奶茶的例子中，时间复杂度是O(n)

五、如何将递归代码改为非递归

第一个排队：


int f(int n) {
  int ret = 1;
  for (int i = 2; i <= n; ++i) {
    ret = ret + 1;
  }
  return ret;
}

第二个爬楼梯：


int f(int n) {
  if (n == 1) return 1;
  if (n == 2) return 2;
  
  int ret = 0;
  int pre = 2;
  int prepre = 1;
  for (int i = 3; i <= n; ++i) {
    ret = pre + prepre;
    prepre = pre;
    pre = ret;
  }
  return ret;
}

是不是所有的递归都能改为非递归那？

笼统的讲：是的，因为递归本身就是借助栈来实现的，如果自己实现栈，任何代码看上去都会是非递归的。不过这样徒然增加复杂度，没有改变递归的本质。