数据结构学习笔记（四）矩阵、串和广义表

---

1. 前言

本系列笔记基于 清华大学出版社的《数据结构：用面向对象方法与C++语言描述》第二版进行学习。

2. 多维数组

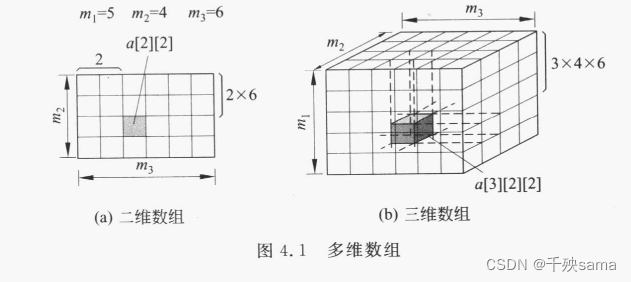
图片易于理解

2.1 特殊矩阵

2.2 稀疏矩阵

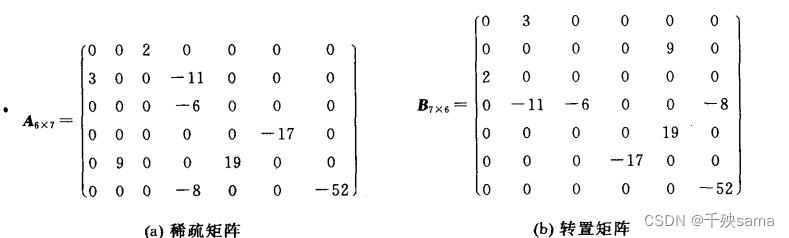
2.2.1 三元组存储稀疏矩阵

上图两矩阵中的三元组，用一元数组存储，使用行（row）列（col）作为标识符存储值数据。

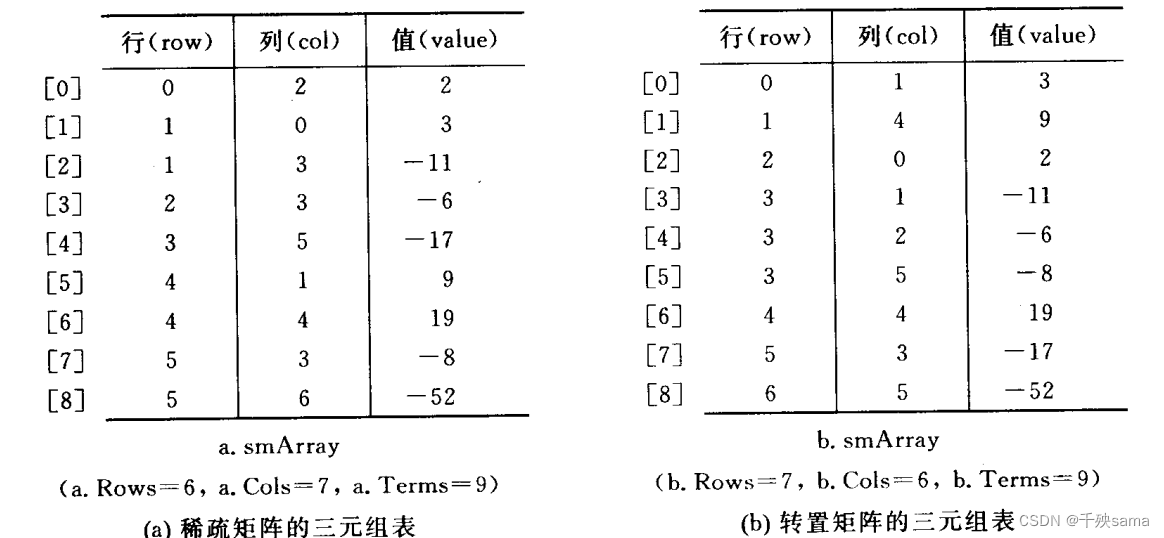
2.2.2 稀疏矩阵的转置

简单的来讲，就是将矩阵中元素的row和col替换一下，第一种方法就是循环整个数组，将数组的所有元素的行和列交换。

SparseMatrix SparseMatrix::Transpose()
{
    SparseMatrix b(maxTerms);
    b.Rows = Cols;                      // 将矩阵的行列调换
    b.Cols = Rows;
    b.Terms = Terms;                
    if (Terms > 0) {
        int k, i, CurrentB = 0;         // 存放位置指针
        for (k = 0; k < Cols; k++)                  // 相当于从列开始找，如果这一列中有元素的col == 列数k，则进行反转
            for(i=0;i<Terms;i++)
                if (smArray[i].col == k) {
                    b.smArray[CurrentB].row = smArray[i].col;
                    b.smArray[CurrentB].col = smArray[i].row;
                    b.smArray[CurrentB].value = smArray[i].value;
                    CurrentB++;
                }
    }
    return b;
}

2.2.3 快速转置的方法

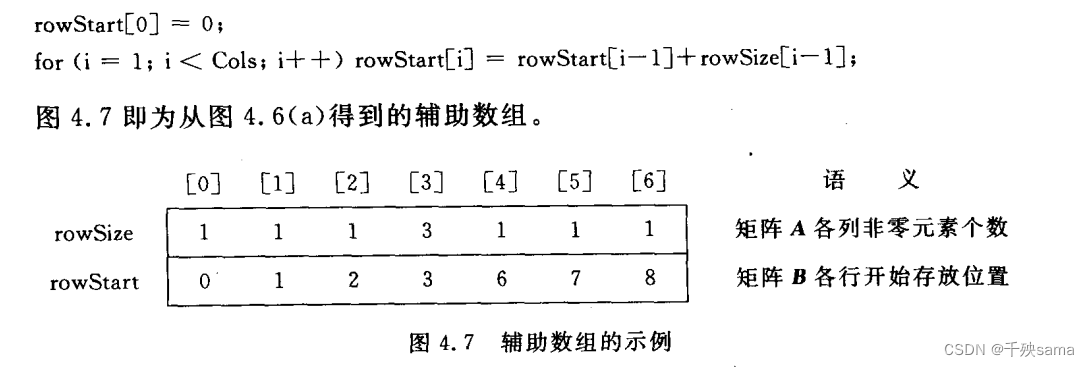
上诉方法进行转置做的复杂度太大，效率太低，可以通过两个新的数组进行辅助。

分别是存储每列的非零元素个数的rowSize[]，

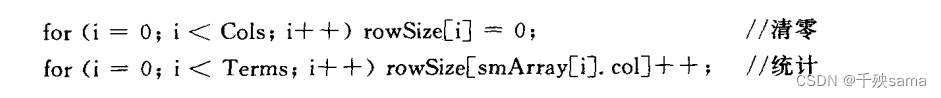
和存储这一列是从哪一个元素开始的rowStart[]。

SparseMatrix SparseMatrix::FastTranspose()
{
    int* rowSize = new int[Cols];
    int* rowStart = new int[Cols];
    SparseMatrix b(maxTerms);
    b.Rows = Cols;
    b.Cols = Rows;
    b.Terms = Terms;            // 给转置后的矩阵赋值

    if (Terms > 0) {
        int i, j;
        for (i = 0; i < Cols; i++) rowSize[i] = 0;
        for (i = 0; i < Terms; i++) rowSize[smArray[i].col]++;  // 循环存储三元组的数组，并根据元组中col的值，将对应的rowSize[col] + 1。
        rowStart[0] = 0;
        for (int i = 1; i < Cols; i++)
            rowStart[i] = rowStart[i - 1] + rowSize[i - 1];             // 上一列中的开始数字和上一列中元素的个数相加得到下一列元素的开始
        for (int i = 0; i < Terms; i++) {
            j = rowStart[smArray[i].col];                                       // 遍历三元组，获得该列的开始坐标
            b.smArray[j].row = smArray[i].col;
            b.smArray[j].col = smArray[i].row;
            b.smArray[j].value = smArray[i].value;
            rowStart[smArray[i].col]++;
            
        }
    }
    delete[] rowSize; 
    delete[] rowStart;
    return b;
}

这书写的真的复杂，感觉很简单的东西一定要写这么复杂？

2.2.4 稀疏矩阵的实现

#include <iostream>

using namespace std;

const int DefaultSize = 100;

struct Trituple {
    int row, col;
    int value;
    Trituple& operator = (Trituple& x) {
        row = x.row;
        col = x.col;
        value = x.value;
    }
};

class SparseMatrix {

    friend ostream& operator<<(ostream& out, SparseMatrix& M);      //输出M
    friend istream& operator>>(istream& in, SparseMatrix& M);
private:
    int Rows;               // 稀疏矩阵总行数 （整个矩阵）
    int Cols;                 // 稀疏矩阵总列数   （整个矩阵）
    int Terms;              // 稀疏矩阵非0元素个数（可以理解为如果打印Terms个数据，就打印数组中前Terms个数据）
    Trituple* smArray;
    int maxTerms;       //  三元组个数的最大值？
public:
    SparseMatrix(int maxSz = DefaultSize);                  
    SparseMatrix(SparseMatrix& x);                              
    ~SparseMatrix() { delete[] smArray; }
    SparseMatrix Transpose();                                // 转置运算
    SparseMatrix FastTranspose();
    SparseMatrix Add(SparseMatrix& b);              // 矩阵相加
    SparseMatrix Multiplies(SparseMatrix& b);     // 矩阵相乘
};


int main()
{
    std::cout << "Hello World!\n";
}

SparseMatrix::SparseMatrix(int maxSz)
{
    if (maxSz < 1) {
        cout << "error maxSz when allocate memory!" << endl;
        exit(1);
    }
    smArray = new Trituple[maxSz];
    if (smArray == NULL) { cout << "error when allocate memory!" << endl;  exit(1); }
    Rows = Cols = Terms = 0;
}

SparseMatrix::SparseMatrix(SparseMatrix& x)
{
    Rows = x.Rows;
    Cols = x.Cols;
    Terms = x.Terms;
    maxTerms = x.maxTerms;
    smArray = new Trituple[maxTerms];
    if (smArray == NULL) { cout << "error when allocate memory!" << endl; exit(1); }
    for (int i = 0; i < x.Terms; i++) smArray[i] = x.smArray[i];
}

SparseMatrix SparseMatrix::Transpose()
{
    SparseMatrix b(maxTerms);
    b.Rows = Cols;                      // 将矩阵的行列调换
    b.Cols = Rows;
    b.Terms = Terms;                
    if (Terms > 0) {
        int k, i, CurrentB = 0;         // 存放位置指针
        for (k = 0; k < Cols; k++)                  // 相当于从列开始找，如果这一列中有元素的col == 列数k，则进行反转
            for(i=0;i<Terms;i++)
                if (smArray[i].col == k) {
                    b.smArray[CurrentB].row = smArray[i].col;
                    b.smArray[CurrentB].col = smArray[i].row;
                    b.smArray[CurrentB].value = smArray[i].value;
                    CurrentB++;
                }
    }
    return b;
}

SparseMatrix SparseMatrix::FastTranspose()
{
    int* rowSize = new int[Cols];
    int* rowStart = new int[Cols];
    SparseMatrix b(maxTerms);
    b.Rows = Cols;
    b.Cols = Rows;
    b.Terms = Terms;            // 给转置后的矩阵赋值

    if (Terms > 0) {
        int i, j;
        for (i = 0; i < Cols; i++) rowSize[i] = 0;
        for (i = 0; i < Terms; i++) rowSize[smArray[i].col]++;  // 循环存储三元组的数组，并根据元组中col的值，将对应的rowSize[col] + 1。
        rowStart[0] = 0;
        for (int i = 1; i < Cols; i++)
            rowStart[i] = rowStart[i - 1] + rowSize[i - 1];             // 上一列中的开始数字和上一列中元素的个数相加得到下一列元素的开始
        for (int i = 0; i < Terms; i++) {
            j = rowStart[smArray[i].col];                                       // 遍历三元组，获得该列的开始坐标
            b.smArray[j].row = smArray[i].col;
            b.smArray[j].col = smArray[i].row;
            b.smArray[j].value = smArray[i].value;
            rowStart[smArray[i].col]++;
            
        }
    }
    delete[] rowSize; 
    delete[] rowStart;
    return b;
}





SparseMatrix SparseMatrix::Add(SparseMatrix& b)
{
    return SparseMatrix();
}

SparseMatrix SparseMatrix::Multiplies(SparseMatrix& b)
{
    return SparseMatrix();
}

ostream& operator<<(ostream& out, SparseMatrix& M)
{
    out << "rows =" << M.Rows << endl;
    out << "cols=" << M.Cols << endl;
    out << "Nonzero terms = " << M.Terms << endl;
    for (int i = 0; i < M.Terms; i++) {
        out << "M[" << M.smArray[i].row << "][" << M.smArray[i].col << "]=" << M.smArray[i].value << endl;
        return out;
    }
}

istream& operator>>(istream& in, SparseMatrix& M)
{
    cout << "Enter number of rows, columns and terms" << endl;
    in >> M.Rows >> M.Cols >> M.Terms;
    if (M.Terms > M.maxTerms) {
        cout << "Number of rows overflow" << endl; exit(1); 
    }
    for (int i = 0; i < M.Terms; i++) {
        cout << "Enter row, column, and value of term : " << i + 1 << endl;
        in >> M.smArray[i].row >> M.smArray[i].col >> M.smArray[i].value;
    }
    return in;
}

3 字符串

3.1 字符串的概念

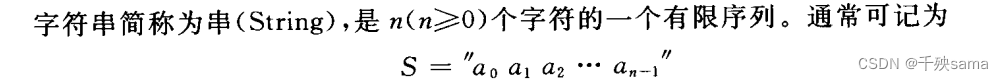
3.2 关于字符串的库函数

3.2.1 strcpy 字符串复制

int strcpy(char * string1, char * string2)

将字符串string2的值复制到string1。

char str1[] = "word1";
char str2[] = "word2";
strcpy(str1,str2);

运行结果

str1 = "word2";
str2 = "word2";

3.2.2 strncpy 字符串部分复制

int strncpy(char *string1, char *string2, int n)

用字符串string2的前n个字符覆盖字符串string1的前n个字符。

char str1[] = "hello";
char str2[] = "World";
strncpy(str1,str2,2)

运行结果

str1 = "wollo";
str2 = "world";

3.2.3 strcat 字符串连接

int strcat(char *string1, char string2)

将字符串string2连接到string1后面，存于string1中，string2不改变

char str1[] = "Tsing";
char str2[] = "hua";
strcat(str1, str2);

运行结果

str1 = "Tsinghua"
str2 = "hua"

3.2.4 strncat 将特定数量字符串连接到另一个

int strncat(char *string1, char string2, int n)

将字符串string2的前n个字符连接到字符串string1之后，存在string1中，string2中的内容不变。

char str1[] = "Tsing";
char str2[] = "hua";
strcat(str1, str2，2);

运行结果

str1 = "Tsinghu"
str2 = "hua"

3.2.5 _strdup 预先配置内存，将字符串存入该内存中

char _strdup(char *string1)

为字符串string1 分配内存空间，并存储string1到其中，并返回内存地址。

char *p, str[] = "Beijing"
p = _strdup(str)

3.2.6 strchr 在给定字符串中搜寻指定字符

char strchr(char *string1, char *ch)

在string1中搜索字符串ch，并返回指向string1中ch的指针，搜索失败返回null

char str1[] = "Tsing";
char str2[] = "sing";
char* add = strrchr (str1, str2);

3.2.7 strcspn 在给定字符串中搜寻某个字符串第一次出现的位置

int strcspn(char *string1, char *ch)

查找字符串string1中ch首次出现的位置（从0开始计数）

char str1[] = "Tsing";
char str2[] = "sing";
int number = strcspn (str1, str2);

number的值：

number = 1;

3.2.8 strrchr 在给定字符串中搜寻某个字符串最后一次出现的位置

char* strrchr (char *string1, char *ch)

查找字符串string1中ch最后一次出现的地址

char str1[] = "TsingTsing";
char str2[] = "sing";
char * ch = strcspn (str1, str2);

3.2.9 strpbrk 在两个字符串中寻找首次共同出现的字符

char *strpbrk(char *string1, char *ch)

返回两个字符串中首次首次共同出现的字符，并返回string1中该字符的地址

char str1[] = "Tsing";
char str2[] = "s";
char *ch = strcspn (str1, str2);

ch指向str1的“s"

3.2.10 strstr 在两个字符串中寻找首次共同出现的字符串

int strcspn(char *string1, char *ch)

查找字符串string1中ch首次出现的位置（从0开始计数）

char str1[] = "Tsing";
char str2[] = "sing";
int number = strcspn (str1, str2);

ch指向str1的“s"

3.2.11 strlen 计算字符串的长度

int strcspn(char *string1)

计算字符串string1中字符的个数，不计算"\0’和分界符" " "

char str1[] = "Tsing";
int number = strcspn (str1, str2);

number = 5

3.2.12 _strnset 在给定字符串按数目替换为指定字符串

char _strnset(char *string1,char ch,int m)

按照指定数目m，将ch替换到string1的前m个字符

char str1[] = "Tsinghua University";
char * p = _strnset (str1, 'x', 9);

p = "xxxxxxxxxUniversity"

3.2.13 strcmp 字符串比较大小

int strcmp(char *string1,char * string2)

比较字符串string1和string2的大小,如果string1>string2，返回<0的int型，string1=string2，返回0，string1<string2，返回>0的int型

char str1[] = "Tsinghua University";
char str2[] = "sing";
int number = strcmp(char *str1,char * str2)

number

number<0;

4 广义表

4.1 广义表的定义与性质

LS称为表名，ai是表中元素，n是表的长度。表的长度不包括“（” 、“）” 和 “，”，a0称为表头，除a0外的所有表元素组成的表称为表尾。
广义表允许表中有表，看几个例子：

性质：
1）有次序性，各表元素按线性序列排序，每个元素最多一个直接前驱，一个直接后继。
2）有长度，表中元素一定，不可能是无限的，可以是空表。
3）有深度，广义表是多层次结构，图中A和B的深度是1，C的深度是2，D的深度是3，E的深度是4，F的深度无限大。

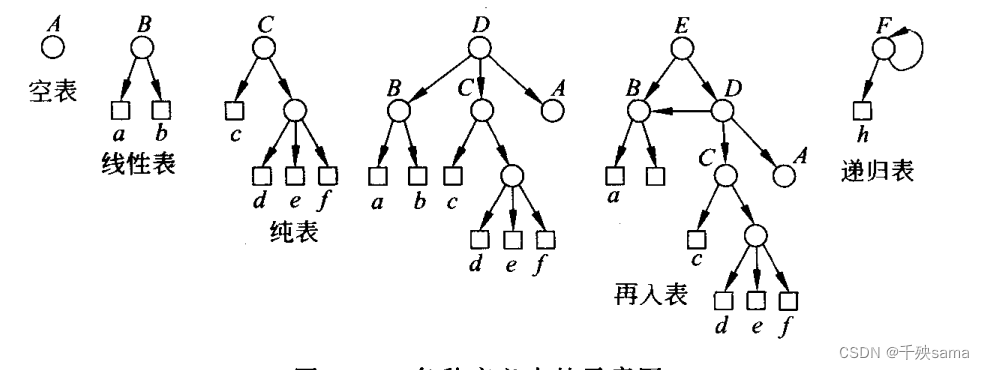
4）可递归，广义表本身可以是自己的子表，如F=（h，F）
5）可共享，广义表可以为其他广义表共享如E=（B,D)

4.2 广义表的表示

一般来讲使用链表存储，
如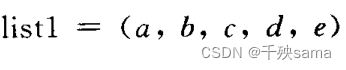

则链表表示为

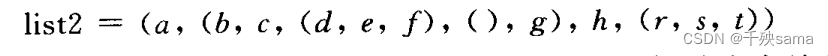
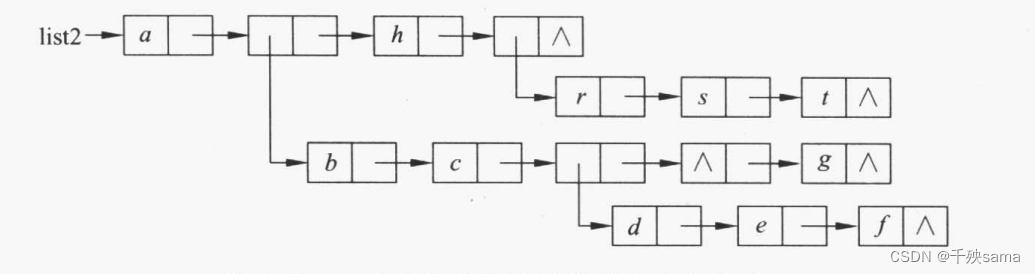
4.3 广义表存储结构的实现

书上写得跟狗屎一样，找了其他地方的广义表存储结构进行理解。

以下内容都来自于广义表的存储结构
表结点

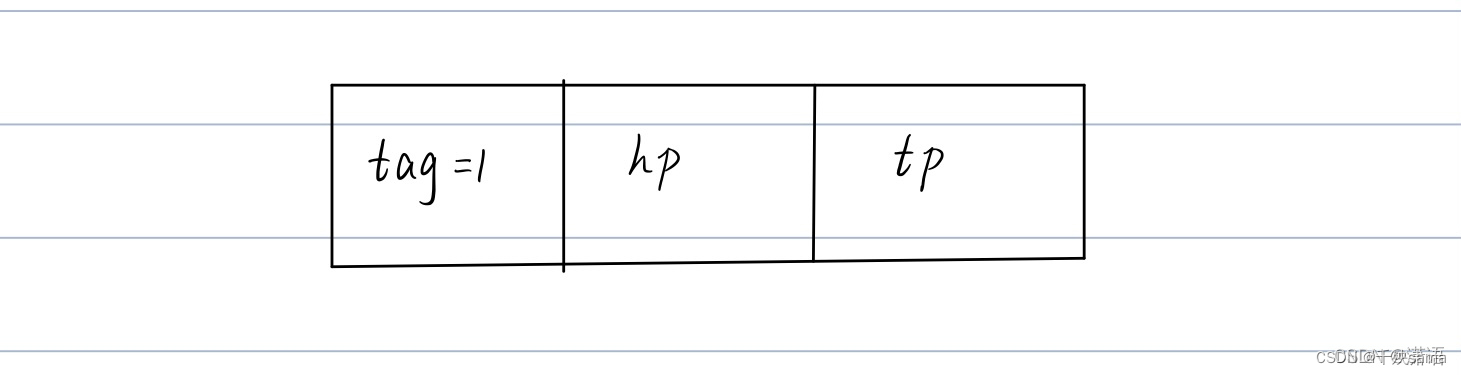
原子结点


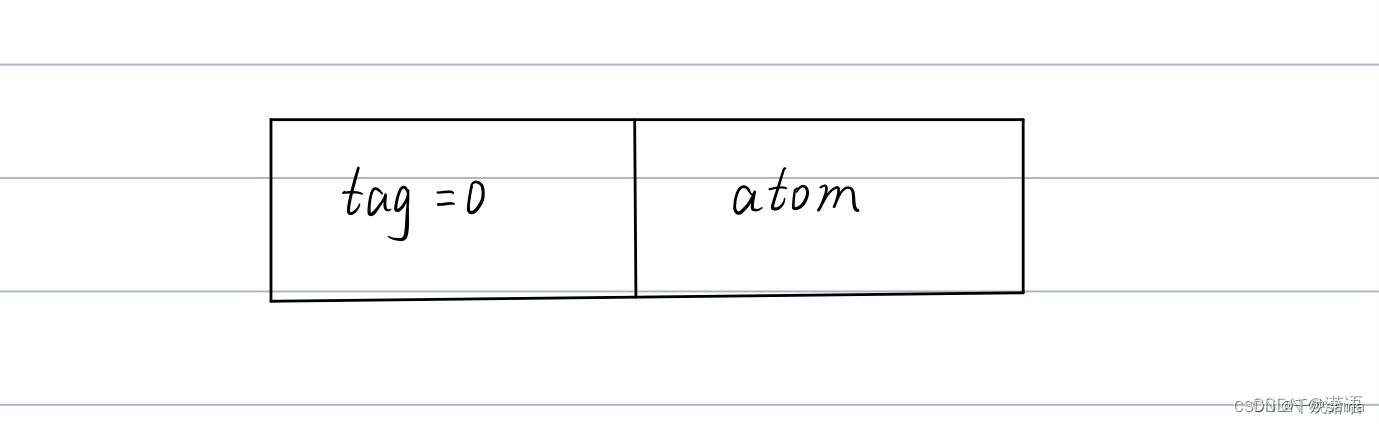
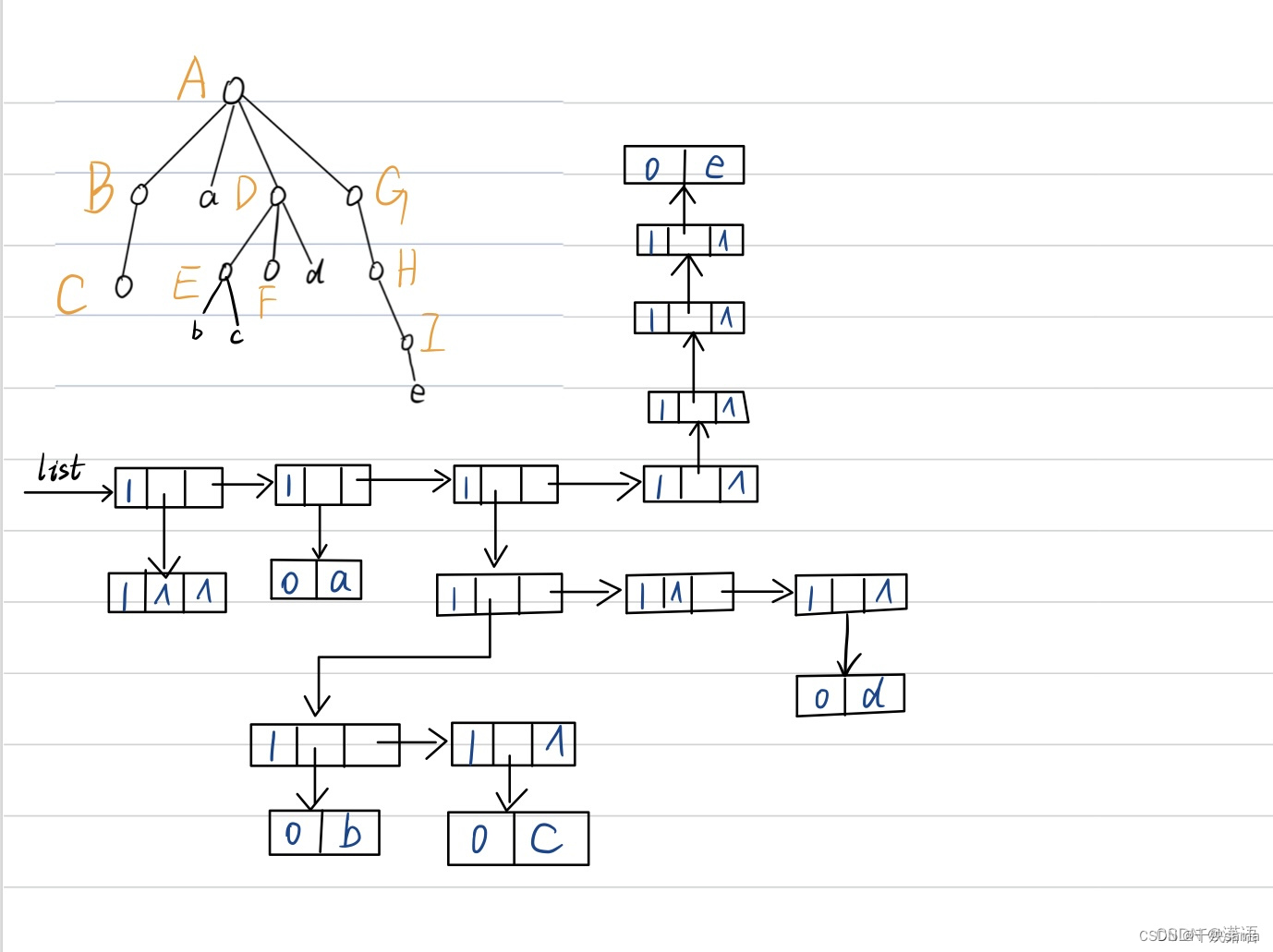
他画的这个图就比较好理解了。每个结点都有一个原子结点，原子结点的前指针hp指向原子结点的表头元素，tp指向下一个结点。

这书上的代码部分就不贴了，找了一篇比较好理解的代码实现（C）
广义表的C实现