该博客是基于清华大学出版社相关书籍的数据结构学习笔记。详细介绍了二叉树的定义、性质、存储表示、遍历方法及应用，还涉及线索二叉树、树与森林的表示和遍历、堆以及哈夫曼树的相关知识，包含概念讲解与代码实现示例。
1. 前言
本系列笔记基于 清华大学出版社的《数据结构：用面向对象方法与C++语言描述》第二版进行学习。
2. 概念
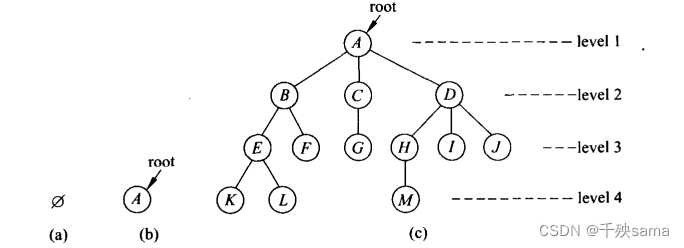
结点：包含数据项和指向其他结点的分支。
结点的度：结点所有的子树棵树。图中，A的度是3，E的度是2，K的度是0。
叶结点：度为0的结点，如K、L。
分支结点：初叶结点的其他结点。
子女结点：如果结点x有子树，结点A有3个子结点，B有两个子节点。
父结点：若x有子女，他是子女结点的父节点。
兄弟结点：同一个父结点的结点。
结点层次：结点到根结点所经路径的分支条数。
树的深度：树中离根结点最远的结点的层次。
树的度：最大的结点的度。
3. 二叉树
3.1 二叉树定义
二叉树的特点是每个结点最多有两个子女，二叉树不存在度大于2的结点，并且二叉树的子结点有左右之分，其子树的次序不能颠倒。
3.1.1 二叉树性质
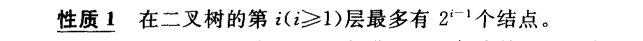
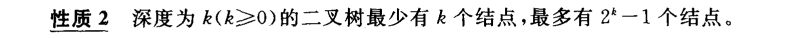
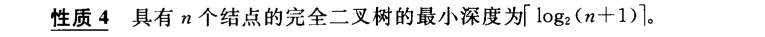
3.1.2 完全二叉树和满二叉树
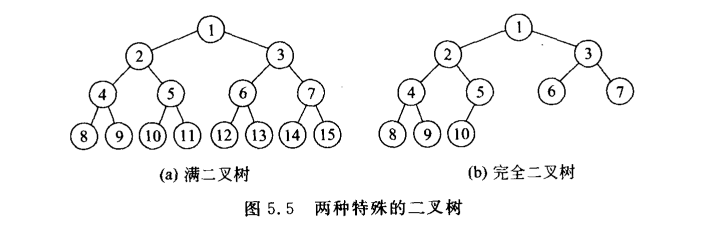
满二叉树：在满二叉树中，每一层的所有结点都达到了最大个数。
完全二叉树：除了最底层结点的度为0外，其他结点的度都为2。
（满二叉树也是完全二叉树）
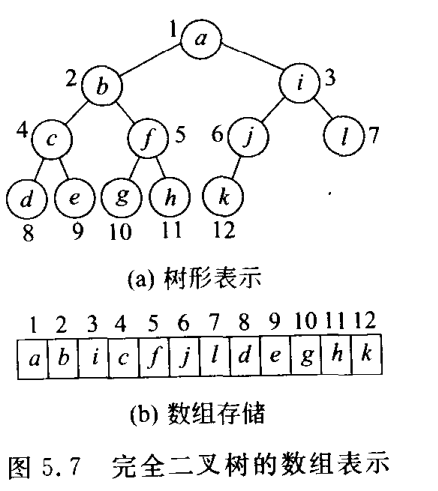
3.1.3 二叉树的数组存储表示
所有结点按层次自上而下，同一层从左到右顺序
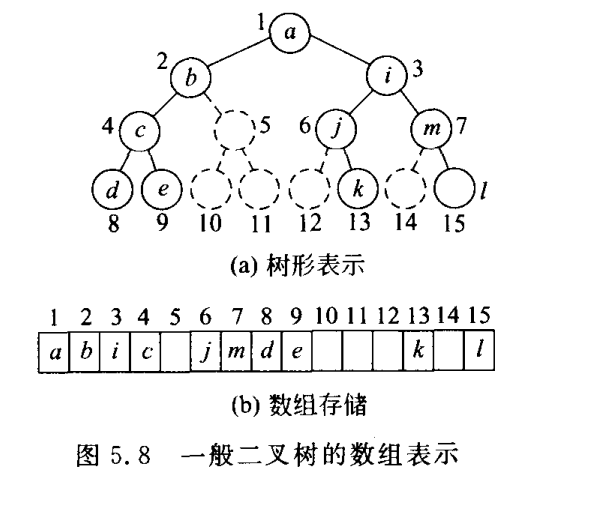
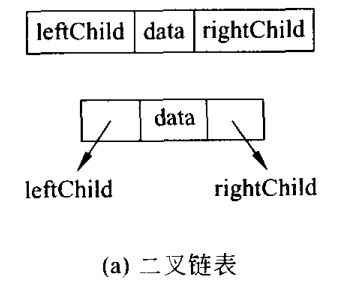
3.1.4 二叉树的链表存储表示
结点至少应该包括三个域，左子结点（leftChild指针）和右结点（rightChild指针），使用这种结构可以方便的找到子女结点，但缺点是很难找到父结点。
可以在结点中再增加一个父结点指针域，指向其父结点。如
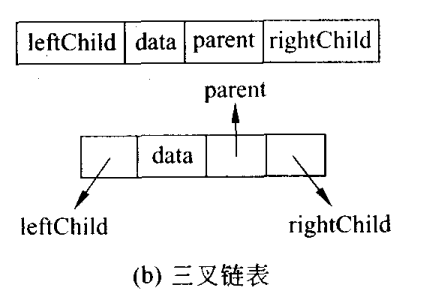
按上述方法存储，
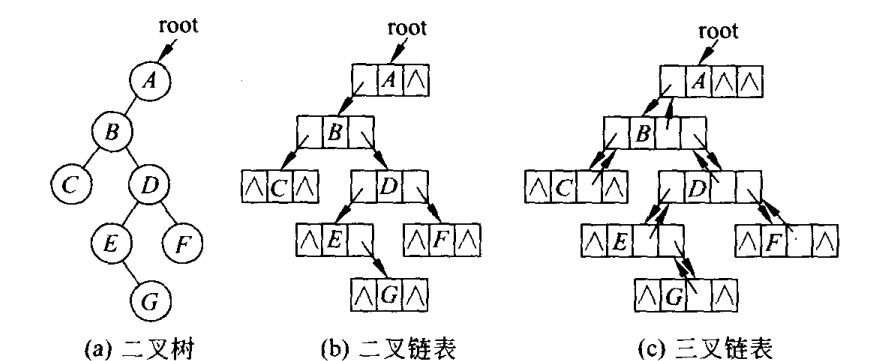
3.1.5 采用广义表建立二叉树
1）表中如果是字母，则表示是结点的值，把结点作为一个新的结点，并把结点的左子结点或右子结点连接到父结点上。
2）若是左括号，则表示子表的开始，若是右括号，则表示子表的结束。
3）使用逗号分隔左子结点和右子结点。
代码实现：
void BinaryTree::CreateBinTree(istream& in, BinTreeNode* subTree)
{
Stack<BinTreeNode*> s; // 建立栈
subTree = NULL; // 置空二叉树
BinTreeNode* p, * t, int k; // 用k作为处理左、右子树标记
char ch;
in >> ch; // 读取
while (ch != RefValue) { // 读取到非终结字符串
switch (ch) {
case '(' :
s.Push(p);
k = 1; break; // 进入子树
case ')':
s.Pop(t);
break;
case ',':
k = 2; break;
default:p = new BinTreeNode(ch);
if (subTree == NULL) subTree = p; // 如果是空树，则建立新树
else if (k == 1) {
s.getTop(t);
t->leftChild = p;
}
else {
s.getTop(t);
t->rightChild = p; //
}
}
in >> ch;
}
}
直接看代码有点难以理解，我使用书上的A(B(D,E(G,)),C(,F))# 作为例子一步一步讲解，建议画个图按下面的步骤进行理解。
1）读取字符 A。 由于是空树，以A作为根节点创建新树。
2）读取字符 （。将刚创建的A存入栈中，作为下结点的父结点备用，并将K=1，表示下一个结点如果是普通字符则为左子节点。此时栈从栈顶到栈尾为A
3）读取字符 B。K=1，作为子结点，先读取栈顶的字符A，将B作为A的左子结点存储。
4）读取字符 （。将B存入栈中，并将K=1。此时栈从栈顶到栈尾为B A。
5) 读取字符D。由于K=1，则取栈顶字符B，将D作为左子结点。
6）读取字符，。将K=2，表明接下来的字符可能是右子结点。
7）读取字符E。由于K=2，取栈顶字符B，将E作为B的右子结点。
8）读取字符（。将刚创建的E存入栈顶，并将K=1。此时栈从栈顶到栈尾 E,B,A
9）读取字符 G。K=1，将G作为E的左子结点存储。
10）读取字符，。将K=2。
11）读取字符），将栈顶元素E出栈，表明该结点已无子结点，此时栈从栈顶到栈尾为B，A
12）读取字符），将栈顶元素B出栈，此时栈只有根结点A
13）读取字符，将K=2，表明将存储可能出现的栈顶结点A的右子结点。
14）读取字符C，取栈顶元素A，K=2，将C作为A的右子结点存储
15）读取字符（，将刚创建的结点C作为新的父结点存储到栈内，此时栈从栈顶到栈尾为C A
16）读取字符，。将K=2。
17）读取字符F，取栈顶元素C，K=2，将F作为C的右子结点存储。
18） 读取字符），将栈顶元素C出栈
19）读取字符），将栈顶元素A出栈，
20）读取字符#，结束树。
最后得到的树:
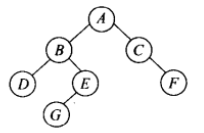
3.1.6 二叉树的遍历
二叉树右三种遍历方法，分别是前序遍历，中序遍历和后序遍历。
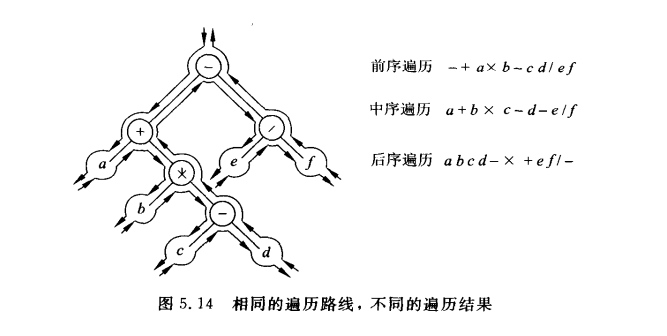
VLR（前序遍历），LVR（中序遍历），LRV（后序遍历）
三个函数中visit函数位置不一样，
有篇博文介绍了*visit 函数指针
函数指针的作用：*visit函数
实现
void BinaryTree::preOrder(BinTreeNode* subTree, void(*visit)(BinTreeNode* p)) // 前序遍历
{
if (subTree != NULL) {
visit(subTree);
preOrder(subTree->leftChild, visit); // 前序遍历左子树
preOrder(subTree->rightChild, visit); // 前序遍历右子树
}
};
void BinaryTree::InOrder(BinTreeNode* subTree, void(*visit)(BinTreeNode* p))
{
if (subTree != NULL) {
InOrder(subTree->leftChild, visit);
visit(subTree);
InOrder(subTree->rightChild, visit);
}
};
void BinaryTree::postOrder(BinTreeNode* subTree, void(*visit)(BinTreeNode* p))
{
if (subTree != NULL) {
postOrder(subTree->leftChild, visit);
postOrder(subTree->rightChild, visit);
visit(subTree);
}
};
关于三种遍历的理解，找到篇博客
数据结构——二叉树先序、中序、后序及层次四种遍历（C语言版）
3.1.7 二叉树的遍历的应用
1.后序遍历的应用
int BinaryTree::Height(BinTreeNode* subTree)
{
if (subTree == NULL) return 0;
else {
int i = Height(subTree->leftChild);
int j = Height(subTree->rightChild);
return (i < j) ? j + 1 : i + 1;
}
}
int BinaryTree::Size(BinTreeNode* subTree) // 后序遍历计算结点个数
{
if (subTree == NULL) return 0;
else return 1 + Size(subTree->leftChild) + Size(subTree->rightChild);
}
2.前序遍历的应用
树的复制
BinaryTree::BinaryTree(BinaryTree& s)
{
root = Copy(s.root);
}
BinTreeNode* BinaryTree::Copy(BinTreeNode* orignode)
{
if (orignode == NULL) return NULL;
BinTreeNode* temp = new BinTreeNode;
temp->data = orignode ->data;
temp->leftChild = Copy(orignode->leftChild);
temp->rightChild = Copy(orignode->rightChild);
return temp;
}
判断树是否相同
bool BinaryTree::Equal(BinTreeNode* a, BinTreeNode* b)
{
if (a == NULL && b == NULL) return true;
if (a != NULL && b != NULL && a->data == b->data
&& Equal(a->leftChild, b->leftChild)
&& Equal(a->rightChild, b->rightChild)
)
return true;
else return false;
}
创建新树
void BinaryTree::CreateBinTree(istream& in, BinTreeNode* subTree)
{
int item;
if (!in.eof()) {
in >> item;
if (item != RefValue) {
subTree = new BinTreeNode(item);
if (subTree == NULL) {
cout << "error when allocate memory!" << endl;
}
CreateBinTree(in, subTree->leftChild);
CreateBinTree(in, subTree->rightChild);
}
else subTree = NULL;
}
}
输出二叉树，使用广义表进行输出
void BinaryTree::PrintBTree(BinTreeNode* BT) {
if (BT != NULL) {
cout << BT->data;
if (BT->leftChild != NULL || BT->rightChild != NULL) {
cout << "(";
PrintBTree(BT->leftChild);
cout << ",";
if (BT->rightChild != NULL)
PrintBTree(BT->rightChild);
cout << ")";
}
}
}
3.1.7 二叉树的非递归算法
3.1.7.1 利用栈的前序遍历非递归算法
/*前序遍历非递归！ 方法1*/
void BinaryTree::preOrder(void(*visit)(BinTreeNode* p)) // 前序遍历
{
stack S;
BinTreeNode* p = root;
S.Push(NULL);
while (p != NULL) {
visit(p);
if (p->rightChild != NULL) S.Push(p->rightChild);
if (p->leftChild != NULL) p = p->leftChild;
else S.Pop(p);
}
};
/*前序遍历非递归！ 方法2*/
void BinaryTree::preOrder(void(*visit)(BinTreeNode* p)) {
stack S;
BinTreeNode* p;
s.Push(root);
while (!S.isEmpty()) {
S.Pop(p); visit(p);
if (p->rightChild != NULL) S.Push(p->rightChild);
if (p->leftChild != NULL) S.Push(p->leftChild);
}
}
3.1.7.2 利用栈的层次遍历非递归算法
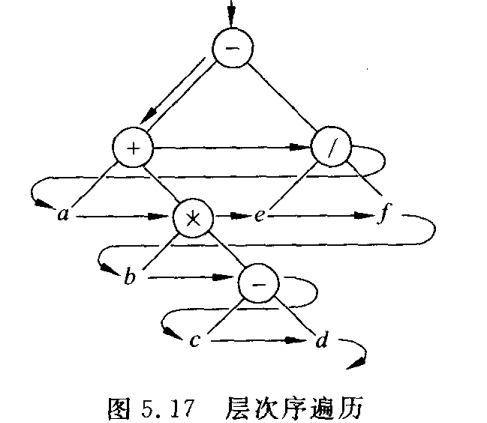
void BinaryTree::LevelOrder(void(*visit)(BinTreeNode* p)) {
Queue Q;
BinTreeNode* p = root;
Q.EnQueue(p);
while (!Q.IsEmpty()) {
Q.DeQueue(p); visit(p);
if (p->leftChild != NULL) Q.EnQueue(p->leftChild);
if (p->rightChild != NULL) Q.EnQueue(p->rightChild);
}
}
3.1.7.3 利用栈的中序遍历非递归算法
void BinaryTree::InOrder(void(*visit)(BinTreeNode* p)) {
Stack S;
BinTreeNode* p = root;
do {
while (p != NULL) {
S.Push(p);
p = p->leftChild
}
if (!S.IsEmpty()) {
S.Pop(p);
visit(p);
p = p->rightChild;
}
} while (p!=NULL || !S.IsEmpty());
}
3.1.7.4 利用栈的后序遍历非递归算法
void BinaryTree::postOrder(void(*visit)(BinTreeNode* p)) {
Stack S;
stkNode w;
BinTreeNode* p = root;
do {
while (p != NULL) {
w.ptr = p;
w.tag = L;
S.Push(w);
p = p->leftChild;
}
int continue1 = 1;
while (continue1 && !S.IsEmpty()) {
S.Pop(w);
p = w.ptr;
switch (w.tag) {
case L:
w.tag = R;
S.Push(w);
continue1 = 0;
p = p->rightChild;
break;
case R:
visit(p);
break;
}
}
}while (!S.IsEmpty());
cout << endl;
}
3.1.7.5 树的计数
书上写得代码真的很难想，使用javascrip的代码很好理解
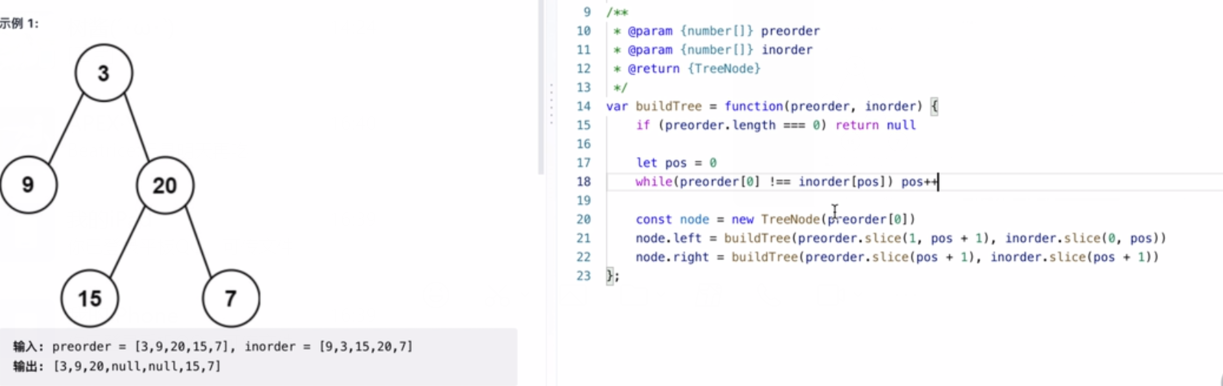
4.线索二叉树
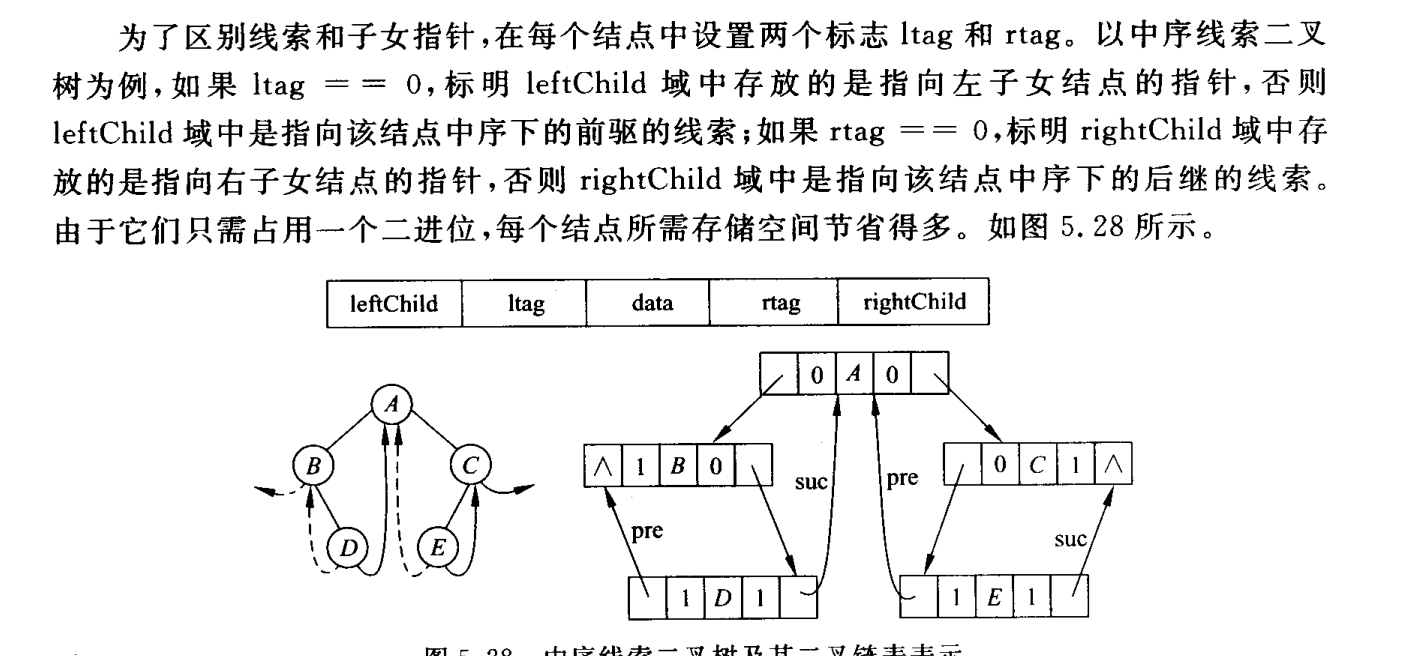
前驱是什么呢，比如说前序遍历：DBEACF
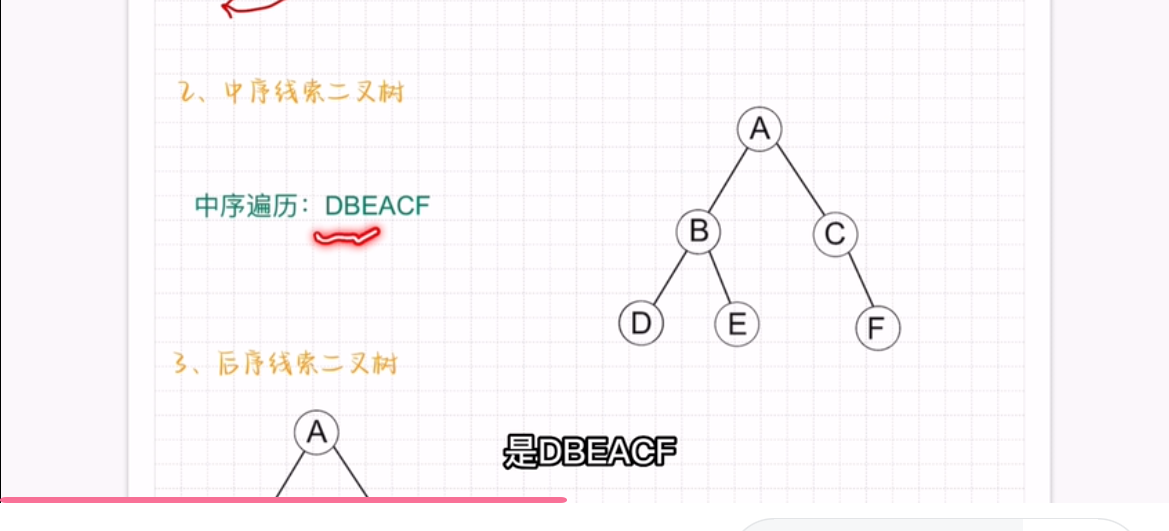
C是没有左子结点的，所以指向他的leftChild指向前驱是A结点，ltag = 1，rightChild指向F，rtag == 0。
D、E、F没有左右子结点，D结点没有前驱，leftChild指向NULL，rightChild指向b。E结点leftChild指向前驱B，rightChild 指向后驱A，F的leftChild指向前驱C，rightChild指向后驱NULL。
简单来说，如果需要找到指定结点的后继结点，如果在rtag中，rtag == 1，则表明有后继线索，rightChild中存放的是直接后继。如果rtag==0，则表示没有后继线索，存放的是右子女的指针，需要通过一定运算才能找到他的后继。
如果要找到指定结点的前驱结点，如果在ltag中，ltag == 1，则表示右前驱线索，leftChild中存放的是直接前驱。如果ltag==0，则表示没有前驱线索，存放的是做子女结点。
4.1 中序线索二叉树的遍历
void ThreadTree::Inorder(void(*visit)(ThreadNode* p))
{
ThreadNode* p;
for (p = First(root); p != NULL; p = Next(p)) visit(p);
}
ThreadNode* ThreadTree::First(ThreadNode* current)
{
ThreadNode* p = current;
while (p->ltag == 0) p = p->leftChild;
return p;
}
ThreadNode* ThreadTree::Next(ThreadNode* current)
{
// rtag == 0
ThreadNode* p = current->rightChild;
if (current->rtag == 0) // 没有右驱线索
return First(p);
else return p;
}
4.2 中序线索二叉树的线索化
B站上有一个视频，讲的很好
二叉树的中序线索化思路&代码分享| 我愿称为你逃我追法！
在书中的代码体现就是Current先行，然后Pre再后行，current先行的指针先解决ltag和leftchild，Pre后行的指针会沿着p走的路解决rtag和rightChild。
void ThreadTree::createInThread(ThreadNode* current, ThreadNode*& pre)
{
// pre 处理好的
// p
if (current == NULL) return;
createInThread(current->leftChild, pre); // 递归左孩子
if (current->leftChild == NULL)
{
current->leftChild = pre;
current->ltag = 1;
}
if (pre != NULL && pre->rightChild == NULL) // 递归右孩子
{
pre->rightChild = current;
pre->rtag = 1;
}
pre = current; // 把current赋给pre，标记当前结点成为新的前驱结点
createInThread(current->rightChild, pre);
}
void ThreadTree::createInThread()
{
ThreadNode* pre = NULL;
if (root != NULL) {
createInThread(root, pre); // 递归树
pre->rightChild = NULL;
pre->rtag = 1;
}
}
4.3 在线索二叉树上实现前序遍历的算法
void ThreadTree::PreOrder(void(*visit)(ThreadNode* p))
{
ThreadNode* p = root;
while (p != NULL) {
visit(p);
if (p->ltag == 0) p = p->leftChild; // 有左子女，即为后继
else if (p->rtag == 0) p = p->rightChild; // 否则有右子子女，为后继
else {
while (p!=NULL && p->rtag == 1) // 延后继线索检测
{
p = p->rightChild; // 直到有右子女结点
if (p != NULL) p = p->rightChild; // 右子女即为后继
}
}
}
}
4.4 在线索二叉树上实现后续遍历的算法
void ThreadTree::PostOrder(void(*visit)(ThreadNode* p))
{
ThreadNode* t = root;
while (t->ltag == 0 || t->rtag == 0)
if (t->ltag == 0) t = t->leftChild;
else if (t->rtag == 0) t=t->rightChild;
visit(t);
ThreadNode* p;
while ((p = parent(t)) != NULL) {
if (p->rightChild == t || p->rtag == 1)
t = p;
else {
t = p->rightChild;
while (t->ltag == 0 || t->rtag == 0)
if (t->ltag == 0) t = t->leftChild;
else if (t->rtag == 0) t = t->rightChild;
}
visit(t);
}
}
4.5 在线索二叉树上寻找父结点
ThreadNode* ThreadTree::parent(ThreadNode* t)
{
ThreadNode* p;
if (t == root) return NULL; // 根节点无父结点
for (p = t; p->ltag == 0; p = p->leftChild); // 求*t为根子树的第一个结点
if (p->leftChild != NULL)
for (p = p->leftChild; p != NULL && p->leftChild != t && p->rightChild != t; p = p->rightChild);
if (p == NULL || p->leftChild == NULL) {
for (p = t; p->rtag == 0; p = p->rightChild);
for (p = p->rightChild; p != NULL && p->leftChild != t && p->rightChild != t; p = p->leftChild);
}
return p;
}
5.树与森林
对于一般的树，由于每个结点的分支数可能不等，其存储表示有多种。
5.1 树的表示
5.1.1 广义表表示
广义表的表示已经在前面（3.1.5）说明过了，忘了可以跳回去看。
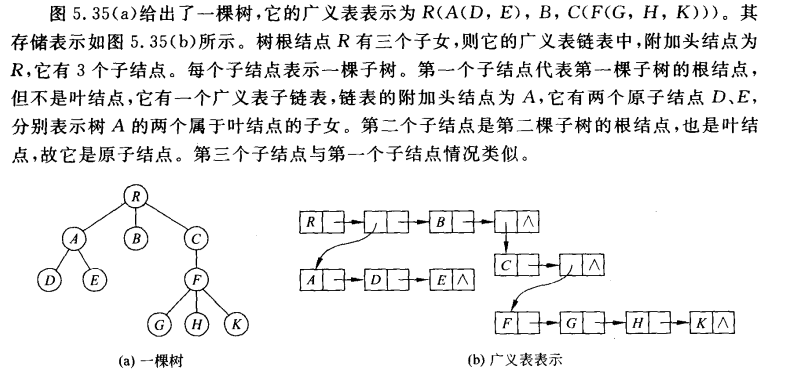
5.1.2 父指针表示
用一组连续的存储单元存放树中的结点。这种存储方式也在上面介绍过。
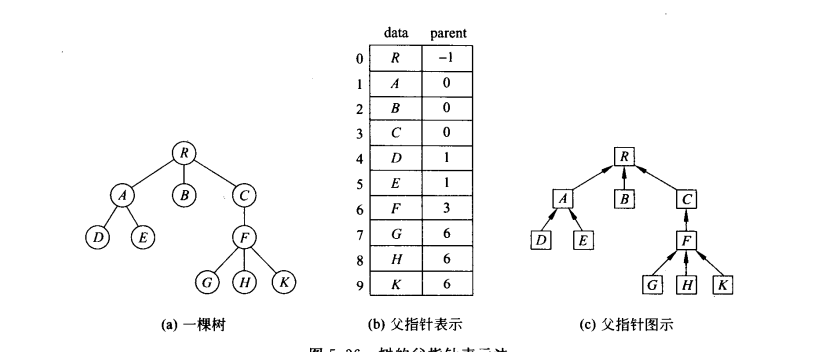
5.1.3 子女链表表示
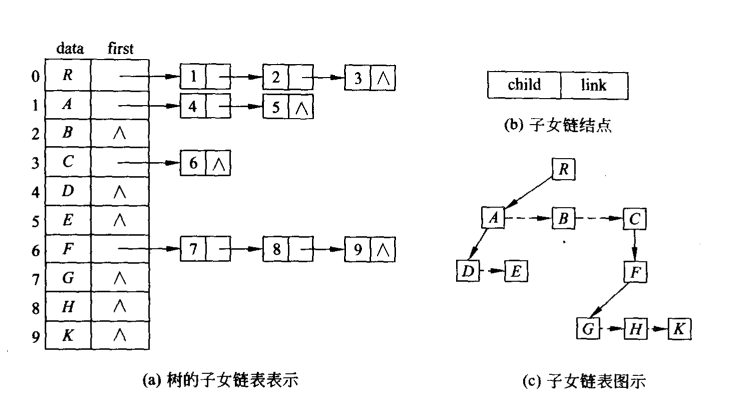
5.1.4 子女-兄弟链表表示
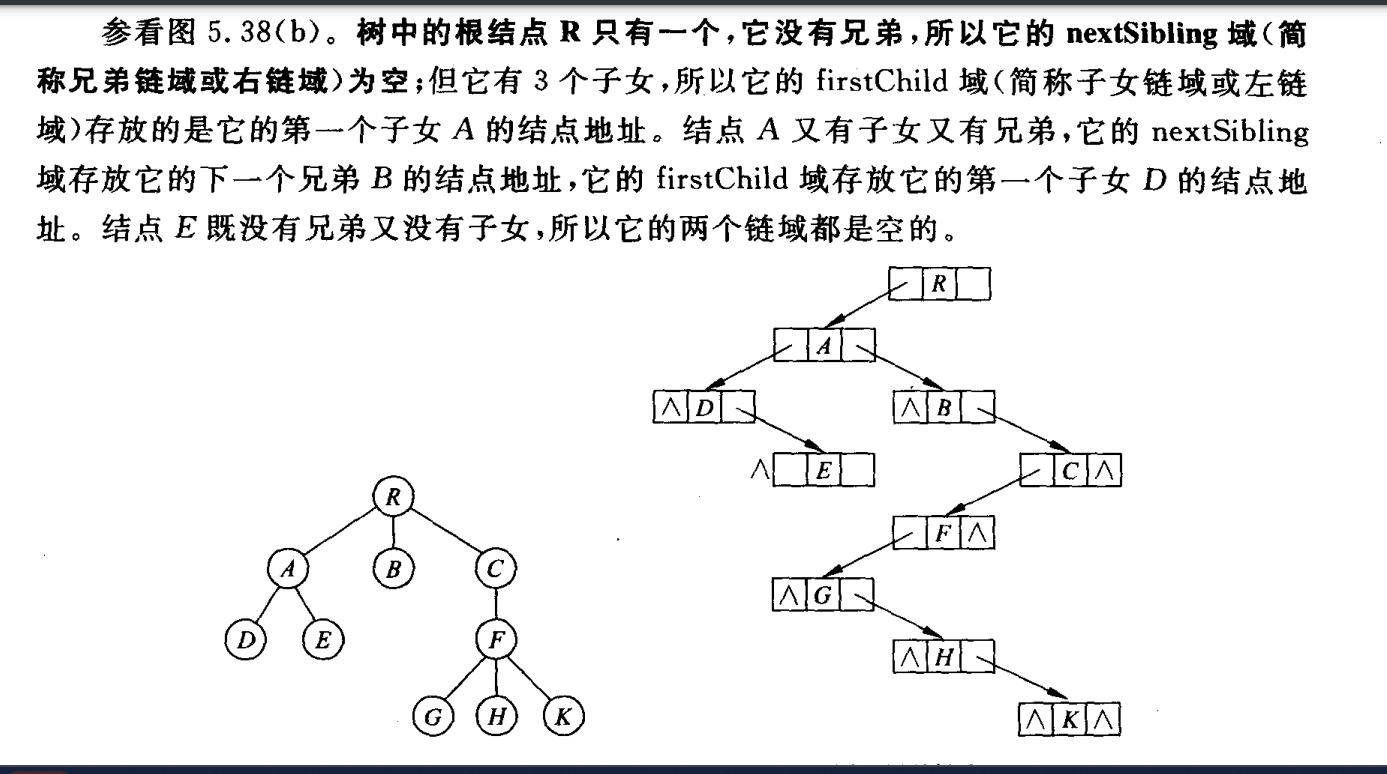
如果要访问A的所有子女结点，先通过A的firstChild指针找到D,再通过他的nextSibling指针找到下一个兄弟E，E的nextSibling指针为空，所以检测结束。这种存储方式是通过二叉链表结构的表示。
5.2 子女-兄弟链表部分实现
#include <iostream>
struct TreeNode {
int data;
TreeNode* firstChild, * nextSibling; // 子女及兄弟指针
TreeNode(int value = 0, TreeNode* fc = NULL, TreeNode* ns = NULL)
: data(value), firstChild(fc), nextSibling(ns) {}
};
class Tree {
public:
Tree() { root = NULL; current = NULL; }
bool Root(); // 寻找根
bool IsEmpty() { return root == NULL; } // 判空树
bool FirstChild(); // 寻找当前结点的第一个子女，使之成为当前结点
bool NextSibling(); // 寻找下一个兄弟结点
bool Parent();
bool Find(int target);
private:
TreeNode* root, * current;
bool Find(TreeNode* p, int value); // 在以P为根的树中搜索value
void RemovesubTree(TreeNode* p); // 删除以p为根的子树
bool FindParent(TreeNode* t, TreeNode* p);
};
int main()
{
std::cout << "Hello World!\n";
}
bool Tree::Root()
{
if (root == NULL)
{
current = NULL;
return false;
}
else
{
current = root;
return true;
}
}
bool Tree::FirstChild()
{
if (current != NULL && current->firstChild != NULL) {
current = current->firstChild;
return true;
}
current = NULL;
return false;
}
bool Tree::NextSibling()
{
if (current != NULL && current->nextSibling != NULL) {
current = current->nextSibling;
return true;
}
current = NULL;
return false;
}
bool Tree::Parent()
{
TreeNode* p = current;
if(current==NULL || current==root)
{
current = NULL;
return false;
}
return FindParent(root, p);
}
bool Tree::Find(int target)
{
if (IsEmpty()) return false;
return Find(root,target);
}
bool Tree::Find(TreeNode* p, int value)
{
// 在根为*p的树中找值为value的结点，找到后该节点成为当前结点
bool result = false;
if (p->data == value) { result = true; current = p;}
else {
TreeNode* q = p->firstChild;
while (q != NULL && !(result = Find(q, value))) {
q = q->nextSibling;
}
}
return result;
}
bool Tree::FindParent(TreeNode* t, TreeNode* p)
{
TreeNode* q = t->firstChild;
bool succ;
while (q!=NULL&&q!=p) // 搜索长子的兄弟链
{
if ((succ = FindParent(q, p)) == true) return succ; // 以新的结点作为树根递归
q = q->nextSibling; // 如果不是子女，就往兄弟方向靠
}
if (q != NULL && q == p) // 找到，并付给current指针
{
current = t;
return true;
}
else { current = NULL; return false; } // 未找到父结点
}
5.3 森林与二叉树的转换
书上讲的有点难懂，但其实把子女-兄弟树理解了就很好明白了。如图。
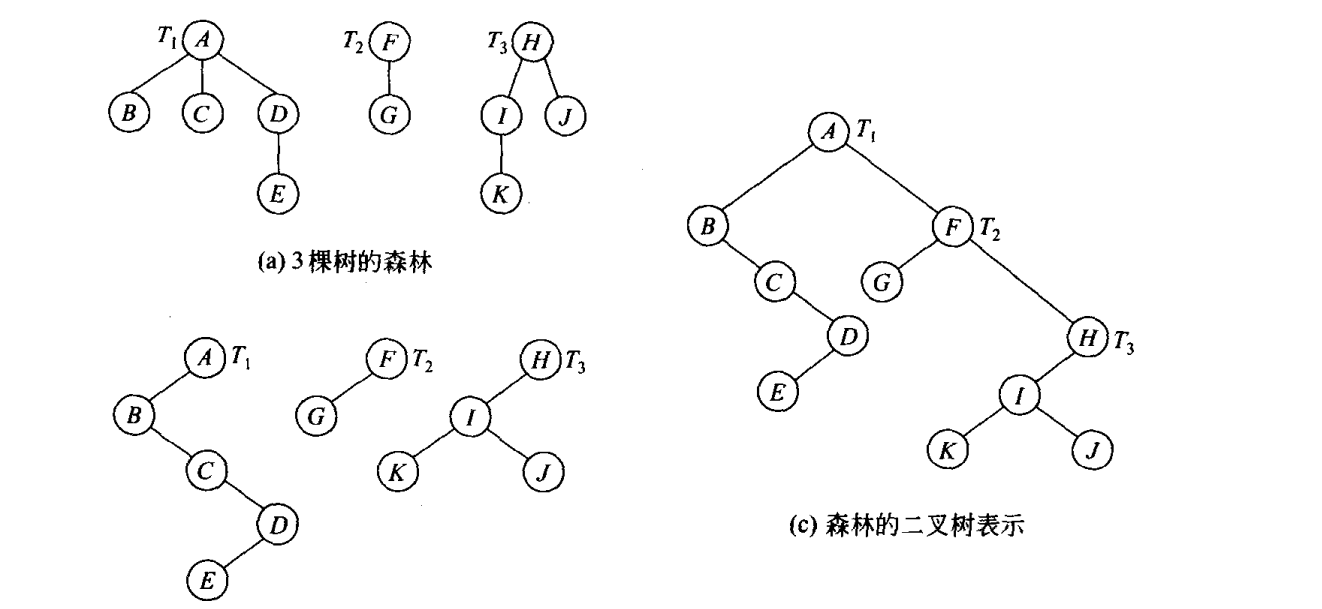
5.4 树和森林的遍历
5.4.1 树的深度优先遍历
1）先根次序遍历
①访问树的根节点r；
②依次先根次序遍历根的各子树
2）后根次序遍历
①依次后根次序遍历根的各子树
②访问树的根节点
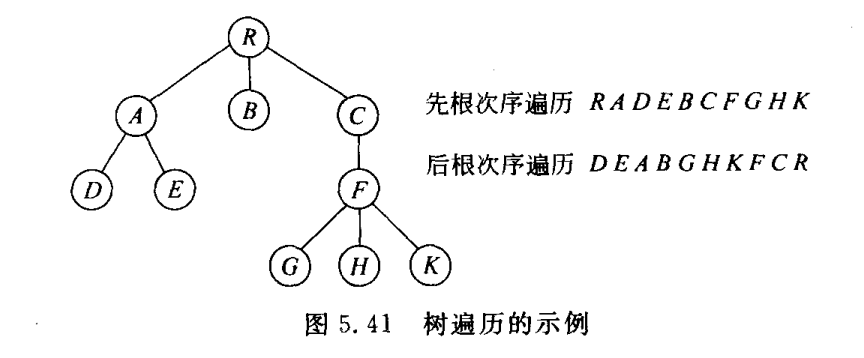
5.4.2 森林的深度优先遍历
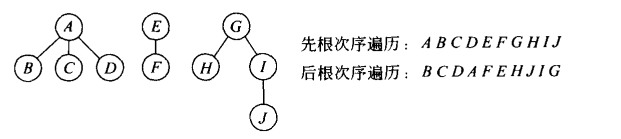
可以借助二叉树实现树的先根遍历和和后根遍历
如何转换在上面介绍过了
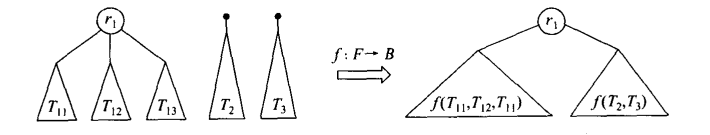
相当于把leftchild换成了firstchild，rightchild换成了nextSibling。
5.4.3 树的广度优先遍历
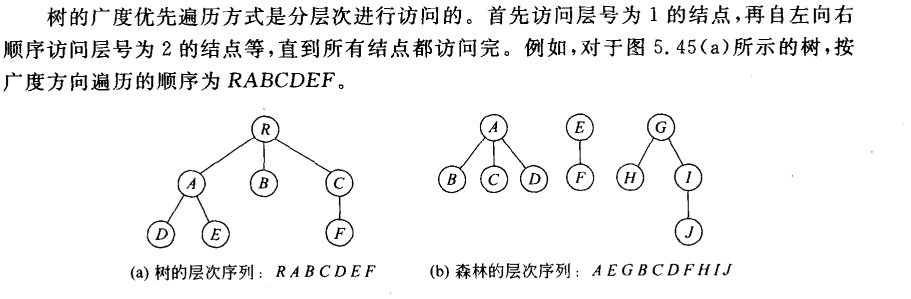
广度优先算法不是递归算法。需要借助一个队列进行分层的访问。
void Tree::LevelOrder(ostream& out, TreeNode* p)
{
Queue* Q;
if (p != NULL) {
Q.EnQueue(p); // 存根节点进队列
while (!Q.IsEmpty()) {
Q.DeQueue(p); // 出队，并把他的孩子结点和孩子节点的兄弟结点存入队列
out << p->data;
for (p = p->firstChild; p != NULL; p = p->nextSibling) // 这一结点所有兄弟结点进队
Q.EnQueue(p);
}
}
}
6.堆
6.1 最大堆和最小堆
用树存储带有关键码。如最小堆，他的关键码是集合中最小的，结点的关键码均小于或等于他的左右子女的关键码，最大堆相反。
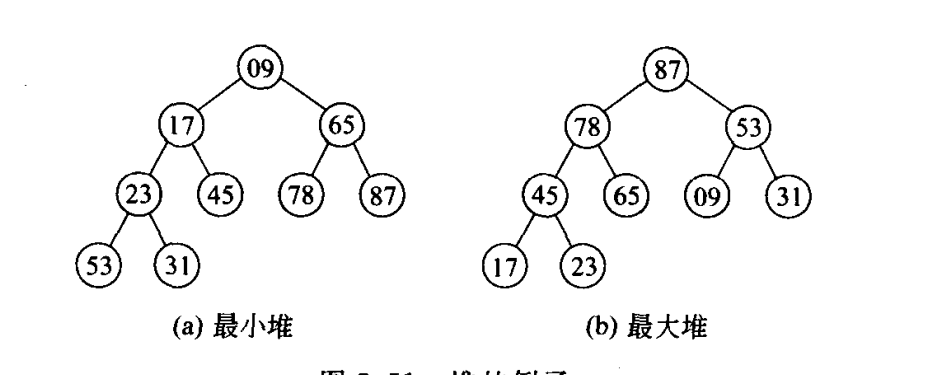
6.2 堆的建立
堆的建立首先是依次放数据使其成为二叉树，然后从 （currentSize-2）/2开始调整数据使其成为一个最小堆。
采用自下向上逐步调整行程堆的方法。
如数组 53 17 78 09 45 65 87 23
按二叉树存储，再算出（8-2）/2 = 3，就从i=3的09处开始算
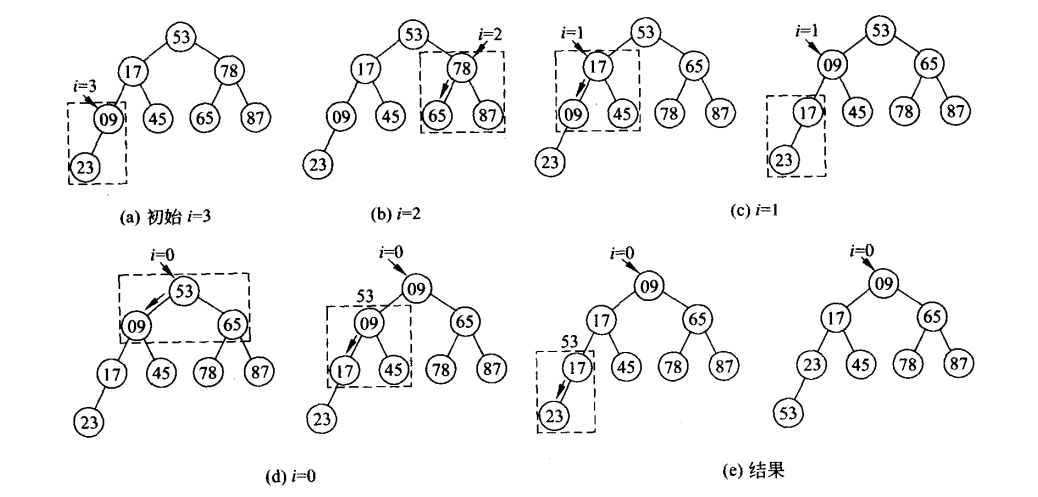
结点 i 左子女关键码小于右子女关键码，则沿左分支进行调整，否则沿右分支进行调整，用一指针 j 指向要调整的子结点。将R[i]和R[j]进行比较，如果R[i]>R[j]，则把关键码小的结点上浮。使i=j，j=2i+1；继续进行下一层的比较。如果R[i]<=r[j]，则不对调，也不向下一层继续比较，算法终止。
代码实现：
void MinHeap::siftUp(int start)
{
// 从结点start开始到结点0为止，自下向上进行比较，
// 如果子女的值小于父结点的值，则进行交换
int j = start; // 开始的地方
int i = (j - 1) / 2; // 开始的结点的父结点
int temp = heap[j]; // 暂时存放开始的结点
while (j > 0) {
if (heap[i] < temp) break; // 父结点值小，不调整
else {
heap[j] = heap[i]; // 父结点值大，交换
j = i;
i = (i - 1) / 2;
}
}
heap[j] = temp;
}
给出自上向下的算法
void MinHeap::siftDown(int start, int m)
{
// 从 start到m为止，自上向下比较，如果子女的值小于父结点的值
// 则关键码小的上浮，继续向下层比较
int i = start;
int j = 2 * i + 1; // 左子女
int temp = heap[i];
while (j <= m) {
if (j<m && heap[j]>heap[j + 1])j++; // j指向左右子女中较小的一个
if (temp <= heap[j]) break; // 如果比左子女或者右子女小，则跳出循环
else {
heap[i] = heap[j];
i = j;
j = 2 * j + 1; // 往下进行
}
}
heap[i] = temp; // 回收暂存的元素
}
很好理解
6.3 堆的插入和删除
6.3.1 插入
直接看代码
bool MinHeap::Insert(const int& x)
{
if (currentSize == maxHeapSize) {
cout << "Heap Full" << endl;
return false;
}
heap[currentSize] = x; // 存新数据
siftUp(currentSize); // 向上调整成新最小堆
currentSize++;
return true;
}
6.3.2 删除
通常来说，删除是删除堆顶的元素，给出代码很好理解。
bool MinHeap::RemoveMin(int& x)
{
// 删除堆顶元素
if (!currentSize) { cout << "heap empty" << endl; return false; } // 堆空
x = heap[0];
heap[0] = heap[currentSize - 1]; // 更改堆顶为堆中最后一个元素
currentSize--; // 删除堆中最后一个元素
siftDown(0, currentSize - 1); // 自上向下重新建堆
return true;
}
7. 哈夫曼(Huffman)树
哈夫曼树，又称最优二叉树，是一类加权路径长度最短的二叉树。
在给出哈夫曼树之前，先给出两个定义。
路径：从树的一个结点到树的另一个结点之间的分支构成改两点之间的路径。（就是线有多少条）
路径长度：路径上的分支条数。树的路径长度是从树的根节点到每个结点的路径之和。（就是根节点到每个结点有多少条线依次加起来）
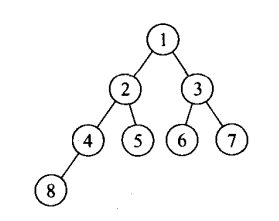
1到2的路径是1，1到5的路径是2，1到8的路径是3。二叉树的路径长度就是0+1+1+2+2+2+2+3=13
7.1 哈夫曼树
给每个叶结点付给各自的权值，记住是叶节点。
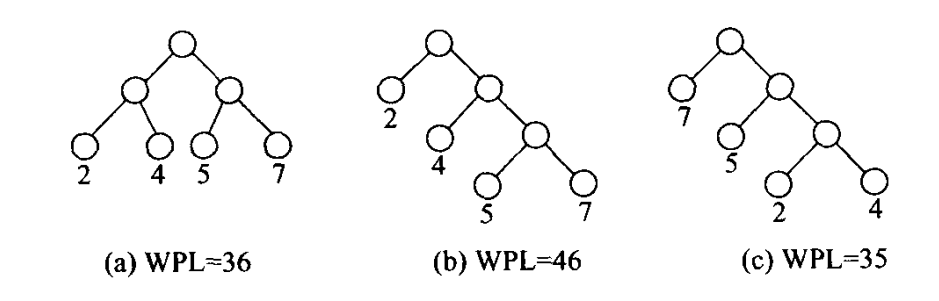
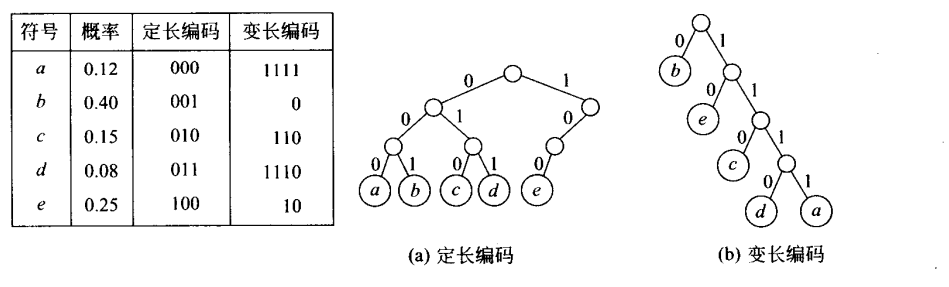
图a的二叉树的权值，权值为2的叶节点：到根节点两条线2 乘自身权值 即22=4，权值为4的叶节点：到根节点2乘自身权值24=8.
所以WPL=22+42+52+72。
图b的二叉树，权值为2的叶节点，到根节点1根线，21=2。权值为5的叶节点，到根节点3条线 35=15.
WPL=21+42+53+73=46。
图c同理，WPL=71+52+23+43=35。
带权路径最下的二叉树应该是权值大的外结点离根结点最近的扩充二叉树。就叫哈夫曼（huffman）树。
7.2 建立哈夫曼树
1）首先根据权值，构造具有扩充二叉树的森林，即每个结点都成为森林的一棵树，但没有子女节点的树。
重复以下步骤，知道F中只剩下一棵树
2）在森林中选择两颗根节点权值最小的扩充二叉树，作为左右子树构造一棵新的二叉树。新的二叉树根结点权值为左右子树根结点的权值之和，即刚选的两根结点权值之和。
3）在F中删掉刚选择的两颗树
4）把新的二叉树加入F，即让他们的权值加入F中
例如 {7，5，2，4}构造huffman树。
1）根据权值创建F即
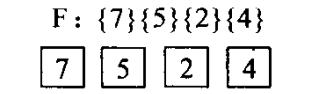
2）选择最小的两个权值即2，4，组成新的树，删除F中的2，4，将其权值2+4=6加入F
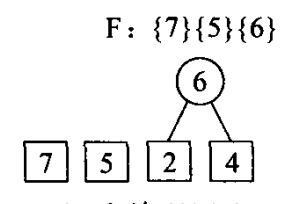
3）选择权值最小的两颗树5，6，组成新的树，将新树5+6=11.存入F，删除老树5、6.
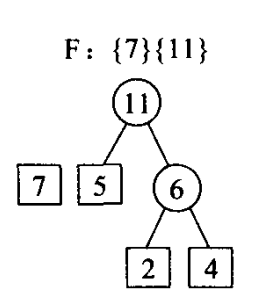
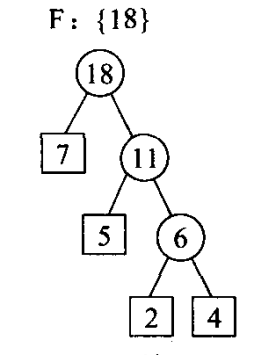
4）选择最小的两棵树7、11组成新树，将老树7、11删除，插入新树11+7=18，由于只有一颗树了，所以即为huffman树
void HuffmanTree::mergeTree(HuffmanNode& ht1, HuffmanNode& ht2, HuffmanNode*& parent)
{
parent = new HuffmanNode();
parent->leftChild = &ht1;
parent->rightChild = &ht2;
parent->data = ht1.data + ht2.data;
ht1.parent = parent;
ht2.parent = parent;
}
HuffmanTree::HuffmanTree(int w[], int n)
{
// 给出n个权值w[1]~w[n]，构造哈夫曼树
MinHeap hp; // 使用最小堆存放森林
HuffmanNode* parent;
HuffmanNode& first;
HuffmanNode& second;
HuffmanNode* NodeList = new HuffmanNode[n];
for (int i = 0; i < n; i++) {
NodeList[i].data = w[i+1];
NodeList[i].leftChild = NULL;
NodeList[i].rightChild = NULL;
NodeList[i].parent = NULL;
hp.Insert(NodeList[i]); // 插入最小堆中
}
for (int i = 0; i < n - 1; i++) {
hp.RemoveMin(first);
hp.RemoveMin(second);
mergeTree(first, second, parent); // 合并成一棵树
hp.Insert(*parent); // 插入新树
root = parent; // 重新建立结点
}
}
7.2 哈夫曼编码
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
