本文详细介绍了栈、队列和递归的基本概念、顺序栈和链式栈的实现、双向栈和循环队列的定义与操作，以及递归在计算阶乘、汉诺塔等问题中的应用。
文章目录
1. 前言
本系列笔记基于 清华大学出版社的《数据结构：用面向对象方法与C++语言描述》第二版进行学习。
2. 概念
栈和队列是两种特殊的线性表，逻辑结构和线性表相同，但有更多使用上的限制，故又称为受限的线性表。
3. 栈
3.1 栈的定义
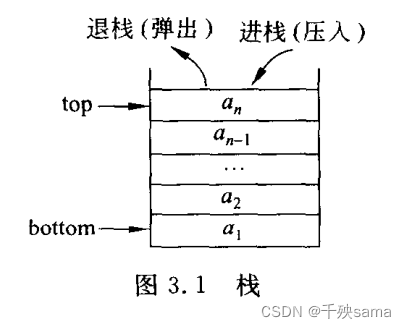
栈可定义为只允许在表的末端进行插入和删除的线性表。允许插入和删除的一端叫栈顶，不允许插入和删除的一端叫栈底。栈属于后进先出的线性表，进栈和出栈的顺序相反。
3.1.1 顺序栈定义
顺序栈是基于顺数组的存储表示实现。
3.1.2 顺序栈实现
栈的构造函数
SeqStack::SeqStack(int sz = 50) {
top = -1;
maxSize = sz;
elements = new int[maxSize];
assert(elements != NULL);
};
assert 断言，如果断言中内容不符合，则退出程序，如符合，继续执行后续语句。
3.1.3 顺序栈的进栈退栈
如图，进栈时元素进入top的位置进行存储，top上移一位（top+1），出栈时删除在top的元素，top下移一位。
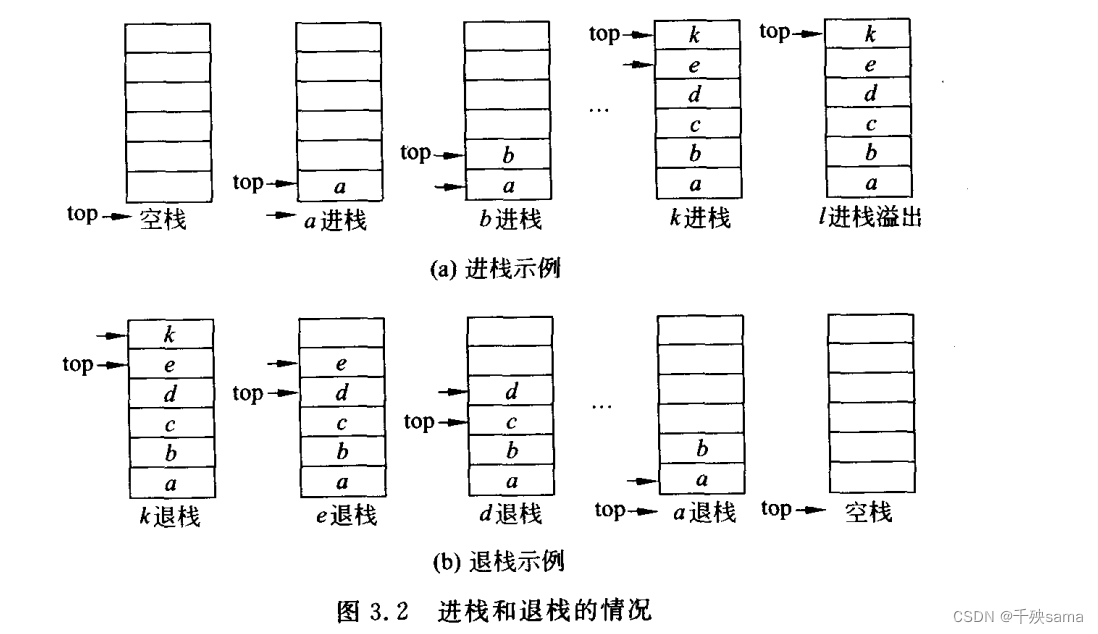
当top = maxsize - 1 时，则表示栈满，如果此时需要再入栈新元素，将进行溢出处理。
3.1.4 顺序栈的实现
#include <iostream>
#include <assert.h>
using namespace std;
const int stackIncreament = 20;
class SeqStack {
public:
SeqStack(int sz = 50); // 建立栈
~SeqStack() { delete[]elements; }
void Push(const int& x); // 插入x到栈顶
bool Pop(int &x); // 出栈顶元素
bool getTop(int& x); // 获得栈顶元素
bool IsEmpty()const { return (top == -1) ? true : false;}
bool IsFull()const { return (top == maxSize - 1) ? true : false; }
int getSize()const {return top + 1;} // 函数返回栈中元素的个数
void MakeEmpty() { top = -1; } // 清空栈的内容
private:
int* elements; // 存放栈中元素的栈数组
int top; // 栈顶标识
int maxSize; // 栈最大可容纳元素个数
void overflowProcess(); // 栈的溢出处理
};
SeqStack::SeqStack(int sz) {
top = -1;
maxSize = sz;
elements = new int[maxSize];
assert(elements != NULL);
};
void SeqStack::overflowProcess() { // 溢出操作，申请新内存
int* newArray = new int[maxSize + stackIncreament];
if (newArray == NULL) {
cout << "error when allocate memory" << endl; exit(1);
}
for (int i = 0; i <= top; i++) newArray[i] = elements[i];
maxSize = maxSize + stackIncreament;
delete[]elements;
elements = newArray;
};
void SeqStack::Push(const int& x) {
if (IsFull() == true) overflowProcess(); // 溢出处理
top++;
elements[top] = x;
};
bool SeqStack::Pop(int& x) {
if (IsEmpty() == true) return false;
x = elements[top];
top--;
return true;
};
bool SeqStack::getTop(int& x) {
if (IsEmpty() == true) return false;
x = elements[top];
return true;
};
int main()
{
}
3.2 双向栈定义
当程序同时需要两个栈时，可以定义一个空间足够的栈，让空间的两端作为两个栈的栈底，让两个栈分别向栈的空间伸展，直到两个栈顶相遇。如b[0]和b[1]分别作为两个栈的栈底，元素入栈t[0]和t[1]分别向栈中心伸展。
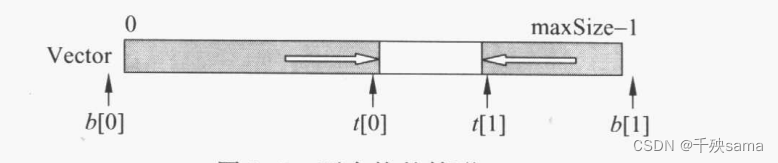
每次进栈时t[0] + 1，t[1] - 1，退栈时相反。
在双栈情形下，初始化语句 t[0] = b[0] = -1; t[1] = b[1] = maxSize，栈满时t[0]+1 == t[1]。
栈空的条件时t[0] = b[0] 或 t[1] = b[1]。
3.2.1 双向栈的插入和删除
bool push(DualStack& DS, int& x, int d) { // d=0时在0号栈插入，d=1时在1号栈插入
if (DS.t[0] + 1 == DS.t[1]) return false; // 栈满
if (d == 0) DS.t[0]++;
else DS.t[1]--;
DS.Vector[DS.t[d]] == x;
return true;
}
bool Pop(DualStack& DS, int& x, int d) {// d=0时在0号栈插退栈，d=1时在1号栈退栈
if (Ds.t[d] == DS.b[d]) return false;
x = DS.Vector[DS.t[d]];
if (d == 0) DS.t[0]--;
else DS.t[1]++;
return true;
}
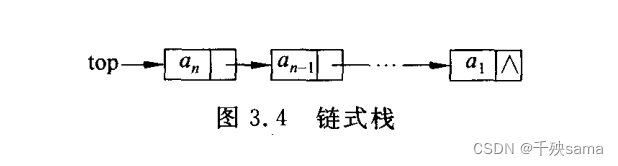
3.2.2 链式栈类定义
链式栈时栈的链接存储标识。链式栈新结点的插入和栈顶结点的删除都是在链表的表头，即栈顶进行。
3.2.3 链式栈实现
#include <iostream>
#include<assert.h>
using namespace std;
// 使用带表头的单链表实现
struct LinkNode {
int data;
LinkNode* link;
LinkNode(LinkNode* ptr = NULL) { link = ptr; } // 仅初始化指针成员的函数
LinkNode(const int& item, LinkNode* ptr = NULL) { data = item; link = ptr; } // 初始化数据与指针成员函数
};
class LinkedStack {
private:
LinkNode* top;
public:
LinkedStack() : top(NULL) {} // 构造函数置空栈
~LinkedStack() { makeEmpty(); }; // 析构函数
void makeEmpty(); // 清空内存
void Push(const int& x); // 入栈
bool Pop(int& x); // 出栈
bool getTop(int& x)const; // 获得栈顶元素
bool IsEmpty()const { return (top == NULL) ? true : false; }
int getSize()const; // 求栈的元素个数
};
void LinkedStack::makeEmpty() {
LinkNode* p;
while (top != NULL) {
p = top;
top = top->link;
delete p;
}
};
void LinkedStack::Push(const int& x) {
top = new LinkNode(x, top); // 栈顶变为新结点
assert(top != NULL);
};
bool LinkedStack::Pop(int& x) {
if (IsEmpty() == true) return false;
LinkNode* p = top; // 暂存栈顶结点
top = top->link; // 栈顶指针退到新的栈顶位置
x = p->data;
delete p; // 删除top
return true;
};
bool LinkedStack::getTop(int& x) const {
if (IsEmpty() == true) return false;
x = top->data; // 栈不空则返回栈顶元素的值
return true;
};
int LinkedStack::getSize()const {
LinkNode* p = top;
int k = 0;
while (p != NULL) {
p = p->link; // 遍历链表
k++;
}
return k;
};
int main()
{
}
4. 递归
4.1 递归的概念
递归简单来说就是函数自己调用自己。
有三种情况常常用到递归：
4.1.1 定义是递归的
比如计算阶乘、幂函数、斐波拉契数列时，定义和计算都是递归的
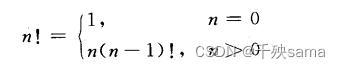
long Factorial(long n){
if(n == 0) return 1; // 终止条件
else return n*Factorial(n-1); // 递归
}
如计算 Factorial(5)时，首先进入函数判断5 != 0，计算5Factorial(4)，判断4 != 0，计算 4Factorial(3)，此时已经有54Factorial(3)，依次进行下去当Factorial(1)时，此时n==1,返回1，且不会进行递归调用函数，此时递归结束，Factorial(5)计算结果为54321。
4.1.2 数据结构是递归的
如单链表寻找最后一个结点时
LinkNode * FindRear(LinkNode *f){
if(f == NULL) return NULL;
else if(f->link ==NULL) return f;
else return FindRear(f->link);
}
又如返回给定值x的结点的地址
void search(LinkNode *f,int &x{
if(f == NULL) return NULL; // 搜索失败
else if(f->data == x) return f; // 符合条件
else Search(f->link,x); // 不符合条件，从下一个节点开始搜索
}
4.1.3 问题解法是递归的
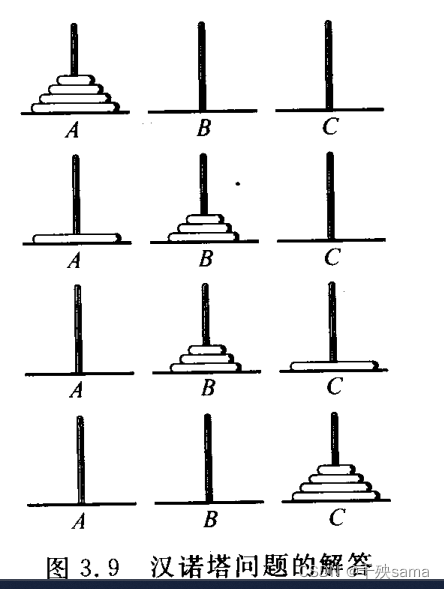
汉诺塔问题
n = 1时，将A直接移动到C。否则执行以下三步：
- 用C做过渡，将A上的（n - 1）个盘子移动到B上。
- 将A柱上的最后一个盘子放在C柱上。
- 用A柱作为过渡，将B柱上的（n - 1）个盘子移动到C柱上
代码实现
#include<string.h>
using namespace std;
void Hanoi(int n, string A, string B, string C) // A是起点，B是可以用的，C是终点
{
if (n == 1)
cout << " from " << A << " to " << C << endl; // 只有一个盘子，直接移动
else {
Hanoi(n - 1, A, C, B); // 将上面的n-1个盘子移动到B 此时A=1，C=0,B=N-1
cout << " from " << A << " to " << C << endl; // 最后一个盘子移动到C 此时A=0,C=1.B=N-1;
Hanoi(n - 1, B, A, C); // 将B柱n-1 个盘子移动到C柱 此时A=0,C=N,B=0
}
}
int main()
{
string A = "a";
string B = "b";
string C = "C";
int n = 3;
Hanoi(n, A, B, C);
return 0;
}
递归过程
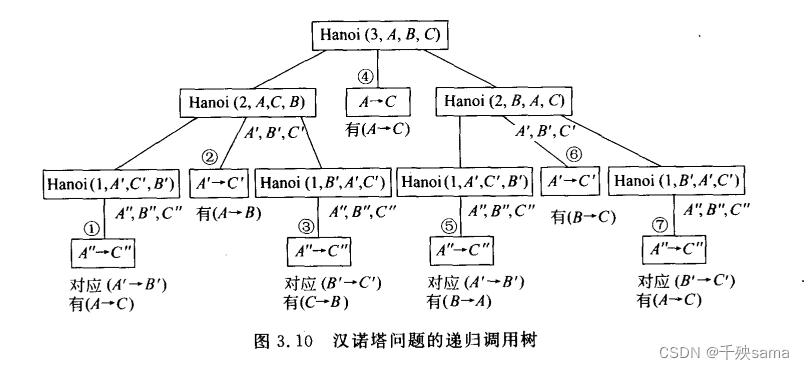
书上写得不是很好，推荐一篇博客
【看这一篇就够了】递归与汉诺塔问题(Hanoi)的超详细算法详解
5. 队列
5.1 队列的概念
只允许一端插入，在表的另一端删除。允许插入的一端叫队尾，允许删除的一端叫队头。如同售票排队一样，先进队列的先出队列。
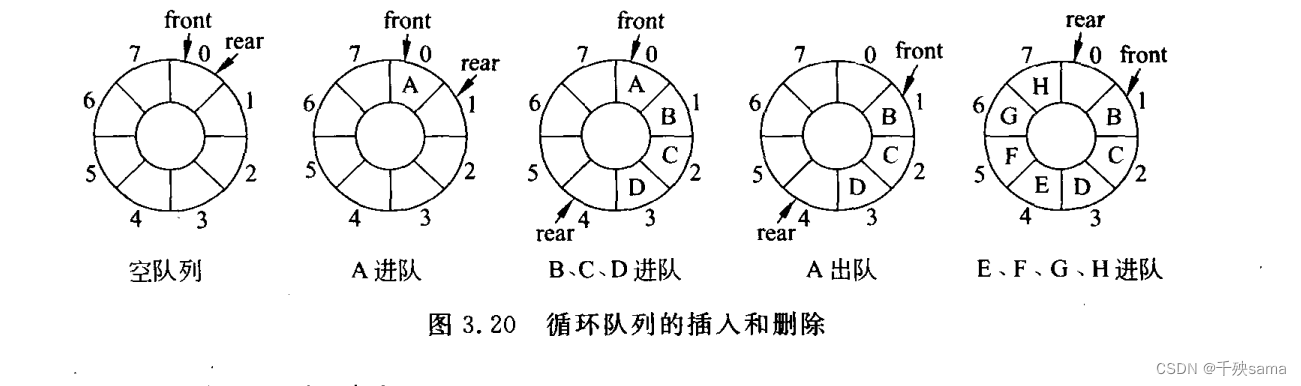
5.2 循环队列
5.2.1 循环队列的插入和删除
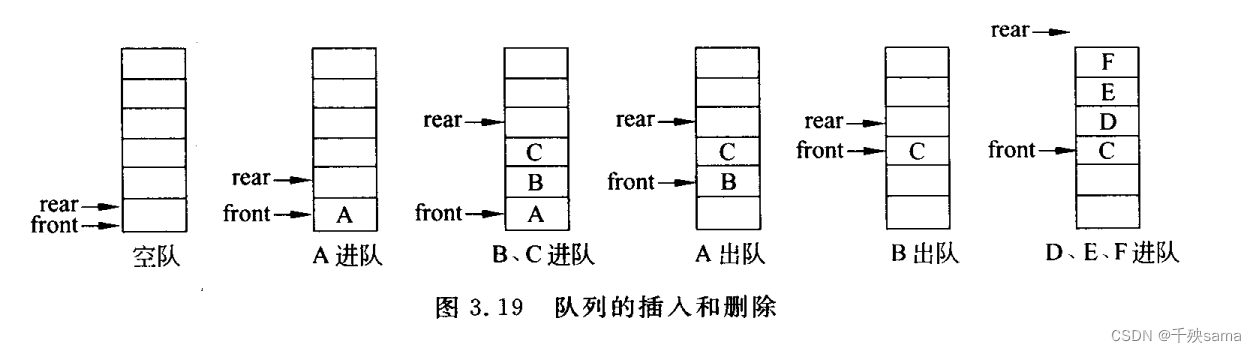
队列基于数组的存储表示称为顺序队列，利用一个一维数组进行存储，并使用rear 和 front两个指针，作为队尾和对头。初始化时front = rear = 0。加入新元素时，插入rear所指的位置，随后rear + 1，删除元素时，删除front所指的位置，随后front+1。这种队列会发生假溢出，所以使用循环队列充分利用内存空间。
队头指针进1 ：front = （front+1）% maxSize；
队尾指针进1： rear = （rear+1）% maxSize；
当 front == rear 时，队为空队列，当（rear+1）%maxSize == front 时，队满。
5.2.2 循环队列的实现
#include <iostream>
#include <assert.h>
using namespace std;
class SeqQueue {
private:
int rear; // 队尾
int front; // 队头
int* elements; // 存放数据
int maxSize; // 队列最大可容纳元素个数
public:
SeqQueue(int sz = 10); // 构造函数
~SeqQueue() { delete[] elements; } // 析构函数
bool EnQueue(const int& x); // 进队
bool DeQueue(int& x); // 出队
bool getFront(int& x); // 获得表头
void makeEmpty() { front = rear = 0; } // 清空
bool IsEmpty()const { return(front == rear) ? true : false;} //判断栈为空
bool IsFull()const { return((rear + 1) % maxSize == front) ? true : false; } // 判断栈满
int getSize()const { return (rear - front + maxSize) % maxSize; } // 获得队列元素
};
SeqQueue::SeqQueue(int sz):front(0),rear(0),maxSize(sz) {
// 建立一个最大具有maxSize个元素的空队列
elements = new int[maxSize];
assert(elements != NULL);
};
bool SeqQueue::EnQueue(const int& x) { // 进队
if (IsFull() == true) return false; // 若队列满则插入失败，返回
elements[rear] = x; // 插入队尾
rear = (rear + 1) % maxSize; // 队尾指针+1
return true;
}
bool SeqQueue::DeQueue(int& x) {
if (IsEmpty() == true) return false;
x = elements[front]; // 获得队头元素
front = (front + 1) % maxSize; // 队头+1
return true;
};
bool SeqQueue::getFront(int& x) {
if (IsFull() == true) return false;
x = elements[front]; // 返回队头元素
return true;
}
int main()
{
}
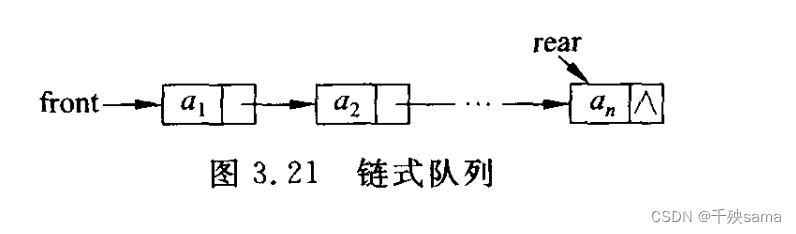
5.3 链式队列
基于单链表存储的队列。队列的队头指针指向第一个结点，队尾指针指向单链表的最后一个节点。
#include <iostream>
using namespace std;
// 使用带表头的单链表实现
struct LinkNode {
int data;
LinkNode* link;
LinkNode(LinkNode* ptr = NULL) { link = ptr; } // 仅初始化指针成员的函数
LinkNode(const int& item, LinkNode* ptr = NULL) { data = item; link = ptr; } // 初始化数据与指针成员函数
};
class LinkedQueue {
public:
LinkedQueue():rear(NULL),front(NULL){}
~LinkedQueue() { makeEmpty(); }
void makeEmpty();
bool EnQueue(const int& x); // 进栈
bool DeQueue(int& x); // 出栈
bool getFront(int x)const; // 查看队头
bool IsEmpty()const { return (front == NULL) ? true : false; } // 判断队列是否为空
int getSize()const; // 获得队列元素个数
private:
LinkNode* front, * rear; // 队头队尾指针
};
void LinkedQueue::makeEmpty()
{
LinkNode* p;
while (front != NULL) {
p = front;
front = front->link;
delete p;
}
};
bool LinkedQueue::EnQueue(const int& x)
{
if (front == NULL) { // 当front队头为空时
front = rear = new LinkNode(x);
if (front == NULL) {
cout << "error when enQueue!" << endl;
return false;
}
}
else {
rear->link = new LinkNode(x);
if (rear->link == NULL) return false;
rear = rear->link;
}
return true;
}
bool LinkedQueue::DeQueue(int& x)
{
if (IsEmpty() == true) return false;
LinkNode* p = front;
x = front->data;
front = front->link;
delete p;
return true;
}
bool LinkedQueue::getFront(int x) const
{
if (IsEmpty() == true) return false;
x = front->data;
return true;
}
int LinkedQueue::getSize() const
{
LinkNode* p = front;
int k = 0;
while (p != NULL) { p = p->link; k++; }
return k;
}
int main()
{
}
5.4 打印二项展开式
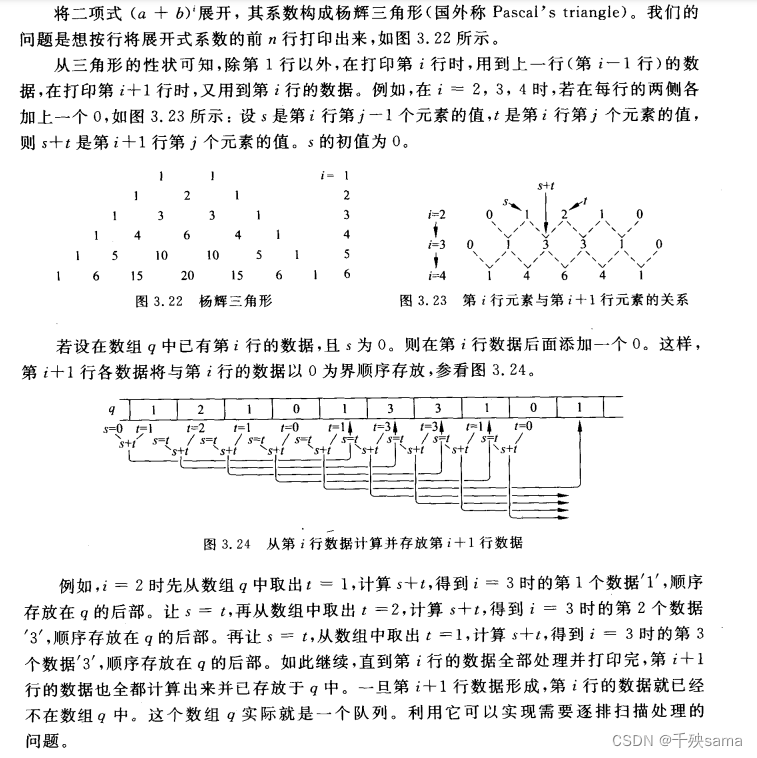
void YangVI(int n) {
Queue q(n + 1); // 建立队列对象并初始化
int s = 0; // 存放 S （s+t）^n 的s
int k = 0; // 作为每行队尾插入的0的工具人
int t; // 存放T S （s+t）^n 的t
int u; // 暂时存放下一行的根据(s+t)算出的数据
q.Enqueue(1); q.Enqueue(1); // 先把第一行插入
for (int i = 1; i <= n; i++) {
cout << endl;
q.EnQueue(k); // 在这一行的队尾插入一个0
for (int j = 1; j <= i + 2; j++) {
q.DeQueue(t); // 读取T的数据
u = s + t; // 计算下一行的数据
q.EnQueue(u); // 将算出的数据入队
s = t; // s变成他下一位数据
if (j != i + 2)cout << s << " "; // 打印除了0 的数据
}
}
}
扫一扫
505
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
