数据结构学习笔记（二）线性表

最新推荐文章于 2025-12-18 13:12:06 发布
原创 最新推荐文章于 2025-12-18 13:12:06 发布 · 483 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#数据结构 #学习 #笔记

文章目录

1. 前言

本系列笔记基于 清华大学出版社的《数据结构：用面向对象方法与C++语言描述》第二版进行学习。

2. 概念

线性表是一个有序序列，意味着每个表项是相继排列的，且每两个相邻表项之间都有直接前驱和直接后继的关系。线性表的第一个表项成为表头，第二个表项成为表尾。

3. 分类及父类实现

线性表的存储表示：顺序存储和链表存储方式。

线性表的类定义

template<class T>  // 模板类
class LinearList {

public:
	LinearList();
	~LinearList();
	virtual int Size() const = 0;					// 获取表能存储的最大长度
	virtual int Length() const = 0;					// 获取表当前长度
	virtual int Search(T& x)const = 0;			    // 搜索给定值X，返回表项
	virtual int Locate(int i)const = 0;			    // 搜索第i个元素的位置,返回表项序号
	virtual bool getData(int x, T& x)const = 0;		// 获取第i的表项的值，存储在数据x中
	virtual void setData(int i, T& x) = 0;			// 设置第i个表项的值x
	virtual bool Insert(int i, T& x) = 0;			// 在第i个表项后插入x
	virtual bool Remove(int i, T& x) = 0;           // 删除第i个表项
	virtual bool IsEmpty() const = 0;				// 判断表为空
	virtual bool IsFull() const = 0;				// 判断表是否已满
	virtual void Sort() = 0;						// 排序
	virtual void input() = 0;						// 输入
	virtual void output() = 0;						// 输出
	virtual LinearList<T> operator=(LinearList<T>& linearList) = 0;  // 复制
};

template 是模板类，一但声明了模板（template < typename T> ），就可以将类型参数用于类的成员函数和成员变量了。换句话说，原来使用 int、float、char 等内置类型的地方，都可以用类型参数来代替。

简述类模板函数模板template （typename T）

virtual int Locate(int i)const = 0;

virtual 是虚构函数，是面向对象属性的多态之一，简单来说就是在父类中声明该函数，在子类中进行实现。

C++ Virtual详解

const 和 = 0，参考

virtual IsEmpty() const=0中的const有什么用？

3.1 顺序表及其实现

顺序表是线性表基于数组的存储表示。

3.1.1 定义和特点

定义：把线性表中所有的表项按照其逻辑顺序依次存储到从计算机存储中指定存储位置开始的一块连续存储空间中。

特点：①表项的逻辑顺序和物理顺序一致，即第i个表项存储在第i个物理位置。②可以进行顺序访问，也可进行随机访问（即可以从第一个表项开始逐个访问，也可以按照表项的序号直接访问）。

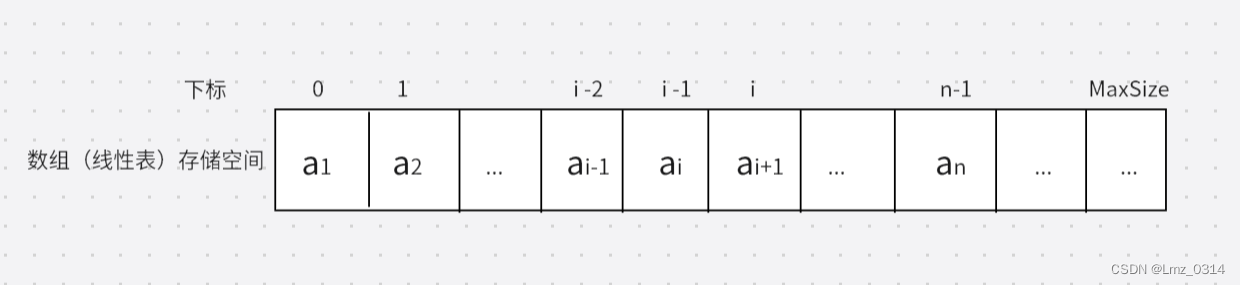
在这里插入图片描述
顺序表的静态存储

#define maxSize 100
typedef int T;
typedef struct {
	T data[maxSize];
	int n;
}SeqList;

顺序表的动态存储

typedef int T;
typedef struct {
	T* data;
	int maxSize, n;
}SeqList;

3.1.2 顺序表实现

#include <iostream>


using namespace std;
/*
template<class T>  // 模板类
class LinearList {

public:
	LinearList();
	~LinearList();
	virtual int Size() const = 0;					// 获取表能存储的最大长度
	virtual int Length() const = 0;					// 获取表当前长度
	virtual int Search(T& x)const = 0;			    // 搜索给定值X，返回表项
	virtual int Locate(int i)const = 0;			    // 搜索第i个元素的位置,返回表项序号
	virtual bool getData(int i, T& x)const = 0;		// 获取第i的表项的值，存储在数据x中
	virtual void setData(int i, T& x) = 0;			// 设置第i个表项的值x
	virtual bool Insert(int i, T& x) = 0;			// 在第i个表项后插入x
	virtual bool Remove(int i, T& x) = 0;           // 删除第i个表项
	virtual bool IsEmpty() const = 0;				// 判断表为空
	virtual bool IsFull() const = 0;				// 判断表是否已满
	virtual void Sort() = 0;						// 排序
	virtual void input() = 0;						// 输入
	virtual void output() = 0;						// 输出
	virtual LinearList<T> operator=(LinearList<T>& linearList) = 0;  // 复制
};
*/

const int defaultSize = 100;
template<class T>
class SeqList {
protected:
	T* data;										// 存放数组
	int maxSize;									// 最大可容纳表的项数
	int last;										// 当前已存表项的最后位置
public:
	SeqList(int sz = defaultSize);					// 构造函数
	SeqList(SeqList<T>& L);							// 复制构造函数
	~SeqList() { delete[] data; }					// 析构函数
	int Size()const { return maxSize; }				// 表最大可容纳表项个数
	void reSize(int newSize);						// 改变data数组空间大小
	int Length()const { return last + 1; }			// 表长度
	int Search(T& x)const;							// 搜索x的位置，并返回表项
	int Locate(int i)const;							// 定位第i个表项，返回表项序号
	bool getData(int i,T& x)const 
	{ if (i > 0 && i <= last + 1) { x = data[i - 1]; return true; } else return false; }	// 取第i个表项的值
	void setData(int i, T& x) 
	{ if (i > 0 && i < last + 1) x = data[i - 1]; }	// 设置第i个表项的值
	bool Insert(int i, T& x);						// 在第i个表项后插入x
	bool Remove(int i, T& x);						// 删除第i个表项，并把删除的值存储到x中
	bool IsEmpty() 
	{ return (last == -1) ? true : false; }			// 判断表是否为空
	bool IsFull()
	{ return (last == maxSize - 1) ? true : false; } //判断表是否已满
	void input();
	void output();
	SeqList<T> operator = (SeqList<T> &L);         // 重载=
};


template<class T>
SeqList<T>::SeqList(int sz) {
	if (sz > 0) {
		maxSize = sz;
		last = -1;
		data = new T[maxSize];
		if (data == NULL) 
		{
			cout << "内存分配错误!" << endl;
			exit(1);
		}
	}
}

template<class T>
SeqList<T>::SeqList(SeqList<T> &L) {
	maxSize = L.Size;
	last = L.Length - 1;
	T value;
	data = new T[maxSize];
	if (data == NULL)
	{
		cout << "内存分配错误!" << endl;
	}
	for (int i = 1; i <= last + 1; i++)
	{
		L.getData(i, value);		// 获取第i个数据的值，
		data[i - 1] = value;			// 存放在物理位置
	}
}

template<class T>
void SeqList<T>::reSize(int newSize) {
	if (newSize < 0) {
		cout << "无效的数组长度" << endl;
		return;
	}
	if (newSize != maxSize) {
		T* newArray = new T[newSize];
		if (newArray == NULL) {
			cout << "内存分配错误!" << endl; exit(1);
		}
		int n = last + 1;
		T* scrPtr = data;				// 指向原有数据
		T* destPrt = newArray;			// 指向新内存空间
		while (n--) *destPrt++ = *scrPtr++;  // 赋值，将新指针指向原有指针的内存空间
		delete []data;					// 删除老指针
		data = newArray;
		maxSize = newSize;
	}
}

template<class T>
int SeqList<T>::Search(T& x)const {
	for (int i = 0; i <= last; i++) {
		if (data[i] == x)return i + 1;	// 顺序搜索
	}
	return 0;							// 搜索失败
}

template<class T>
int SeqList<T>::Locate(int i)const {
	if (i > 0 && i <= last + 1) return i;  // 定位第i个表项的位置，这里的位置指物理位置
	else return 0;				
}

template<class T>
bool SeqList<T>::Insert(int i, T& x) {  // 插入第i个表项后
	if (last == maxSize - 1) {
		cout << "表满，不能插入" << endl;
		return false;
	}

	if (i < 0 || i > last + 1) {
		cout << "插入位置不合理，不能插入" << endl;
		return false;
	}

	for (int j = last; j >= i; j--) {
		data[j + 1] = data[j];		// 将数据依次后移一位
	}

	data[i] = x;
	last++;
	return true;
}


template<class T>
bool SeqList<T>::Remove(int i, T& x) {
	if (last == -1) return false;   // 表空，不能删除
	if (i < 1 || i > last + 1) return false;	// 参数i不合理
	x = data[i - 1];
	for (int j = i; j <= last; j++) {
		data[j - 1] == data[j];		// 将数据依次前移一位
	}
	last--;
	return true;
}

template<class T>
void SeqList<T>::input() {
	cout << "input data number:";
	while (1) {
		cin >> last;
		if (last <= maxSize - 1) break;
		cout << "input error, please input equal or less than" << maxSize - 1 << ":";
	}

	for (int i = 0; i <= last; i++) {
		cin >> data[i]; cout << "input the "<<i + 1<<" data" << endl;
	}

}

template<class T>
void SeqList<T>::output() {
	cout << "the last index：" << last << endl;
	for (int i = 0; i <= last; i++) {
		cout << "#" << i + 1 << ":" << data[i] << endl;
	}
}

template<class T>
SeqList<T> SeqList<T>::operator =(SeqList<T>& L) {
	maxSize = L.Size;
	last = L.Length - 1;
	T value;
	data = new T[maxSize];
	if (data == NULL)
	{
		cout << "内存分配错误!" << endl;
	}
	for (int i = 1; i <= last + 1; i++)
	{
		L.getData(i, value);		// 获取第i个数据的值，
		data[i - 1] = value;			// 存放在物理位置
	}
}


int main()
{
	SeqList<int> seq(5);
	seq.input();
	seq.output();

	seq.reSize(6);

	int testInsertA = 50;
	seq.Insert(1, testInsertA);
	seq.output();

	int testRemoveA;
	seq.Remove(2, testRemoveA);
	cout << testRemoveA << endl;
	seq.output();

	cout << seq.Search(testInsertA) << endl;

	return 0;
}

测试用的数据输入 是
4
10 20 30 40 50

输出结果
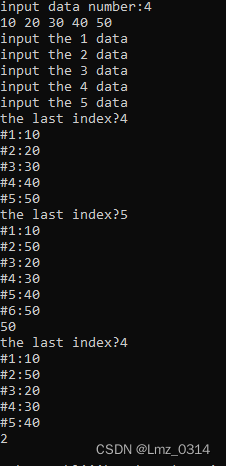
在这里插入图片描述

3.1.3 顺序表的性能分析

顺序表操作实现中，最复杂、最耗时的就是搜索、插入和删除运算。

ACN(average comparing number) 平均比较次数
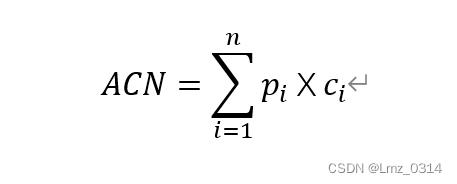
在这里插入图片描述
Pi指各个表项的搜索概率
Ci指找到该表项的比较次数

对于顺序表，搜索每个项的可能性都相同，即
P1=P2=…=PN= 1/N
搜索第1个表项的次数为1，第2个表项的次数是2，第n个表项的次数是n

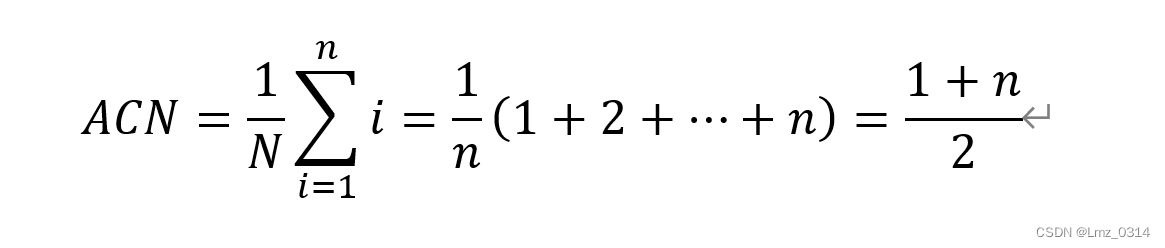
在这里插入图片描述

AMN(average moving number)平均移动次数
将新表项插入第i个表项，必须从后向前循环，并逐个相后移动n-i个表项。最好的情况是在第n个表项后追加新表项，移动表项个数为0，最坏的情况是在第1个表项后追加新表项，移动项数为n个。
插入概率相等的情况下，

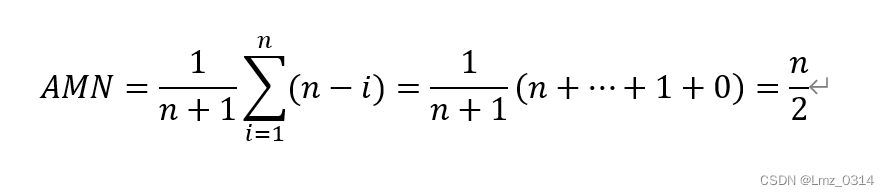
在这里插入图片描述
删除第i个表项时，必须从前往后循环，逐个移动n-i个项。最好的情形时删除最后的第n个表项，最差的情况时删除第1个表项，移动表项个数为n-1。删除概率相等时
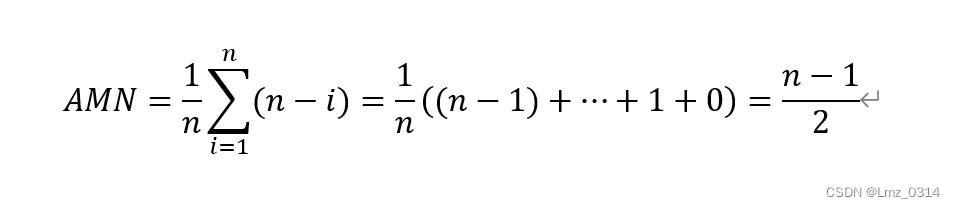
在这里插入图片描述

3.2 单链表及其实现

3.2.1 定义和特点

定义：单链表用来表示线性表时，用指针表示节点间的逻辑关系。因此一个存储节点包含两部分，数据域和指针域。
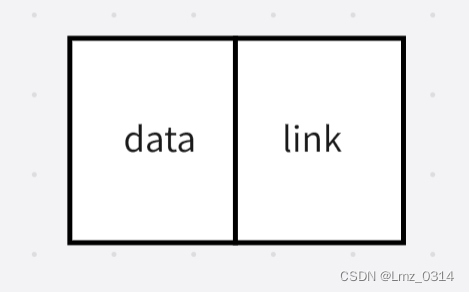
在这里插入图片描述
data部分称为数据域，用于存储线性表的一个数据元素，link部分称为指针域或链域，用于存放指针，该指针指向链表中下一个节点的开始存储地址。
在这里插入图片描述
特点：长度可以方便的进行扩充。链表中数据元素的顺序与链表表示中节点的物理顺序可能不一致，一般通过单链表的指针将各个元素按照逻辑顺序连接起来。

在这里插入图片描述

（1）复合类

class List;

class LinkNode {
    friend class List;
private:
    int data;
    LinkNode* link;
};

class List {
public:
    //... 链表操作
private:
    LinkNode* first;
};

（2） 嵌套类

class List {
public:
    // 链表操作

private:
class LinkNode {
public:
    int data;               // 数据域
    LinkNode *link;         // 指针域
};
LinkNode* first;            // 指针头
};

（3）基类和派生类


class LinkNode {
protected:
    int data;
    LinkNode* link;
};

class List :public LinkNode {
private:
    LinkNode* first;
public:
    // 链表操作
};

（4）用结构体struct定义LinkNode类

struct LinkNode {
    int data;
    LinkNode* link;
};

class List {
private:
    LinkNode* first;
public:
    // 链表操作
};

3.2.2 单链表的插入

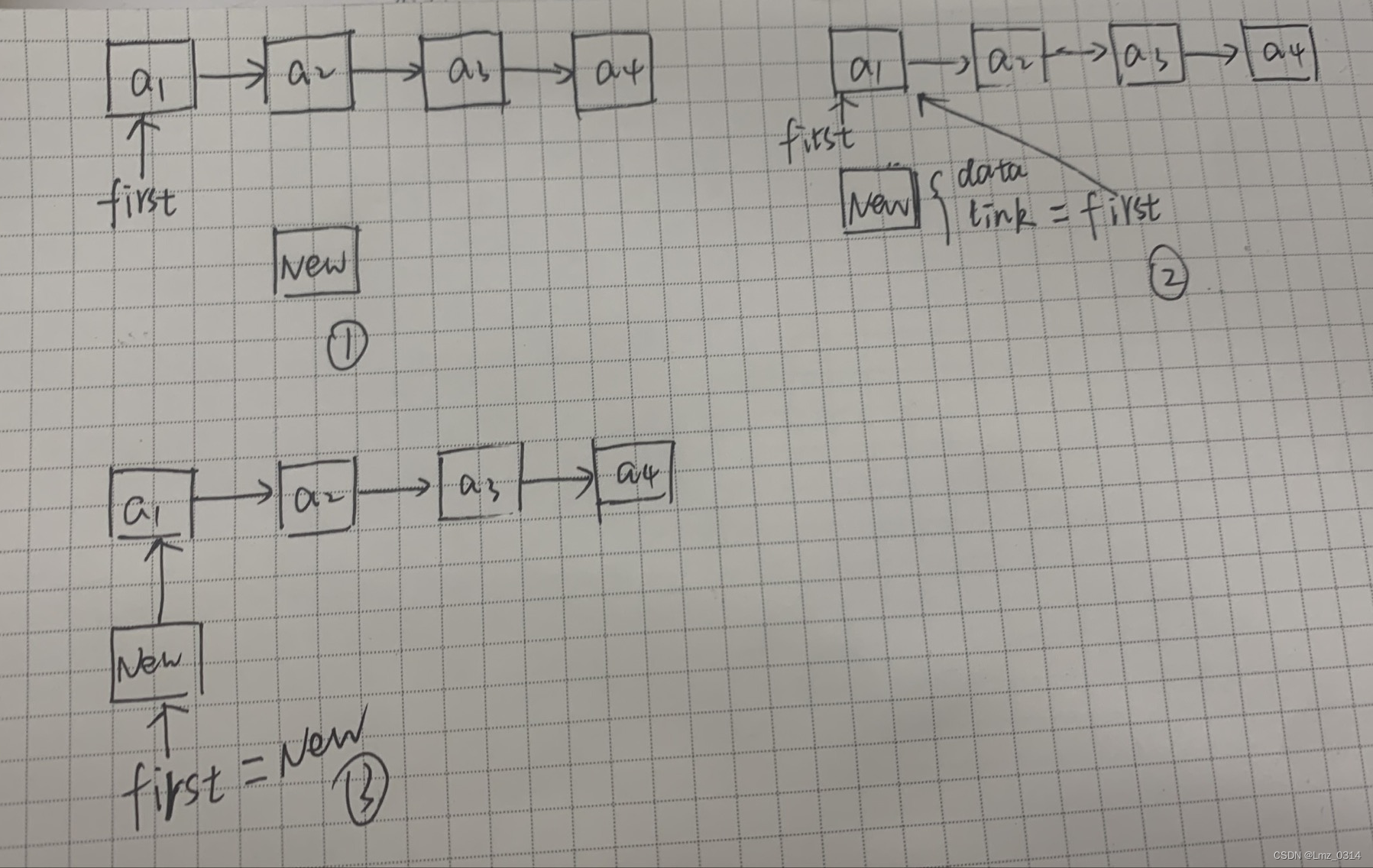
（1）插入第一个节点前，则需要修改first指针。
newNode->link = first;
first = newNode;

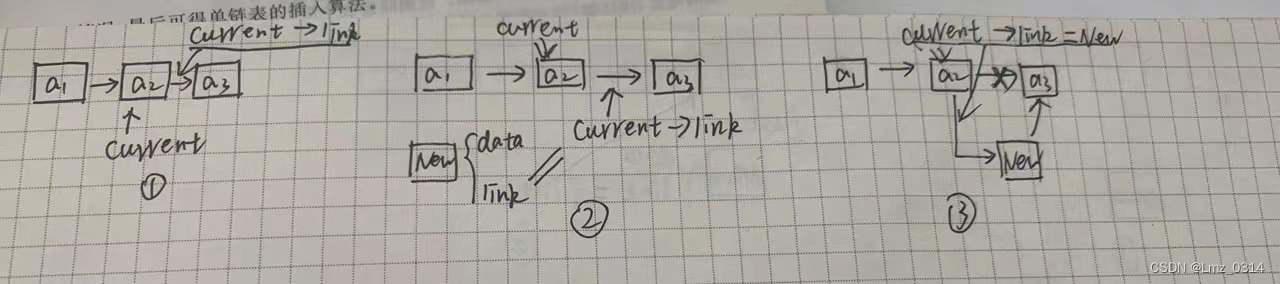
在这里插入图片描述
(2)插入中间节点ai之后，首先让一个检测指针指向ai，再将新节点插入ai节点之后
newNode->link = current->link;
current->link= newNode;
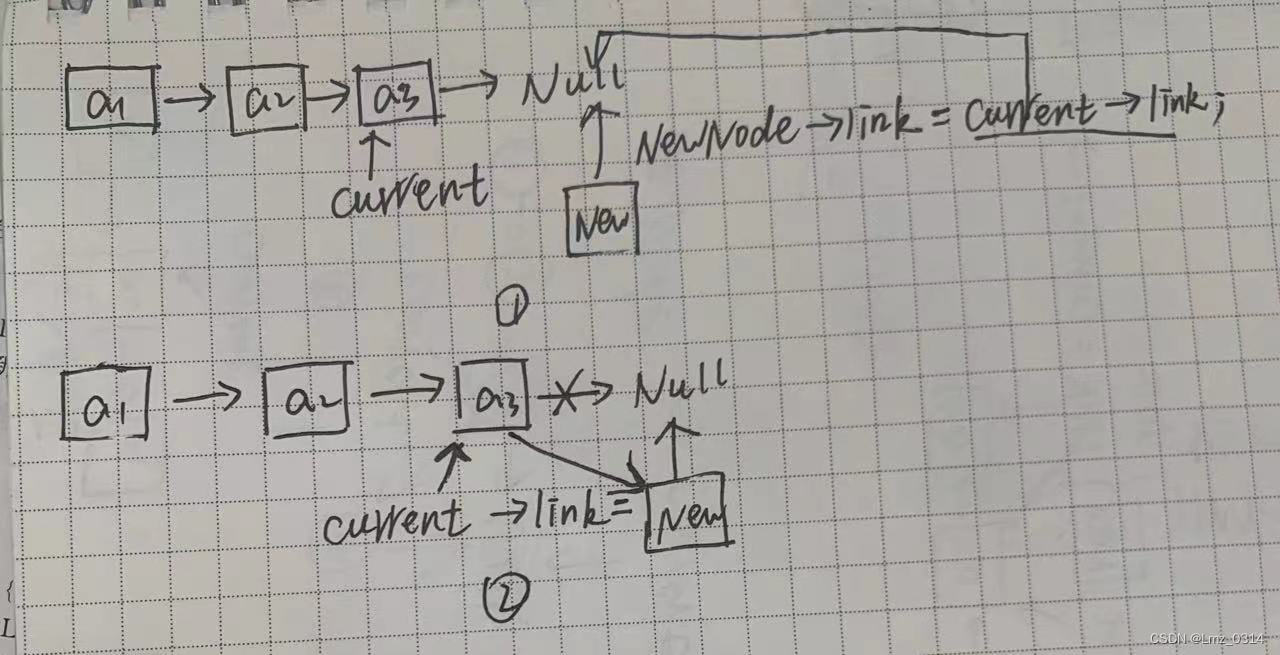
在这里插入图片描述
(3)插入最后一个结点时，新节点追加到表尾。
newNode ->link = current->link;
current->link = newNode;
在这里插入图片描述
单链表的插入算法

bool List::Insert(int i, int& x) {
    if (first == NULL || i == 0) 
    {
        // insert to first node
        LinkNode* newNode = new LinkNode(x);

        if (newNode == NULL) 
        {
            cout << "error when allocate memory" << endl;
            exit(1);
        }

        newNode->link = first;
        first = newNode;
    }
    else
    {
        LinkNode* current = first;      // search for node
        for (int k = 1; k < i; k++)
        {
            if (current == NULL)
            {
                cout << "error insert index" << endl;
                break;
            }
            else current = current->link;  // link to next node
        }

        if (current == NULL)
        {
            cout << "error insert index" << endl;
            return false;
        }
        else
        {
            LinkNode* newNode = new LinkNode(x);
            if (newNode == NULL)
            {
                cout << "error when allocate memory" << endl;
                exit(1);
            }
            newNode->link = current->link;
            current->link = newNode;

        }

    }

    return true;
}

3.2.3 单链表的删除

（1）在首结点处删除，使用指针del保存首结点，再将first指向下一个结点，最后删除原来的首结点。
del = first;
first = first ->link;
delete del;
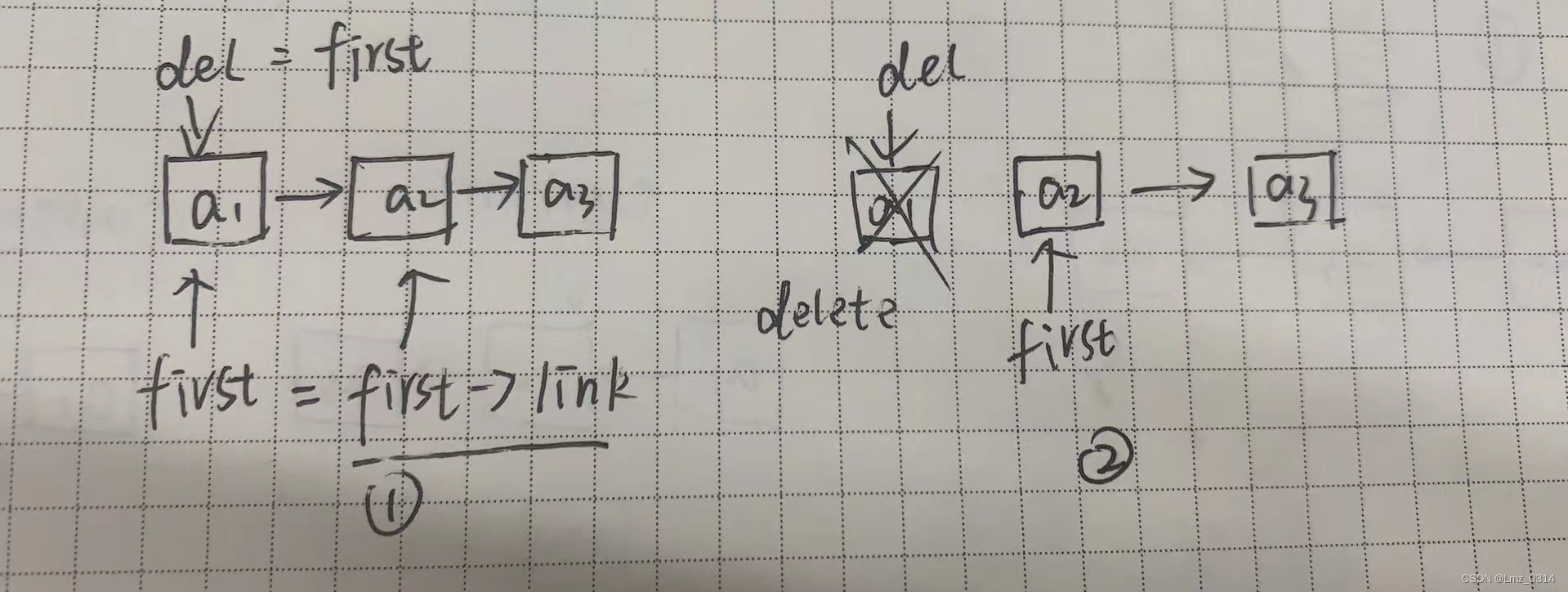
在这里插入图片描述
(2）在链表中间或尾部删除，用del存储第i个节点的地址，将i-1的结点指向i+1的结点的地址。再删去del。
del = current -> link;
current -> link = del -> link;
delete del;
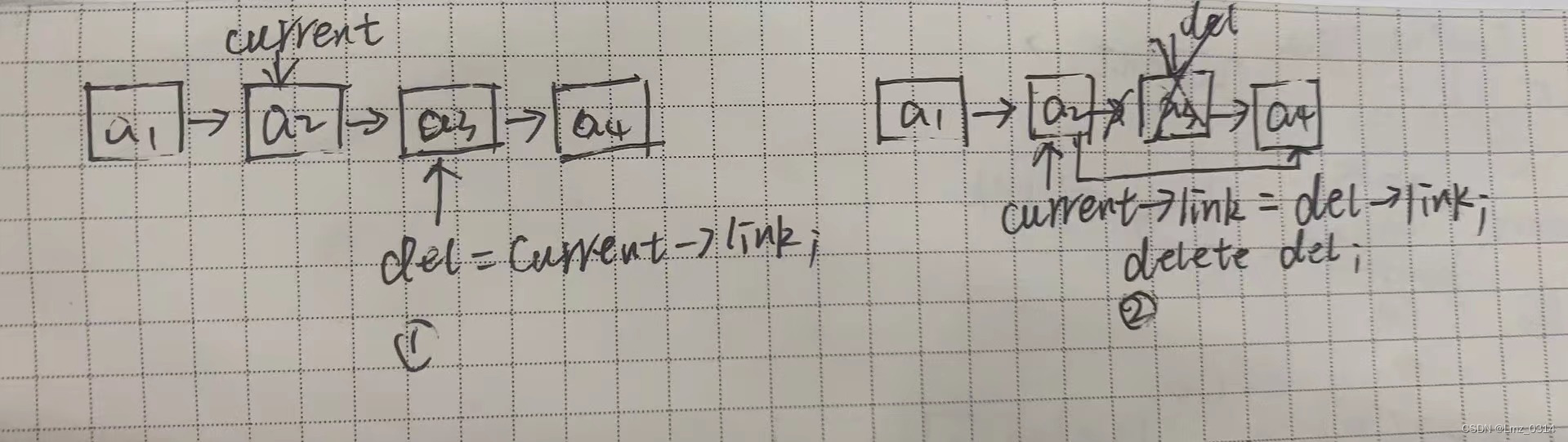
在这里插入图片描述
单链表的删除算法

bool List::Remove(int i, int& x) 
{
    LinkNode* del;
    LinkNode* current;
    if (i <= 1) 
    {
        del = first;
        first = first->link;
    }
    else 
    {
        current = first;
        for (int k = 1; k < i - 1; k++) 
        {  
            // loop for looking for Node which index is (i-1)
            if (current->link == NULL) break;
            else current = current->link;
        }
        if (current == NULL || current->link == NULL) {
            cout << "error delete index!" << endl;
            return false;
        }
        del = current->link;
        current->link = del->link;
    }

    x = del->data;
    delete del;
    return true;
}

可以使用带表头的单链表，则单链表的插入和删除在多种情况上操作都相同。
即插入：

newNode -> link = current -> link;
current -> link = newNode;

删除：
del = current->link;
current->link = del->link;
delete del;

3.2.4 单链表的实现

前插法是指每次输入新节点总是在表的前端进行，这样插入的逻辑顺序与输入数据的顺序正好相反。
后插法是指每次输入新节点总是插入到链表的尾端，数据中的逻辑顺序和输入顺序完全一致。

复制构造函数的思路（一次循环为例）
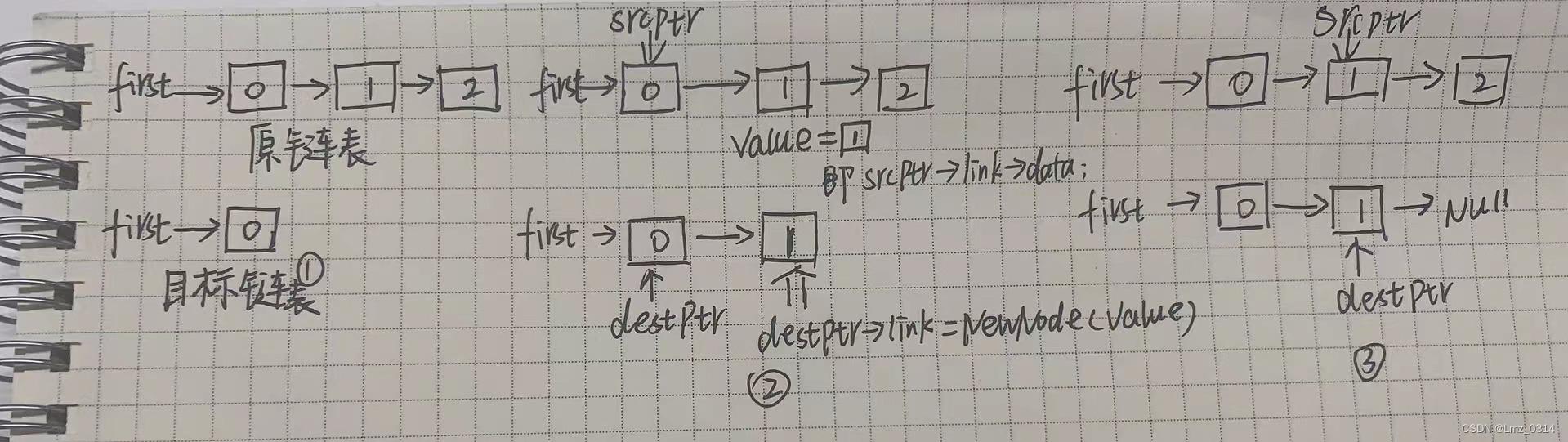
在这里插入图片描述
代码实现

#include <iostream>

using namespace std;

// 使用带表头的单链表实现
template<class T>
struct LinkNode {
    T data;
    LinkNode* link;
    LinkNode(LinkNode<T>* ptr = NULL) { link = ptr; }  // 仅初始化指针成员的函数
    LinkNode(const T& item, LinkNode<T>* ptr = NULL) { data = item; link = ptr; }   // 初始化数据与指针成员函数
};

template<class T>
class List {                                      // 实现单链表
public:
    List() { first = new LinkNode<T>; }           // 构造函数，使初始指针指向表头结点
    List(const T& x) { first = new LinkNode<T>(x); } // 构造函数，使初始数据为x
    List(List<T>& L);                             // 复制构造函数
    ~List() { makeEmpty(); }                      // 析构函数，释放所有内存
    void makeEmpty();                             // 释放内存
    int Length()const;                            // 计算链表长度
    LinkNode<T>* getHead()const { return first; } // 获得附加头结点的地址
    LinkNode<T>* Search(T x);                     // 搜索含数据x的元素
    LinkNode<T>* Locate(int i);                   // 搜索第i个元素的地址
    bool getData(int i, T& x)const;               // 获得第i个元素的指，存储到x中
    void setData(int i, T& x);                    // 设置第i个元素的指
    bool Insert(int i, T& x);                     // 在第i个元素后面插入x
    bool Remove(int i, T& x);                     // 删除第i个元素后的值，并将值返回到x
    bool IsEmpty()const { return first->link = NULL ? true : false; } // 判断表是否为空
    bool IsFull()const { return false; }          // 因为插入是申请新内存空间，所以表不会满（内存超了除外）
    void Sort();                                  // 排序
    void inputFront(T endTag);                            // 前插输入
    void inputRear(T endTag);                             // 后插输入
    void output();                                // 输出
    List<T>& operator=(List<T>& L);               // 重载函数
protected:
    LinkNode<T>* first;                           // 表的头指针
};

template<class T>
List<T>::List(List<T>& L) {
    T value;
    LinkNode<T>* srcptr = L.getHead();            // 获得头指针
    first = new LinkNode<T>;
    LinkNode<T>* destptr = first;
    while (srcptr->link != NULL) {
        value = srcptr->data;
        destptr->link = new LinkNode<T>(value);
        destptr = destptr->link;
        srcptr = srcptr->link;
    }
    destptr->link = NULL;
};



template<class T>
void List<T>::makeEmpty() {
    // 将列表置位空
    LinkNode<T>* q;
    while (first->link != NULL) {
        q = first->link;
        first->link = q->link;
        delete q;
    }
};

template<class T>
int List<T>::Length()const {  // 返回链表长度
    LinkNode<T>* p = first->link;
    int count = 0;
    while (p!= NULL) {
        p = p->link;
        count++;
    }
    return count;
};

template<class T>
LinkNode<T>* List<T>::Search(T x) { // 返回匹配结点的地址，如果没有则返回null
    LinkNode<T>* current = first->link;
    while (current != NULL)
        if (current->data = x) break;
        else current = current->link;
    return current;
};

template<class T>
LinkNode<T>* List<T>::Locate(int i) {
    if (i < 0) return NULL;         // 返回第i个结点的地址，如果非法则返回null
    LinkNode<T>* current = first;
    int k = 0;
    while (current->link != NULL && k < i) {
        current = current->link;
        k++;
    }
    return current;
};

template<class T>
bool List<T>::getData(int i, T& x)const {
    if (i <= 0) return NULL;         // 取第i个结点的值
    LinkNode<T>* current = Locate(i);
    if (current == NULL) return false;
    else { x = current->data; return true; }
};


template<class T>
void List<T>::setData(int i, T& x) {
    if (i <= 0) return;
    LinkNode<T>* current = Locate(i);
    if (current == NULL) return;
    else current->data = x;
};

template<class T>
bool List<T>::Insert(int i, T& x) { // 将结点插入到第i个结点之后
    LinkNode<T>* current = Locate(i);
    if (current == NULL) return false;
    LinkNode<T>* newNode = new LinkNode<T>(x);
    if (newNode == NULL) { cout << "error when allocate memory"; exit(1); }
    newNode->link = current->link;
    current->link = newNode;
    return true;
};

template<class T>
bool List<T>::Remove(int i, T& x) { // 删除第i个结点
    LinkNode<T>* current = Locate(i - 1);  // 找到第i个结点的前一个
    if (current == NULL || current->link == NULL) return false;

    LinkNode<T>* del = current->link; // 找到要删除的结点
    x = del->data;
    current->link = del->link;
    delete del;
    return true;
};

template<class T>
void List<T>::output() {   // 输出链表
    LinkNode<T>* current = first->link;
    int count = 0;
    while (current != NULL) {
        cout << "[" << count+1 << "]: " << current->data << endl;
        current = current->link;
        count++;
    }
};

template<class T>
void List<T>::inputFront(T endTag) {
    // endTag 是输入结束的标识符，如果输入规定的endTag，则结束输入
    LinkNode<T>* newNode;
    T val;
    makeEmpty();
    while (val != endTag) {
        newNode = new LinkNode<T>(val);
        if (newNode == NULL) { cout << "error when allocate memory!" << endl; exit(1); }
        newNode->link = first->link;        // 插入队伍的最前端
        first->link = newNode;              // 首指针指向新节点
        cin >> val;
    }
};  

template<class T>
void List<T>::inputRear(T endTag) {
    LinkNode<T>* newNode; 
    LinkNode<T>* last;
    T val;
    makeEmpty();

    cin >> val;
    last = first;

    while (val != endTag) {
        newNode = new LinkNode<T>(val);
        if (newNode == NULL) { cout << "error when allocate memory!" << endl; exit(1); }
        last->link = newNode;         // 当前的表尾指向新节点
        last = newNode;               // 表尾变成新节点
        cin >> val;
    }
    last->link = NULL;
};

int main()
{
    List<int> *testListFront = new List<int>();
    testListFront->inputRear(0);
    testListFront->output();
    int x1 = 5;
    testListFront->Insert(4, x1);
    testListFront->output();
    int a1 = 0;
    testListFront->Remove(1, a1);
    testListFront->output();

    List<int> *testListRear = new List<int>();
    testListRear->inputRear(0);
    testListRear->output();
    int x2 = 5;
    testListRear->Insert(4, x2);
    testListRear->output();
    int a2= 0;
    testListRear->Remove(1, a2);
    testListRear->output();

}

3.3 循环链表定义和特点

循环链表与单链表的区别在链表中表尾结点的link域不是NULL，而是存放了指向开始的指针。这样只需要知道一个结点的位置，就能遍历表中其他任一结点。

在这里插入图片描述
循环链表与链表基本类似，主要在判断current是否到达链表的表尾时，不是判断current->link = NULL，而是判断current->link = first。

3.3.1 循环链表的类定义

struct CircLinkNode {
    int data;
    CircLinkNode* link;
    CircLinkNode(CircLinkNode* next = NULL) :link(next) {}
    CircLinkNode(int d, CircLinkNode* next = NULL) :data(d), link(next) {}
};


class CircList {
public:
    CircList() { first = new CircLinkNode; last = first; }
    CircList(const int& x) { first = new CircLinkNode(x); }                   // 构造函数
    CircList(CircList& L);               // 复制构造函数
    ~CircList();                            // 析构函数
    int Length()const;                      // 计算链表长度
    bool IsEmpty() { return first->link == first ? true : false; } // 判断表空
    CircLinkNode* getHead()const { return first; };
    void setHead(CircLinkNode* p);       // 设置表头地址
    CircLinkNode* Search(int* x);          // 搜索x在表中位置
    CircLinkNode* Locate(int i);         // 定位第i个元素的地址
    int* getData(int i);                      // 获得第i个元素的值
    void setData(int i);                    // 用x修改第i个元素的值
    bool Insert(int i, int& x);               // 在第i个元素后插入x
    bool Remove(int i, int& x);               // 删除第i个元素，存储该元素值到x
private:
    CircLinkNode* first;                 // 头指针
    CircLinkNode* last;                  // 尾指针
};

3.3.2 循环链表的实现

实现函数遵循：主要在判断current是否到达链表的表尾时，不是判断current->link = NULL，而是判断current->link = first，并且注意last指针要指向表头。其余操作与单链表基本无差异。

3.4 双向链表定义和特点

双向链表又称双链表。双向链表中每个结点都有两个链指针，一个指向直接前驱，一个指向直接后驱。

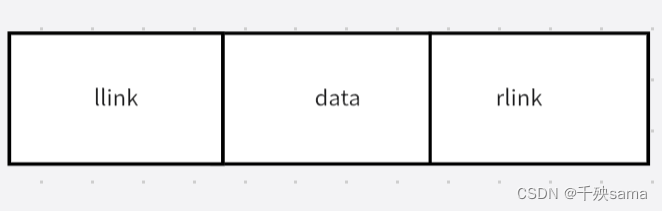
在这里插入图片描述

3.4.1 双向链表的类定义

struct DblNode {
    int data;
    DblNode* lLink;
    DblNode* rLink;
    DblNode(DblNode *left = NULL, DblNode* right = NULL):lLink(left),rLink(right){} // 构造函数
    DblNode(int value, DblNode* left = NULL, DblNode* right = NULL) :data(value), lLink(left), rLink(right) {}
};

class DblList {
public:
    DblList(int uniqueVal);             //构造函数：建立附加头结点
    ~DblList();                         //析构函数：释放所用内存
    int Length()const;                  // 返回链表长度
    bool IsEmpty() { return first->rLink == first; } // 判断表是否为空
    DblNode* getHead()const { return first; }        // 获得表头
    void setHead(DblNode* ptr) { first = ptr; }     // 设置表头地址
    DblNode* search(const int& x);                  // 搜索x的地址
    DblNode* Locate(int i, int d);                  // 搜索第i个结点地址的值，d=1则按前驱搜索，d!=1 按后驱搜索
    bool Insert(int i, const int& x, int d);        // 在第i个结点地址后面插入x，d=1则按前驱搜索，d!=1 按后驱搜索
    bool Remove(int i, int& x, int d);              // 删除第i个结点，d=1则按前驱搜索，d!=1 按后驱搜索
private:
    DblNode* first;
};

3.4.2 双向循环链表插入

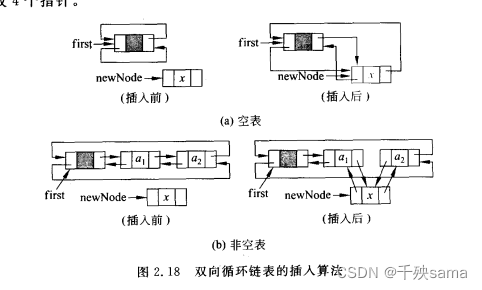
在这里插入图片描述

bool DblList::Insert(int i, const int& x, int d) {
    DblNode* current = Locate(i, d);  // 寻找到第i个结点
    if (current == NULL) return false;  // 插入结点不合理
    DblNode* newNode = new DblNode(x);
    if (newNode == NULL) { cout << "error when allocate memory"; exit(1); }

    if (d == 0)     // 前驱插入
    {
        newNode->lLink = current->lLink;
        current->lLink = newNode;
        newNode->lLink->rLink = newNode;
        newNode->rLink = current;
    }
    else
    {
        newNode->rLink = current->rLink;
        current->rLink = newNode;
        newNode->rLink->lLink = newNode;
        newNode->lLink = current;
    }
    return true;
};

3.4.2 双向循环链表删除

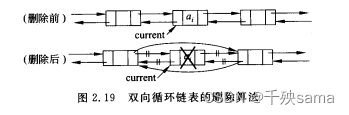
在这里插入图片描述

bool DblList::Remove(int i, int &x, int d) {
    DblNode* current = Locate(i, d);
    if (current == NULL) return false;
    current->rLink->lLink = current->lLink;
    current->lLink->rLink = current->rLink;
    x = current->data; 
    delete current;
    return true;
};

3.4.3 单链表的实现

#include <iostream>

using namespace std;

struct DblNode {
    int data;
    DblNode* lLink;
    DblNode* rLink;
    DblNode(DblNode *left = NULL, DblNode* right = NULL):lLink(left),rLink(right){} // 构造函数
    DblNode(int value, DblNode* left = NULL, DblNode* right = NULL) :data(value), lLink(left), rLink(right) {}
};

class DblList {
public:
    DblList(int uniqueVal);             //构造函数：建立附加头结点
    ~DblList();                         //析构函数：释放所用内存
    int Length()const;                  // 返回链表长度
    bool IsEmpty() { return first->rLink == first; } // 判断表是否为空
    DblNode* getHead()const { return first; }        // 获得表头
    void setHead(DblNode* ptr) { first = ptr; }     // 设置表头地址
    DblNode* Search(const int& x);                  // 搜索x的地址
    DblNode* Locate(int i, int d);                  // 搜索第i个结点地址的值，d=0则按前驱搜索，d=1 按后驱搜索
    bool Insert(int i, const int& x, int d);        // 在第i个结点地址后面插入x，d=0则按前驱搜索，d=1 按后驱搜索
    bool Remove(int i, int& x, int d);              // 删除第i个结点，d=0则按前驱搜索，d=1 按后驱搜索
private:
    DblNode* first;
};

DblList::~DblList() {



}

DblList::DblList(int uniqueVal) {
    // 构造函数：建立双向循环链表的附加头结点，包含一个特定情况的值
    first = new DblNode(uniqueVal);
    if (first == NULL) { cout << "error when allocate memory!"; }
    first->lLink = first->rLink = first;            // 初始化左右指针域地址
};

int DblList::Length()const {        // 返回链表长度
    DblNode* current = first->rLink;
    int count = 0;
    while (current != first) { current = current->rLink; count++; }
    return count;
};

DblNode* DblList::Search(const int& x) {
    DblNode* current = first->rLink;        // 获得首结点
    while (current != first && current->data != x) {
        current = current->rLink;
    }
    if (current != first) return current;
    else return NULL;           
};

DblNode* DblList::Locate(int i, int d) {
    //搜索第i个结点地址的值，d = 0则按前驱搜索，d = 1 按后驱搜索
    if (first->rLink == first || i == 0) return first;
    DblNode* current = NULL;
    if (d == 0) {
        current = first->lLink;
        for (int j = 1; j < i; j++) {
            if (current == first) break;
            current = current->lLink;
        }
    }
    if (d == 1) {
        current = first->rLink;
        for (int j = 1; j < i; j++) {
            if (current == first) break;
            current = current->rLink;
        }
    }
    
    if (current != first || current != NULL) return current;
    else return NULL;
};

bool DblList::Insert(int i, const int& x, int d) {
    DblNode* current = Locate(i, d);  // 寻找到第i个结点
    if (current == NULL) return false;  // 插入结点不合理
    DblNode* newNode = new DblNode(x);
    if (newNode == NULL) { cout << "error when allocate memory"; exit(1); }

    if (d == 0)     // 前驱插入
    {
        newNode->lLink = current->lLink;
        current->lLink = newNode;
        newNode->lLink->rLink = newNode;
        newNode->rLink = current;
    }
    else
    {
        newNode->rLink = current->rLink;
        current->rLink = newNode;
        newNode->rLink->lLink = newNode;
        newNode->lLink = current;
    }
    return true;
};


bool DblList::Remove(int i, int &x, int d) {
    DblNode* current = Locate(i, d);
    if (current == NULL) return false;
    current->rLink->lLink = current->lLink;
    current->lLink->rLink = current->rLink;
    x = current->data; 
    delete current;
    return true;
};



int main()
{
   

}

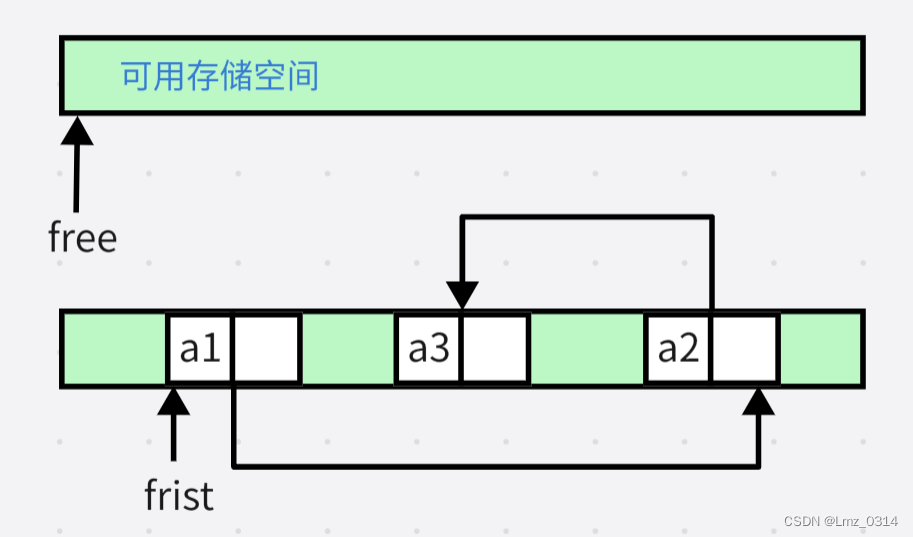
3.5 静态链表定义和特点

使用结点（数据和链表）数组存放数据，但存储位置是随机的。 数组中数据关系通过一个整型变量存储。

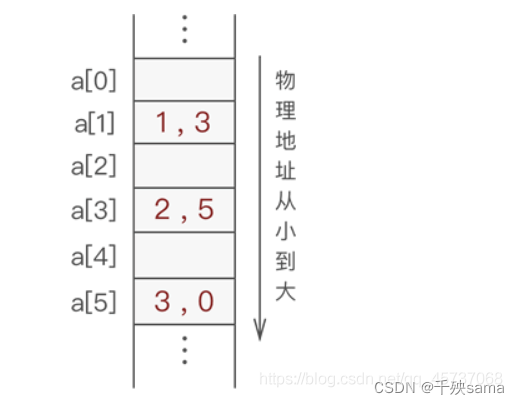
在这里插入图片描述
如 a[1]存储了数据1，指针存储了地址3，所以a[3]就是下一个存储的数据2，指针存储了地址5，所以a[5]就是下一个存储的数据3，存储了指针地址0，一般0不存储数据，所以链表结束。

此处使用地址-1作为链表结束的标识符。

3.5.1 静态链表的实现

#include <iostream>

struct SLinkNode {
    int data;       // 存储数据
    int link;       // 存储链接指针
};

const int maxSize = 10;

class StaticList {
    SLinkNode elem[10];     // 静态链表数组
    int avil;               // 当前分配空间的首地址
public:
    void InitList();        // 初始化函数
    int Length();           // 计算链表长度
    int Search(int x);      // 查找某个值
    int Locate(int i);      // 查找第i个结点
    bool Append(int x);     // 在表尾追加一个值
    bool Insert(int i, int x); // 在第i个结点后插入x
    bool Remove(int i);        // 释放第i个结点的
    bool IsEmpty();            // 判断链表是否为空
};


void StaticList::InitList() {
    elem->link = -1; 
    avil = 1;           // 当前可分配空间从1开始建立带表头结点的空链表
    for (int i = 1; i < maxSize - 1; i++)
    {
        elem[i].link = i + 1;       // 构建空闲链接表
    }
    elem[maxSize - 1].link = -1;    // 链表收尾
};

int StaticList::Length() {
    int p = elem[0].link;
    int i = 0;
    while (p != -1) {
        p = elem[p].link;
        i++;
    }
    return i;
};

bool StaticList::IsEmpty() {
    // 判断表是否为空
    if (elem[0].link == -1) return true; // 表头存储的下一个节点的下标是-1
    else return false;
};


int StaticList::Search(int x)
{
    int p = elem[0].link;
    while (p != -1) {
        if (elem[p].data == x) {
            break;
            return p;
        }
        else p = elem[p].link;
    }
    return 0;
};

int StaticList::Locate(int i) {
    if (i < 0) return -1;
    if (i == 0) return 0;
    int j = 1;
    int p = elem[0].link;
    while (p != -1 && j < i) {
        p = elem[p].link;
        j++;
    }
    return p;
};

bool StaticList::Append(int x) {
    if (avil == -1) return false;       // 无可使用的存储位置
    int q = avil;
    avil = elem[avil].link;
    elem[q].data = x;
    elem[q].link = -1;
    int p = 0;
    while (elem[p].link != -1)          // 寻找之前的表尾
        p = elem[p].link;
    elem[p].link = q;                   // 把新节点设成新表尾
    return true;
};


bool StaticList::Insert(int i, int x) {
    int p = Locate(i);
    if (p == -1) return false;
    int q = avil;
    avil = elem[avil].link;
    elem[q].data = x;
    elem[q].link = elem[p].link;  
    elem[p].link = q;
    return true;
};

bool StaticList::Remove(int i) {
    int p = Locate(i - 1);
    if (p == -1) return false;
    int q = elem[p].link;
    elem[p].link = elem[q].link;
    elem[q].link = avil;
    avil = q;
    return true;
};


int main()
{

}
千殃sama
关注
数据结构学习笔记之线性表（02）
✅ Java 开发工程师，从事 Web 应用程序的研发，擅长 Spring、SpringBoot 等技术。 ✅ 热爱编程，业余时间学习新知识，通过 优快云 记录学习心得和笔记内容。
01-12 697
第二章：数据结构之线性表 1.1、线性表相关概念 （1）线性表定义 线性表：线性表是由n个相同数据特点的元素组成的有限序列。 线性表中，元素的个数称为线性表的长度 表长等于0，则称为空表 线性表特点： 线性表中，数据元素都是具有相同性质的。 线性表存在唯一的头结点。 线性表存在唯一的尾节点。 线性表中，除了头尾两个节点外，其余节点都有且仅有一个前驱节点，一个后继节点。 1.2、线性表的顺序表示 （1）顺序表定义 线性表的顺序表示，
数据结构学习笔记-线性表
大白糖奶兔的Blog
07-23 817
线性表 Ptrl == Pointer 顺序存储结构定义 #define MaxSize 100 struct LNode { int data[MaxSize];//容量为100的顺序线性表 int Last;//最后一个元素的下标 }; typedef struct LNode* List;//结构体类型的指针，指向结构体 List PtrL;//线性表结构的指针 初始化 C List MakeEmpty() { List PtrL; PtrL = (List)malloc(sizeof(st
数据结构学习笔记——线性表
lmma1的博客
07-15 545
已知一个结点，只能对后继结点进行操作（插入/删除)——单链表不能删除当前结点！（2）循环链表尾指针是头指针的前驱，对表头和表尾操作都是O(1).（3）循环链表尾指针指向的是头结点而不是第一个元素的结点！（1）顺序表插入删除要移动元素！（1）需要知道插入位置的前驱结点（从表头顺序遍历）（1）要知道删除结点的前驱结点（从表头顺序遍历）（2）先修改要插入的结点（新结点）的指针。（2）插入：先修改新结点，再修改前驱结点。（2）只需要修改前驱结点的指针。（3）删除：只需修改前驱结点。（3）再修改前驱结点的指针。
数据结构——学习笔记——入门必看【建议收藏】
热门推荐
刘鑫磊
02-09 49万+
（2）静态查找表&动态查找表的区别用法【顺序查找-线性查找-折半查找-二分查找-有序表查找-插值查找-斐波那契查找-索引顺序表查找-分块查找】单独使用顺序存储结构（即数组）无法很好地实现树的存储概念，不过如果充分利用顺序存储和链式存储结构的特点，则完全可以实现对数的存储结构的表示。深度为 2，则至多只有 3 个结点：根结点，根结点的左子树，根结点的右子树···指的是这样一个数列：1、1、2、3、5、8、13、21、……（3）四中常见的多路查找树【2-3 树$2-3-4 树$B 树$B+ 树】的区别用法。
数据结构学习笔记——线性表之顺序表
2402_84707567的博客
05-19 2021
5)取表中某个元素：GetList(L , i ), 即ai。3)判断表是否为空：list_empty (L)。定位：确定给定元素x在表L中第一次出现的位置（或序号）。即实现Locate(L,x)。若将线性表L=(a0,a1, ……,an-1)中的各元素依次存储于计算机一片。6)定位运算：Locate(L,x)设有一个顺序表L={1,2,3,4,5,6}1)建立一个空表：list_create(L)2)置空表：list_clear(L)。使用二元组描述L=(D,R),则。4)求表长：length (L)
【数据结构】学习笔记之线性表
大雨的博客
10-13 747
​线性表中数据元素之间的关系是一对一的关系，即除了第一个和最后一个数据元素之外，其它数据元素都是首尾相接的（注意，这句话只适用大部分线性表，而不是全部。比如，循环链表逻辑层次上也是一种线性表（存储层次上属于链式存储，但是把最后一个数据元素的尾指针指向了首位结点））。
数据结构与算法学习笔记
ityqing的博客
09-25 35万+
本文是王争老师的《算法与数据结构之美》的学习笔记，详细内容请看王争的专栏。有不懂的地方指出来，我做修改。 数据结构与算法思维导图 数据结构指的是“一组数据的存储结构”，算法指的是“操作数据的一组方法”。 数据结构是为算法服务的，算法是要作用再特定的数据结构上的。 最常用的数据结构预算法: 数据结构：数组、链表、栈、队列、散列表、二叉树‘、堆、跳表、图、Tire树 算法： 递归...
数据结构学习笔记：线性表
RG_Aurora的博客
08-06 458
线性表（List）：零个或多个数据元素的有限序列。线性表类似于数学中的数列，只不过是有限的，因此可将线性表记为a1ai−1aiai1ana1​...ai−1​ai​ai1​...an​，称ai−1a_{i-1}ai−1​是aia_iai​的直接前驱元素ai1a_{i+1}ai1​是aia_iai​的直接后继元素，于是当i12n−1i12...n−1时，ai。
数据结构笔记二——线性表
weixin_64908198的博客
04-12 2029
线性表
数据结构学习笔记——线性表逻辑结构和顺序存储结构
weixin_62440328的博客
10-26 2600
用顺序存储方法存储的线性表。所谓顺序存储方法存储的线性表就是把线性表的结点按逻辑次序依次存放在一组地址连续的存储单元里的方法。
【学习笔记】数据结构 第二章 线性表
qq_61951986的博客
07-17 1873
静态存储分配，编译时确定容量 ，用一段地址连续的存储单元依次存储线性表的数据，逻辑关系通过存储位置来实现动态存储分配，运行时分配空间，用一组任意的存储单元存放线性表的数据元素，用指针来反应数据元素之间的逻辑关系。2.插入和删除操作相对复杂，要移动大量元素。3.占用连续内存空间，大小固定，诺空间不足要扩容。4.适合元素数量固定 或 较少的场景如：静态数据 或 需要随机访问的情况。特点：1.元素在内存中不连续，每个节点除了存储的数据外还要存：指向下一个节点的指针。
数据结构学习笔记
2402_83192253的博客
04-01 2343
数据结构：数据的逻辑结构、存储结构及操作。
数据结构_张铭教材_线性表_学习笔记与习题解析_1741870214.zip
03-16
本学习笔记与习题解析主要围绕线性表这一数据结构展开，详细介绍了线性表的概念、特点及其在程序设计中的应用。线性表是最基本、最简单的一种数据结构，其数据元素之间是一对一的关系，具有相同的特性，且数据元素的...
数据结构学习笔记：线性表、树与图的详解
结合描述“大学生 C/C++/JAVA/Python数据结构学习笔记和资料大全”，可以判断这是一套系统化、语言通用性强的学习资源，适合初学者打牢基础，也便于进阶者查漏补缺。 首先来看**线性表**。线性表是一种最基础的数据...
数据结构04——二叉树搜索树BST
moranxiao199的博客
12-16 494
Find查找的效率取决于树的高度，所以我们希望这个树尽量的平衡，不要出现一边倒。支持：查找（Search）、插入（Insert）、删除（Delete）第三种，删除的结点有左、右两颗子树：用另一个结点代替被删除的结点，同一组元素，如果插入顺序不同，二叉搜索树的形态可以完全不同。② 如果 X 大于根结点的关键值，在右子树中进行继续搜索；③ 若两者比较结果相等，搜索完成，返回指向此结点的指针。查找从根结点开始，如果树为空，返回 NULL。：将其父结点的指针指向被删除结点的孩子结点。
数据结构：矩阵
闲余知道
12-16 866
数据结构：矩阵
八大排序之：冒泡排序、快速排序和堆排序
t2786024916的博客
12-16 791
冒泡排序（Bubble Sort）是一种简单的排序算法，它重复地遍历要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。这个算法的名称由来是因为越小的元素会经由交换慢慢"浮"到数列的顶端（升序排列）。
数据结构入门：二叉排序树的删除算法
最新发布
2403_89732016的博客
12-18 447
有序二叉树（二叉搜索树）的核心特性是，删除节点时需要保证删除后树的有序性不被破坏。
数据结构-绪论
2401_87622134的博客
12-18 988
数据结构研究数据元素间的逻辑关系，包括集合、线性、树和图四种基本结构。存储结构是逻辑结构在计算机中的实现方式，分为顺序、链接、索引和散列四种模型。算法设计是解决问题的关键，常用策略有蛮力、分治、贪心和动态规划等。算法评价注重正确性、易读性、健壮性和效率，并通过复杂性分析评估其时间与空间开销。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值