JAVA-归并排序(图解)

一、基本思路

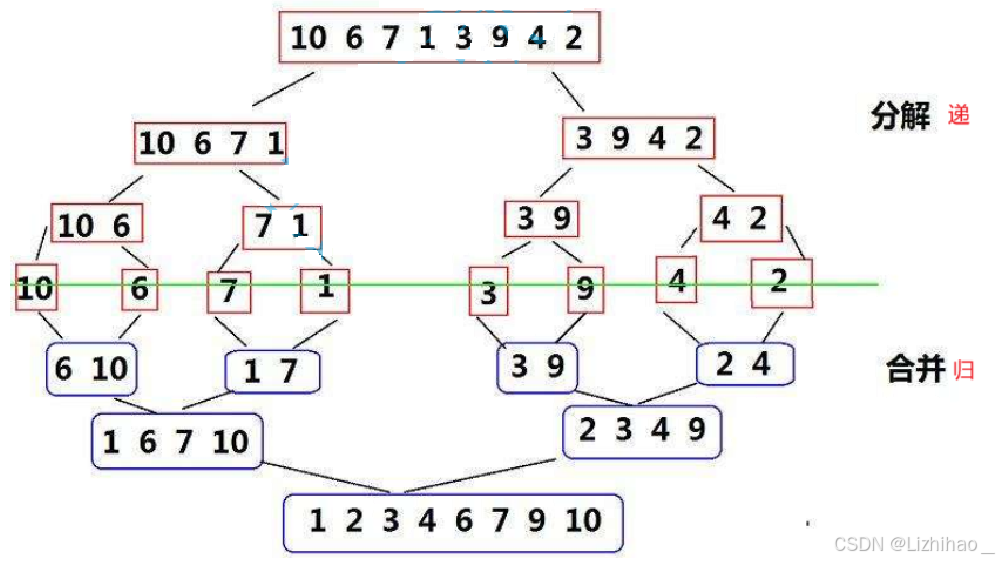
归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。 归并排序核心步骤：

归并排序拆分合并过程其实是递归实现的，所以我们要根据中间绿色的线，把这个图看为对折的图 ：

 二、归并排序的实现

1.拆解过程

 我们先来做分解（递）的过程：

 

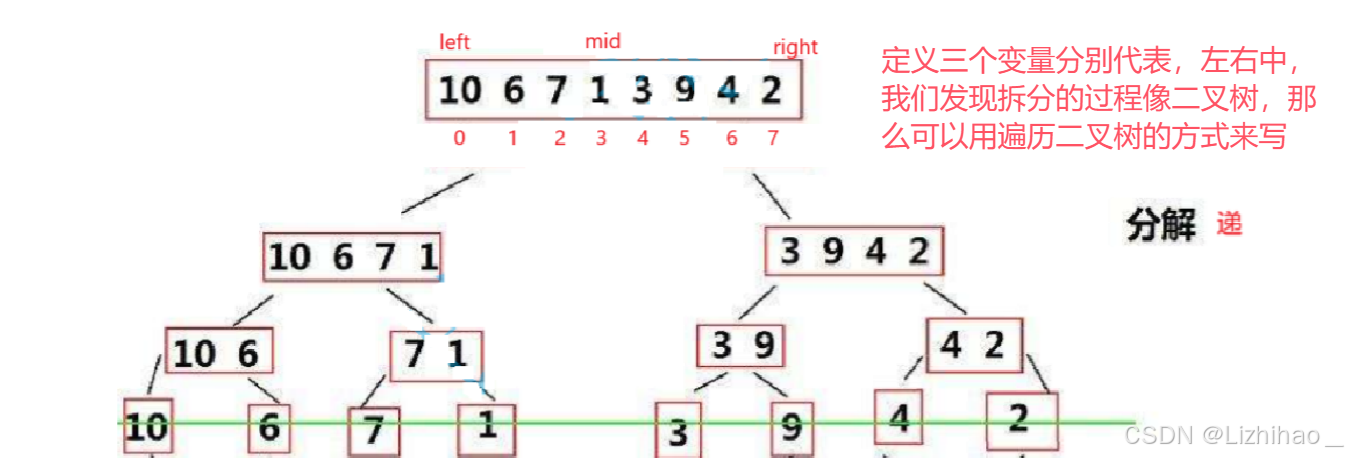
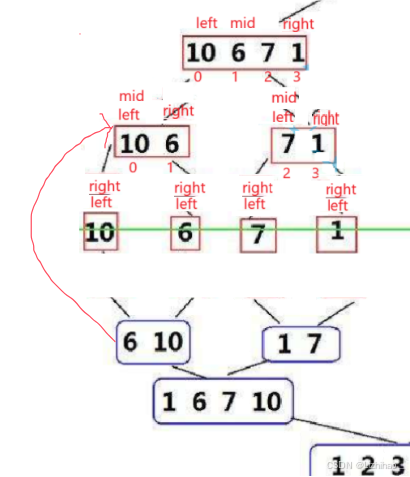
 观察发现

对于左子树，left还是在原来位置，right是原来mid的位置

对于右子树，left在mid+1位置，right还是原来位置

mid可以通过(left+right) / 2来获取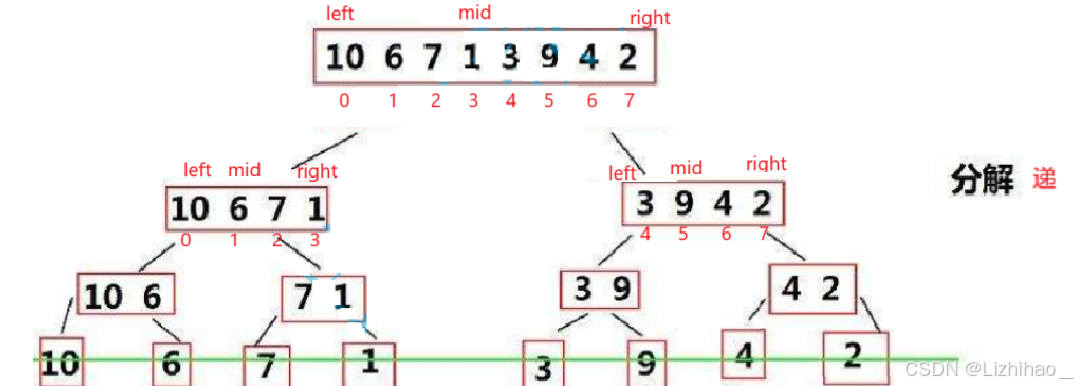  

那么我们现在可以写出这样的代码：

    public static void mergeSort(int[] array) {
        mergeSortFun(array,0,array.length-1);
    }

    private static void mergeSortFun(int[] array,int left,int right) {
    
        int mid = (left + right) / 2;

        //左
        mergeSortFun(array,left,mid);
        //右
        mergeSortFun(array,mid+1,right);

        //合并……
       

    }

 但是递归必须要有结束条件，那么我们需要按照这个思想继续往下执行，来观察结束条件：

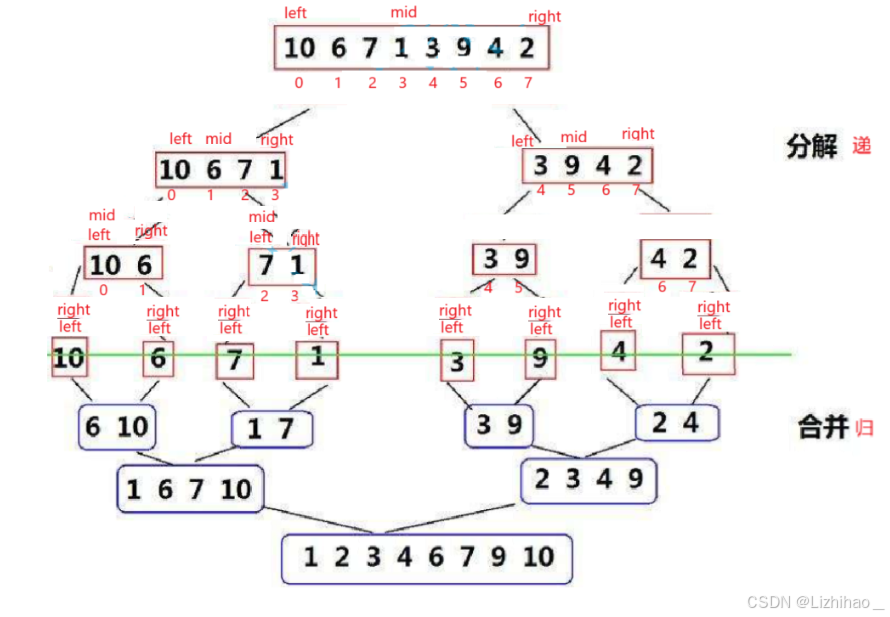
当为分解为一个元素的时候left和right会重合，为了能更好理解我再代入一个案例：

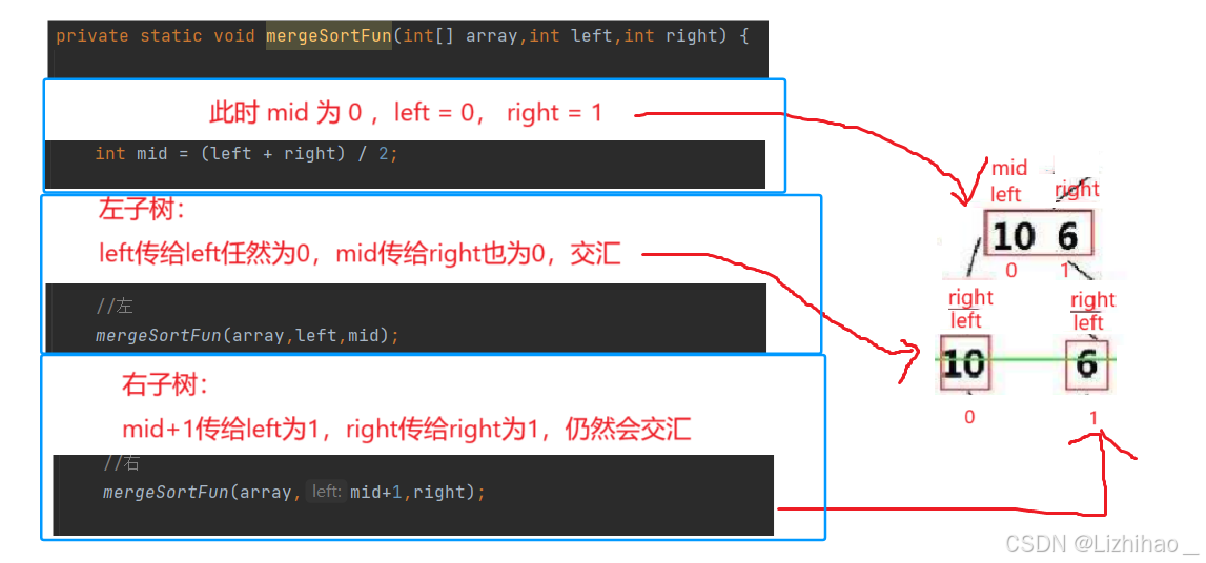
 那么我们就知道了结束条件：

    public static void mergeSort(int[] array) {
        mergeSortFun(array,0,array.length-1);
    }

    private static void mergeSortFun(int[] array,int left,int right) {
        //结束条件
        //为了预防会有超出的情况所以多写一个大于
        if (left >= right) {
            return;
        }
        int mid = (left + right) / 2;

        //左
        mergeSortFun(array,left,mid);
        //右
        mergeSortFun(array,mid+1,right);

        //合并……
    }

2.合并过程

再来做合并的过程 （归）

提醒：

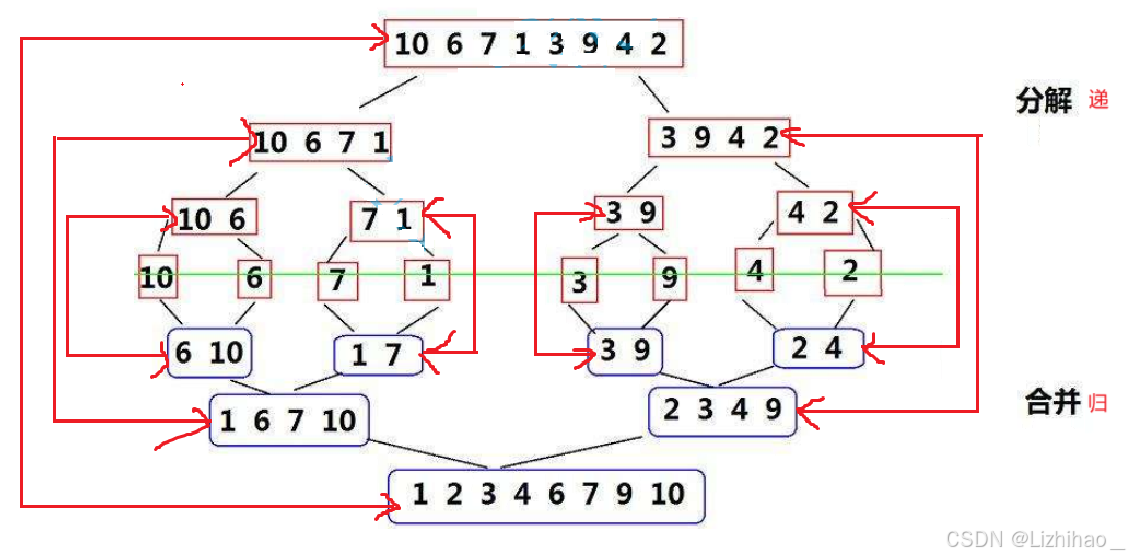
因为我们是归的过程，所以其实下面6 10排完序开辟的方法，其实就是上面10 6同一个开辟的空间。 

 

 合并思路：​​​​​​​

 

 

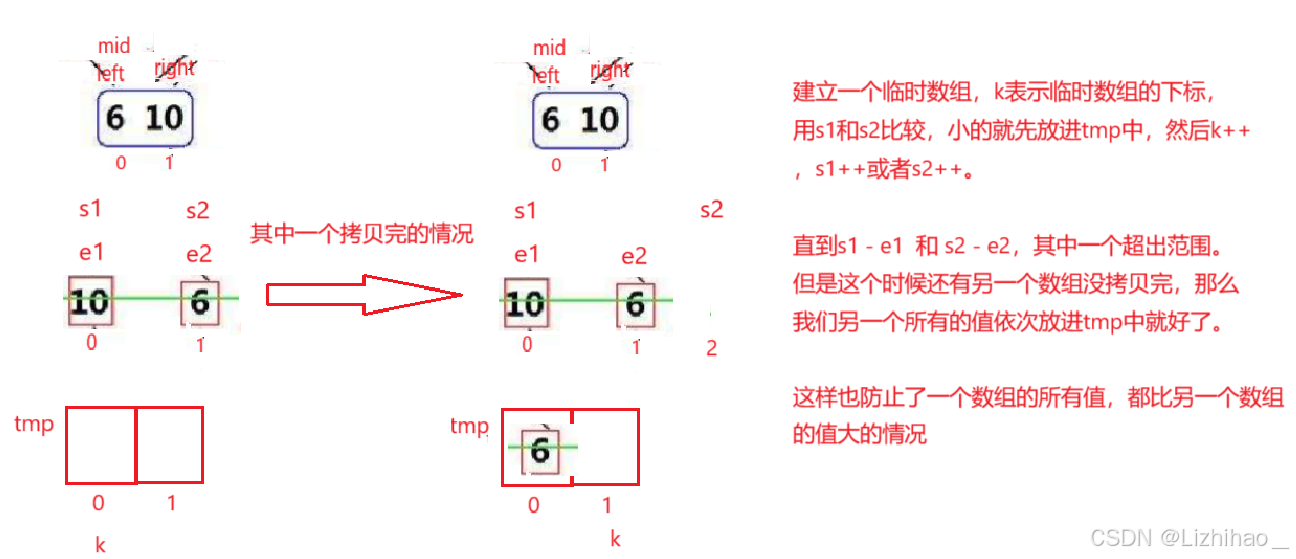
排序虽然完成了但是，这是在tmp临时数组中排的，还需要拷贝回源来的数组 ：

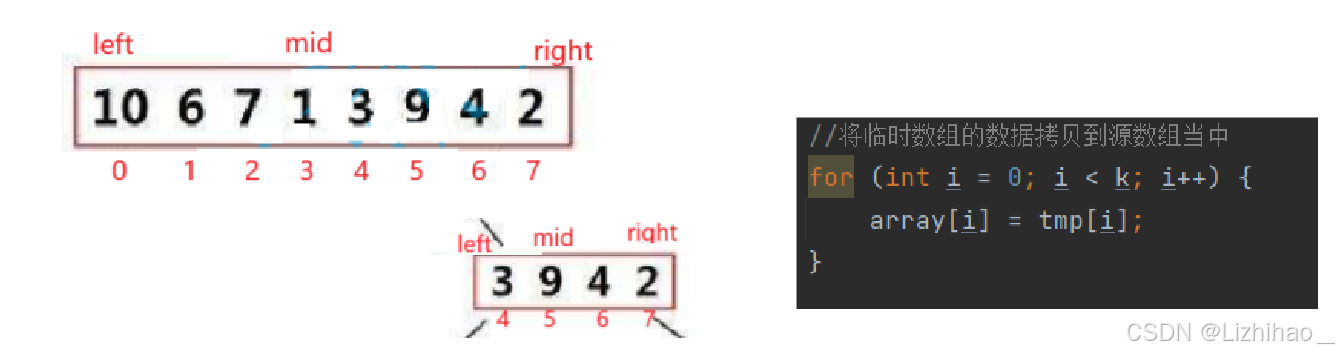
加上这样一段代码行吗，是不行的。不是所有情况都是从0下标开始

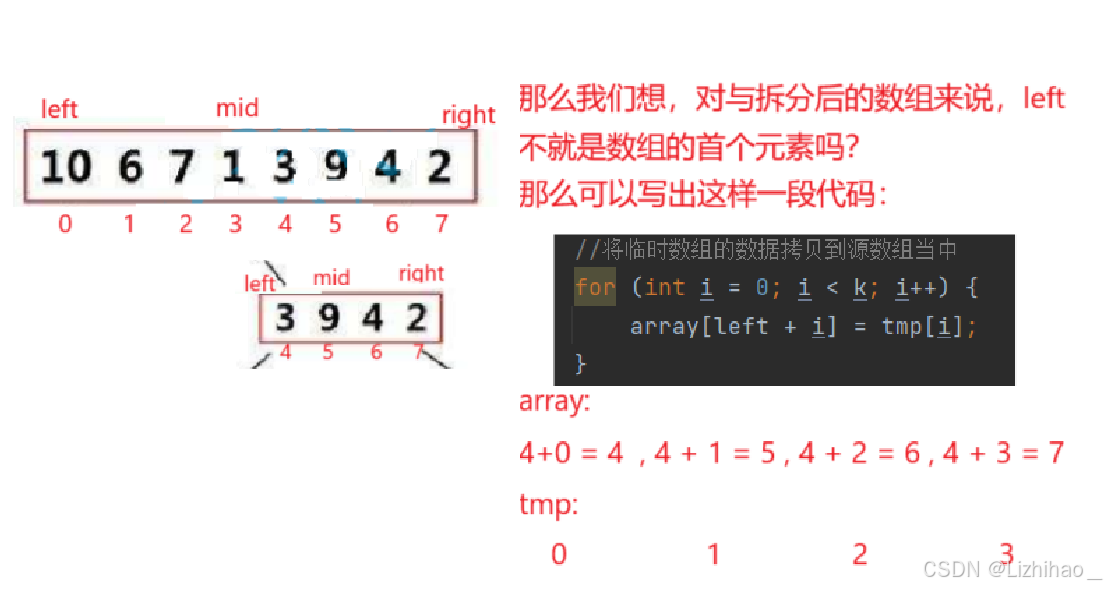这就是整套合并逻辑，由于单个元素合并比较特殊，我再将上述图的下一步合并画一下方便理解：

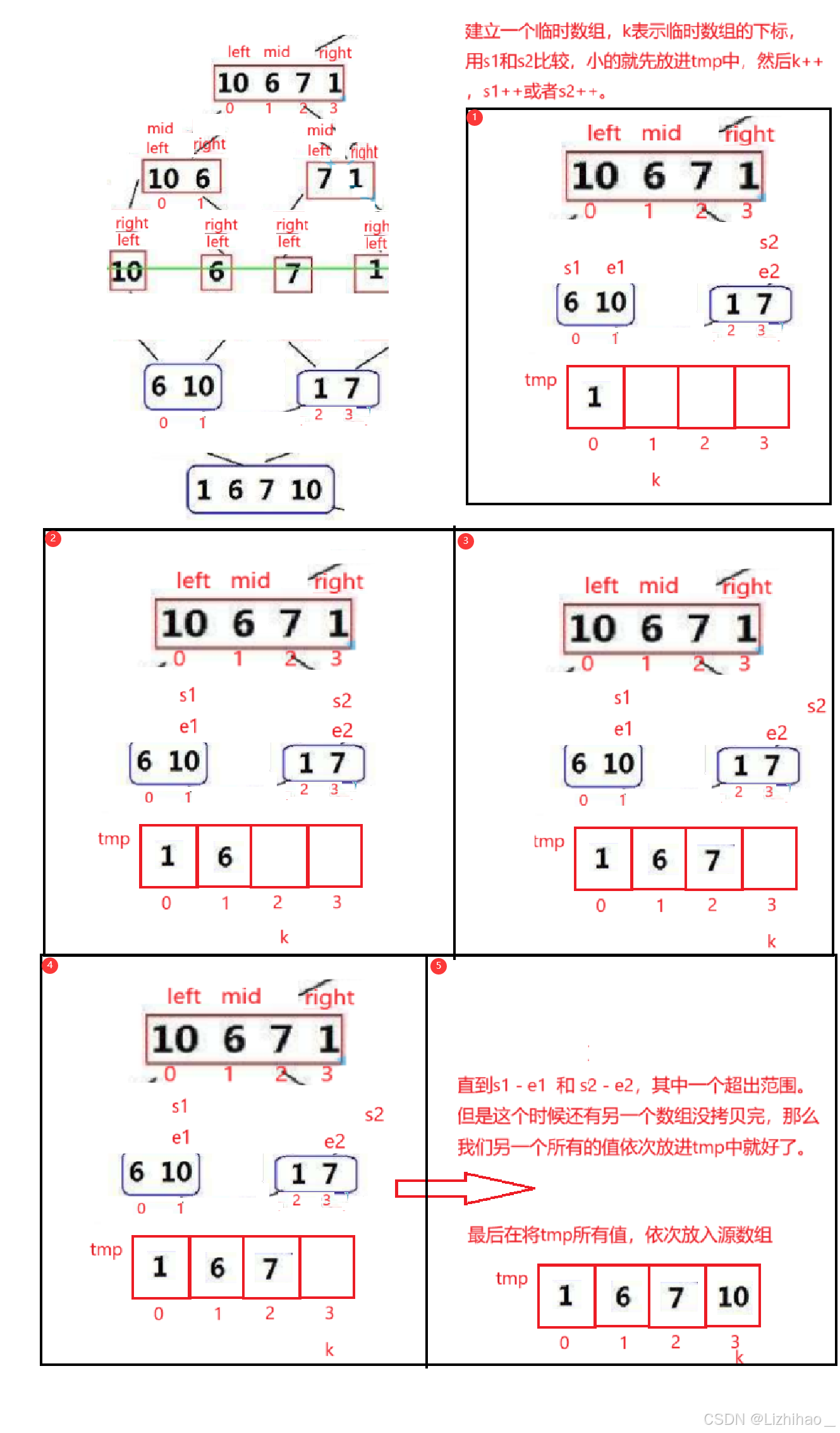
3.代码

    /**
     * 时间复杂度：0(N * log2N)
     * 空间复杂度：O(N)
     * 稳定性：稳定的排序
     * @param array
     */
    public static void mergeSort(int[] array) {
        mergeSortFun(array,0,array.length-1);
    }

    private static void mergeSortFun(int[] array,int left,int right) {
        //结束条件
        //为了预防会有超出的情况所以多写一个大于
        if (left >= right) {
            return;
        }
        int mid = (left + right) / 2;

        //左
        mergeSortFun(array,left,mid);
        //右
        mergeSortFun(array,mid+1,right);

        //合并
        merge(array,left,mid,right);

    }
    private static void merge(int[] array,int left,
                              int mid,int right) {
        //建立临时数组
        int[] tmp = new int[right - left + 1];
        //临时数组下标
        int k = 0;
        //第一组数据的范围
        int s1 = left;
        int e1 = mid;
        //第二组数据的范围
        int s2 = mid+1;
        int e2 = right;

        //while (s1 < e1 && s2 < e2) 不稳定的写法
        while (s1 <= e1 && s2 <= e2) {
            if(array[s1] <= array[s2]) {
                tmp[k] = array[s1];
                k++;
                s1++;
            }else {
                tmp[k] = array[s2];
                k++;
                s2++;
            }
        }

        //看哪一个数组没有拷贝完
        while (s1 <= e1) {
            tmp[k] = array[s1];
            k++;
            s1++;
        }
        while (s2 <= e2) {
            tmp[k] = array[s2];
            k++;
            s2++;
        }

        //将临时数组的数据拷贝到源数组当中
        for (int i = 0; i < k; i++) {
            array[left + i] = tmp[i];
        }
    }

4.非递归实现

    /**
     * 非递归实现归并排序
     * @param array
     */
    public static void mergeSortNor(int[] array) {
        int gap = 1;
        while (gap < array.length) {
            for (int i = 0; i < array.length; i = i + 2*gap) {
                int left = i;
                int mid = left+gap - 1;
                if(mid >= array.length) {
                    mid = array.length-1;
                }
                int right = mid+gap;
                if(right >= array.length) {
                    right = array.length-1;
                }
                merge(array,left,mid,right);
            }
            gap *= 2;
        }
    }