交叉熵“的来源”与基尼系数

交叉熵是非常重要的损失函数，也是应用最多的损失函数之一。下面来介绍交叉熵的来源
我们知道，当样本真实样本标签 y = 1 时，上面式子第二项就为 1，概率等式转化为：

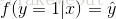
当真实样本标签 y = 0 时，上面式子第一项就为 1，概率等式转化为：

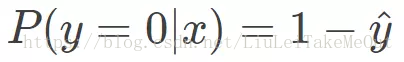
这时候，P(y|x)代表了这个模型预测正确的几率，我们当然希望的是概率 P(y|x) 越大越好，但是上面的指数特别烦人，按照以前数学的尿性，往往就是对其取对数将指数运算变成乘法，所以我们对 P(y|x) 引入 log 函数（底数要大于1）。则有：

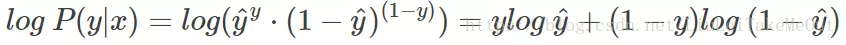
但是，损失函数表示模型的不准确的程度，不过没关系，只需要在式子的前面加上一个负号就能让其单调性改变，令 Loss = -log P(y|x) 即可。则得到损失函数为：

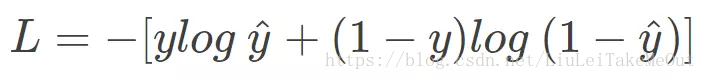
类推一下，假设y也是概率，不难得出交叉熵的计算公式

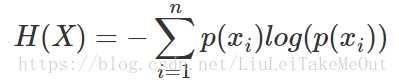
其实，这只是交叉熵与分类损失函数的联系。

换一个思路，假设一个事件，它发生的概率很小，但是还是发生了，这时候我们得找一个函数