一、引言
简单的说,树状数组是线段树的简化形式。
基于这种理解,在拿到一个长度为 999 的数组以后,十分自然得直接采用向下取整的办法,将长度为 999 的数组分割为长度分别为 444 和 555 的左右两个子区间。再反复进行上面的操作,直到区间长度无法再分。然后依据每层的区间关系,就可以得到一颗二叉树,而这棵二叉树正是区间树(如左图所示)。有了区间树以后,再去掉不必要的区间就获得了最后的树状数组。
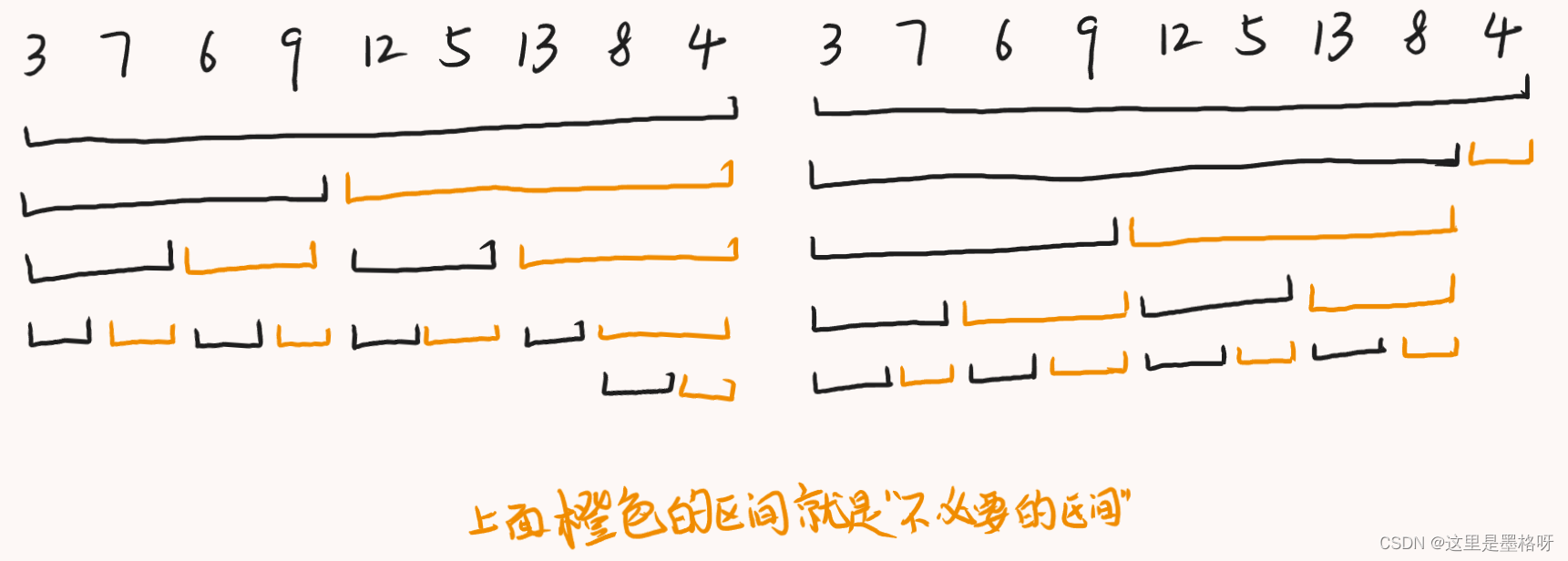
但是实际上,构建树状数组时通常不会采用这种分割方法,而用一种“补”的思想——将数组的长度补充为 222 的整数次方,然后再进行划分(如右图所示,其中未画出“补”的部分)。与此同时,引入了 lowbit 函数,以求出当前节点的父、子节点的索引号。
观察整个树状数组的推理过程,这种变化是十分突然的,数组长度为什么一定要补成 222 的整数次方?为什么 lowbit 函数能够建立起节点索引号与区间长度之间的关系?
为了进一步讨论这个问题,我首先做出了一个大胆的猜想,不使用 lowbit 函数能否实现树状数组?
二、一个猜想:“非常规”树状数组
当我们抛弃 lowbit 函数后,要面对的最大的问题就是,程序该如何寻找当前节点的父、子节点?一个可能的解决方案是将目标节点的父、子节点的索引号直接记录下来。于是可以设计下面这个类:
class Node{
public:
int value;
int parent;
int child;
Node(): value(-1), parent(-1), child(-1){
}
};
当我们能够寻找到目标节点的父子索引号以后,求区间和、单点修改等操作就与平常的树状数组的操作基本相同了。所以,这个“非常规数组”的关键在于如何 built 操作如何进行?
这时候,我们就要用上第一小节中所说的“树状数组是线段树的简化”的结论了。我们通过仿照线段树的构建过程,我们可以用一个递归算法构建整个树状数组。
三、222 的整数次方
区间长度定理
在构建非常规树状数组的时候,存在一种十分蹩脚的情况——奇数长度的数组。因为奇数没有办法被 222 整除,所以在向下二分的时候,总是要进行一定的取整操作。这就导致程序没有办法均匀地二分数组,总存在一些偏差。而当数组的长度为 222 的整数次方时,就不存在这种情况。更加有趣的是,这种数组二分建树后的任意一个区间都是 222 的整数次方!
我们定义第 111 层只有 111 个根区间,这是对原数组不进行任何二分操作的结果。第 222 层是对根区间进行一次二分后的结果,从左往右依次是第 111 个、第 222 个区间。接下来的层次都反复进行上面的操作,直到区间不可再分。最终就能够获得一棵树状数组。
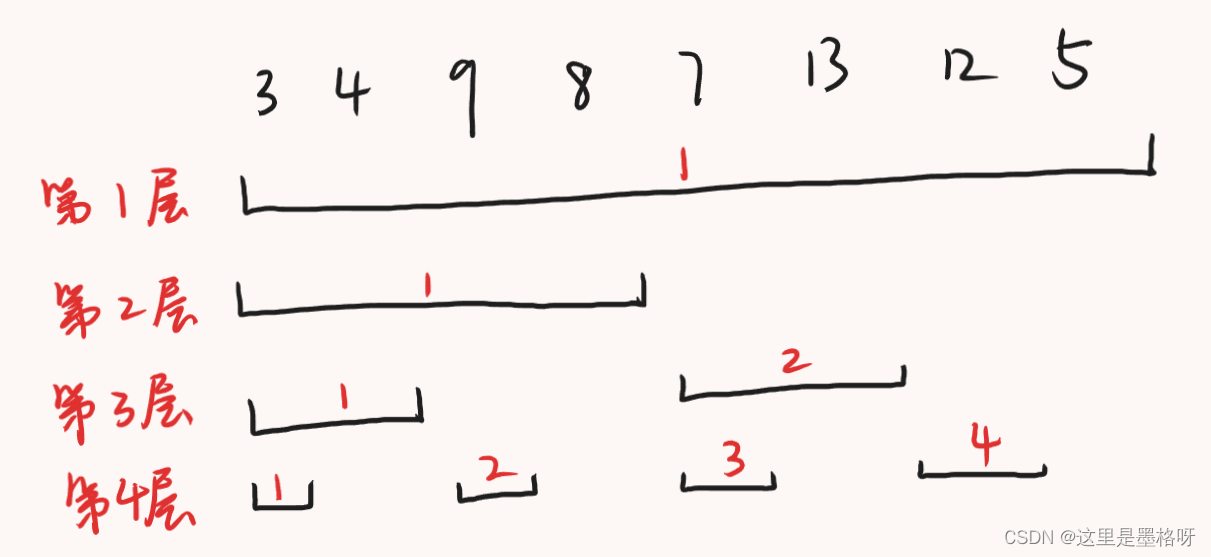
根据前面的推理,很容易发现,当数组的长度是 222 的整数次方时,每一层区间的长度都是相等的。又因为第一层的区间长度等于原数组的长度,所以,我们可以很容易得到任意层区间的长度。
区间长度定理:
已知数组长度 l=2n(n∈Z∗)l=2^n (n \in Z^*)l=2n(n∈Z





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2368
2368

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








