神经元(Neuron)
- 输入:x1,x2,x3x_1, x_2, x_3x1,x2,x3 是数据输入。
- 权重和偏置:每个输入与对应的权重 w1,w2,w3w_1, w_2, w_3w1,w2,w3 相乘,再加上偏置 bbb。
- 线性组合:计算加权和 z=∑i=1nxiwi+bz = \sum_{i=1}^n x_i w_i + bz=∑i=1nxiwi+b。
- 激活函数:将 zzz 通过激活函数 f(z)f(z)f(z) 映射为最终输出 aaa。
- 批量大小Batch:在神经网络中,一个神经元通常会处理多个数据输入,而不是只处理一个数据输入。(多个不同样本的同种特征数据)
- 神经元个数:在 输入层,神经元的个数通常等于输入数据的特征数,即每种特征对应一个神经元;在 隐藏层,神经元的个数通常是根据网络的复杂度和所需的表示能力来确定的。更多的神经元可以捕捉更复杂的特征关系,增强模型的表达能力。;在 输出层,神经元的个数通常与任务相关,例如,对于分类任务,输出层的神经元数可能与类别数相同;对于回归任务,输出层通常只有一个神经元。
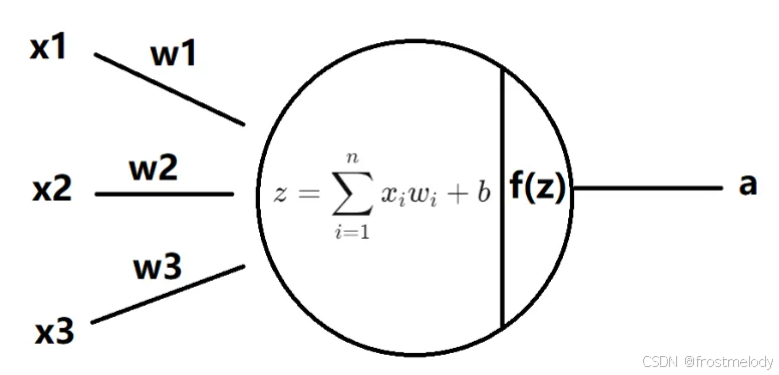
z=∑i=1nxiwi+b z = \sum_{i=1}^n x_i w_i + b z=i=1∑nxiwi+b
a=f(z) a = f(z) a=f(z)
激活函数(Activation function)
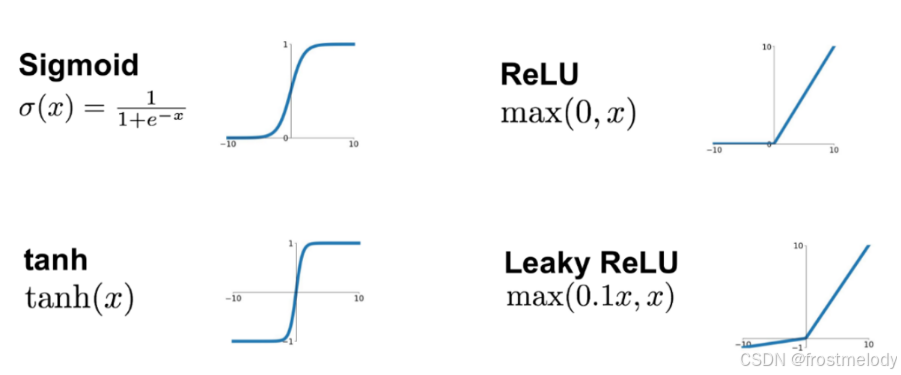
- Sigmoid
- 公式: σ(x)=11+e−x\sigma(x) = \frac{1}{1 + e^{-x}}σ(x)=1+e−x1
- 特点:
- 输出范围:(0,1)(0, 1)(0,1)
- 常用于二分类问题的输出层。
- 易受梯度消失问题影响(输入过大或过小时,梯度接近 0)。
- ReLU (Rectified Linear Unit)
- 公式: ReLU(x)=max(0,x)\text{ReLU}(x) = \max(0, x)ReLU(x)=max(0,x)
- 特点:
- 输出范围:[0,+∞)[0, +\infty)[0,+∞)
- 计算简单,加速训练。
- 解决了梯度消失问题,但可能导致“死神经元”(负值时梯度为 0)。
- tanh (双曲正切)
- 公式: tanh(x)=ex−e−xex+e−x\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}tanh(x)=ex+e−xex−e−x
- 特点:
- 输出范围:(−1,1)(-1, 1)(−1,1)
- 中心化(输出均值接近 0),有助于梯度稳定。
- 梯度消失问题较 Sigmoid 轻微,但仍存在。
- Leaky ReLU
- 公式: Leaky ReLU(x)=max(0.1x,x)\text{Leaky ReLU}(x) = \max(0.1x, x)Leaky ReLU(x)=max(0.1x,x)
- 特点:
- 输出范围:(−∞,+∞)(-\infty, +\infty)(−∞,+∞)
- 避免 ReLU 的“死神经元”问题,负值时有小斜率(如 0.1)。
- 提高模型鲁棒性,适合复杂任务。
把神经元组装成网络(Network)
- 隐藏层的神经元既不直接接收外部输入(不像输入层),也不直接输出结果给外部(不像输出层)。它在输入和输出之间起到一个“中间处理”的作用,因此被称为“隐藏层”。
- 一个神经网络的层数以及每一层中的神经元数量都是任意的
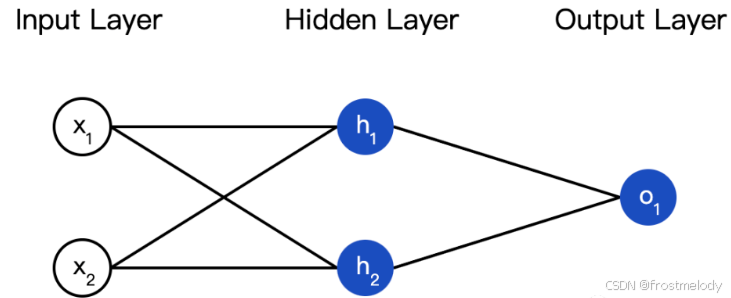
- 这个网络有两个输入,一个有两个神经元 (h1h_1h1 和 h2h_2h2) 的隐藏层,以及一个有一个神经元 (o1o_1o1) 的输出层。要注意,o1o_1o1 的输入就是 h1h_1h1 和 h2h_2h2 的输出,这样就组成了一个网络。
损失函数(Loss)
- 损失:真实值与网络预测值之间的误差
- 训练网络 = 最小化损失
- 如何才能逐步地减少损失? 通过调整网络的权重和截距项,可以改变其预测值
梯度下降(Gradient Descent)
- 是一种优化算法,用来最小化损失函数
- 它通过沿着损失函数关于权重参数的负梯度方向更新参数,使损失逐步变小
即w1←w1−η∂L∂w1w_1 \leftarrow w_1 - \eta \frac{\partial L}{\partial w_1}w1←w1−η∂w1∂L
η\etaη 是一个常数,被称为学习率,用于调整训练的速度。我们要做的就是用 w1w_1w1 减去η∂L∂w1\eta \frac{\partial L}{\partial w_1}η∂w1∂L
- 如果 ∂L∂w1\frac{\partial L}{\partial w_1}∂w1∂L 是正数,w1w_1w1 变小,LLL 会下降。
- 如果 ∂L∂w1\frac{\partial L}{\partial w_1}∂w1∂L 是负数,w1w_1w1 会变大,LLL 会上升。
如果我们对网络中的每个权重和截距项都这样进行优化,损失就会不断下降,网络性能会不断上升。
我们的训练过程是这样的:
- 从我们的数据集中选择一个样本,用随机梯度下降法进行优化——每次我们都只针对一个样本进行优化;
- 计算每个权重或截距项对损失的偏导(例如 ∂L∂w1\frac{\partial L}{\partial w_1}∂w1∂L、∂L∂w2\frac{\partial L}{\partial w_2}∂w2∂L 等);
- 用更新等式更新每个权重和截距项;
- 重复第一步;
代码:一个完整的神经网络(Neuron Network)
数据
网络结构
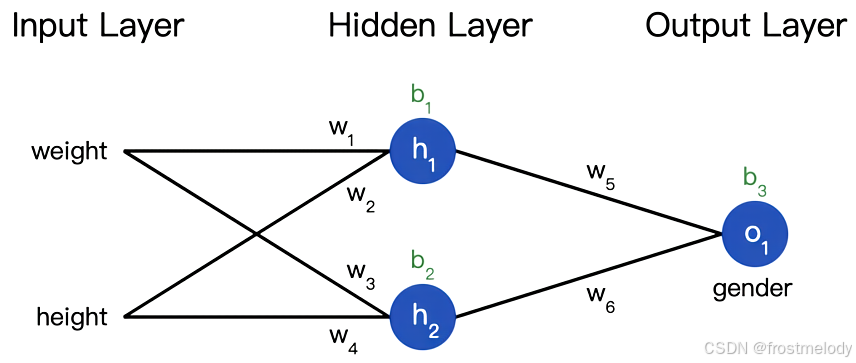
输入层到隐藏层:
h1=σ(w1⋅weight+w2⋅height+b1)
h_1 = \sigma\left(w_1 \cdot \text{weight} + w_2 \cdot \text{height} + b_1\right)
h1=σ(w1⋅weight+w2⋅height+b1)
h2=σ(w3⋅weight+w4⋅height+b2)
h_2 = \sigma\left(w_3 \cdot \text{weight} + w_4 \cdot \text{height} + b_2\right)
h2=σ(w3⋅weight+w4⋅height+b2)
隐藏层到输出层:
o1=σ(w5⋅h1+w6⋅h2+b3)
o_1 = \sigma\left(w_5 \cdot h_1 + w_6 \cdot h_2 + b_3\right)
o1=σ(w5⋅h1+w6⋅h2+b3)
其中:
- σ(⋅)\sigma(\cdot)σ(⋅) 表示激活函数(如 sigmoid 或 ReLU)。
- wiw_iwi 表示权重。
- bib_ibi 表示偏置。
完整代码
import numpy as np
def sigmoid(x):
# Sigmoid激活函数: f(x) = 1 / (1 + e^(-x))
# 将任意实数映射到(0,1)区间,常用于神经网络中
return 1 / (1 + np.exp(-x))
def deriv_sigmoid(x):
# Sigmoid函数的导数: f'(x) = f(x) * (1 - f(x))
# 在反向传播中用于计算梯度
fx = sigmoid(x)
return fx * (1 - fx)
def mse_loss(y_true, y_pred):
# 均方误差损失函数
# y_true和y_pred是相同长度的numpy数组
# 计算预测值与真实值差的平方的平均值
return ((y_true - y_pred) ** 2).mean()
class OurNeuralNetwork:
'''
一个简单的神经网络,包含:
- 2个输入节点
- 一个有2个神经元(h1, h2)的隐藏层
- 一个有1个神经元(o1)的输出层
这个网络可以解决简单的二分类问题
'''
def __init__(self):
# 初始化网络参数
# 权重初始化 - 使用正态分布随机初始化
# w1, w2: 连接输入层到第一个隐藏神经元h1的权重
self.w1 = np.random.normal()
self.w2 = np.random.normal()
# w3, w4: 连接输入层到第二个隐藏神经元h2的权重
self.w3 = np.random.normal()
self.w4 = np.random.normal()
# w5, w6: 连接隐藏层到输出神经元o1的权重
self.w5 = np.random.normal()
self.w6 = np.random.normal()
# 偏置项初始化 - 也使用正态分布随机初始化
# b1: 第一个隐藏神经元h1的偏置
self.b1 = np.random.normal()
# b2: 第二个隐藏神经元h2的偏置
self.b2 = np.random.normal()
# b3: 输出神经元o1的偏置
self.b3 = np.random.normal()
def feedforward(self, x):
'''
前向传播函数
参数x是一个包含2个元素的numpy数组,表示输入特征
返回网络的预测输出(一个0到1之间的值)
'''
# 计算隐藏层第一个神经元的输出
# h1 = sigmoid(w1*x1 + w2*x2 + b1)
h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1)
# 计算隐藏层第二个神经元的输出
# h2 = sigmoid(w3*x1 + w4*x2 + b2)
h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2)
# 计算输出层神经元的输出
# o1 = sigmoid(w5*h1 + w6*h2 + b3)
o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3)
return o1
def train(self, data, all_y_trues):
'''
训练神经网络
参数:
- data: 形状为(n x 2)的numpy数组,n为数据集中样本数量
- all_y_trues: 包含n个元素的numpy数组,对应data中每个样本的真实标签
'''
# 设置学习率 - 控制每次参数更新的步长
learn_rate = 0.1
# 设置训练轮数 - 整个数据集会被遍历的次数
epochs = 1000
# 开始训练过程
for epoch in range(epochs):
# 遍历数据集中的每个样本
for x, y_true in zip(data, all_y_trues):
# ------ 前向传播 ------
# 计算隐藏层神经元h1的输入和激活值
sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1
h1 = sigmoid(sum_h1)
# 计算隐藏层神经元h2的输入和激活值
sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2
h2 = sigmoid(sum_h2)
# 计算输出层神经元o1的输入和激活值(预测值)
sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3
o1 = sigmoid(sum_o1)
y_pred = o1
# ------ 反向传播计算梯度 ------
# 命名规则: d_L_d_w1 表示"损失L对权重w1的偏导数"
# 损失函数对预测值的偏导数: -2(y_true - y_pred)
d_L_d_ypred = -2 * (y_true - y_pred)
# 输出神经元o1的相关偏导数
# 预测值对w5的偏导数
d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1)
# 预测值对w6的偏导数
d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1)
# 预测值对b3的偏导数
d_ypred_d_b3 = deriv_sigmoid(sum_o1)
# 预测值对隐藏层神经元输出的偏导数
d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1)
d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1)
# 隐藏层神经元h1的相关偏导数
# h1对w1的偏导数
d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1)
# h1对w2的偏导数
d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1)
# h1对b1的偏导数
d_h1_d_b1 = deriv_sigmoid(sum_h1)
# 隐藏层神经元h2的相关偏导数
# h2对w3的偏导数
d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2)
# h2对w4的偏导数
d_h2_d_w4 = x[1] * deriv_sigmoid(sum_h2)
# h2对b2的偏导数
d_h2_d_b2 = deriv_sigmoid(sum_h2)
# ------ 使用梯度下降更新权重和偏置 ------
# 隐藏层神经元h1相关参数更新
# 应用链式法则计算复合函数的导数: dL/dw1 = dL/dy_pred * dy_pred/dh1 * dh1/dw1
self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1
self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2
self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1
# 隐藏层神经元h2相关参数更新
self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3
self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4
self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2
# 输出层神经元o1相关参数更新
# 对于输出层参数,链式法则更简单: dL/dw5 = dL/dy_pred * dy_pred/dw5
self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5
self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6
self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3
# ------ 每隔10个epoch计算并打印一次总损失 ------
if epoch % 10 == 0:
# 对所有样本进行预测
y_preds = np.apply_along_axis(self.feedforward, 1, data)
# 计算总损失
loss = mse_loss(all_y_trues, y_preds)
print("Epoch %d loss: %.3f" % (epoch, loss))
# 定义训练数据集
# 每个样本有两个特征,可以理解为计算机视角的[体重, 身高]等特征
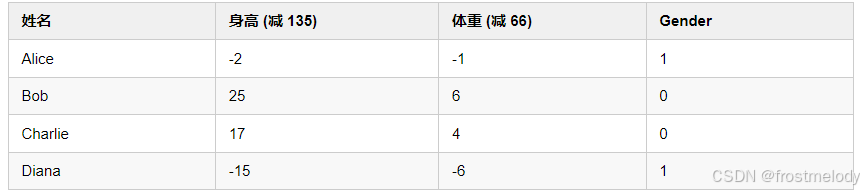
data = np.array([
[-2, -1], # Alice
[25, 6], # Bob
[17, 4], # Charlie
[-15, -6], # Diana
])
# 定义标签: 1表示女性, 0表示男性
all_y_trues = np.array([
1, # Alice - 女性
0, # Bob - 男性
0, # Charlie - 男性
1, # Diana - 女性
])
# 创建神经网络实例
network = OurNeuralNetwork()
# 训练神经网络
network.train(data, all_y_trues)
# 使用训练好的网络进行预测
# 预测两个新样本
emily = np.array([-7, -3]) # 特征类似于女性样本
frank = np.array([20, 2]) # 特征类似于男性样本
# 输出预测结果: 接近1表示预测为女性,接近0表示预测为男性
print("Emily: %.3f" % network.feedforward(emily)) # 预期输出接近1 - 女性
print("Frank: %.3f" % network.feedforward(frank)) # 预期输出接近0 - 男性
其他的一些适合纯小白的代码案例
CNN
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
def load_mnist(batch_size):
# 初始化MNIST数据集加载器的函数
# 超参数定义部分
# 输入图像的尺寸是28x28像素,因此输入尺寸为28
input_size = 28
# MNIST数据集包含10个不同的类别(数字0-9)
num_classes = 10
# 训练模型时将完整遍历数据集的次数设为3次
num_epochs = 3
# 指定每个批次处理的数据量为64(这里直接使用函数参数batch_size更灵活)
# 注意:下面代码中实际使用的batch_size会以函数参数为准
# 加载MNIST训练集
# 参数说明:
# root: 数据存储的根目录
# train: 设为True表示加载训练数据集
# transform: 将图像数据转化为PyTorch的Tensor格式
# download: 如果数据不存在则自动下载
train_dataset = datasets.MNIST(
root="../data",
train=True,
transform=transforms.ToTensor(),
download=True,
)
# 加载MNIST测试集
# 参数与训练集相似,只是train设为False来加载测试数据
test_dataset = datasets.MNIST(
root="../data", train=False, transform=transforms.ToTensor()
)
# 使用DataLoader创建数据加载器,它会在训练时按批次提供数据
# shuffle=True表示在每次训练之前都会随机打乱数据顺序,有助于训练过程的稳定性和泛化能力
train_loader = torch.utils.data.DataLoader(
dataset=train_dataset, batch_size=batch_size, shuffle=True
)
# 同样为测试集创建数据加载器
test_loader = torch.utils.data.DataLoader(
dataset=test_dataset, batch_size=batch_size, shuffle=True
)
# 函数最后返回训练和测试数据加载器,方便后续模型训练和评估使用
return train_loader, test_loader
# 定义一个卷积神经网络(CNN)类,继承自nn.Module
class CNN(nn.Module):
def __init__(self):
super(CNN, self).__init__() # 调用父类的构造函数初始化
# 定义第一个卷积层块
self.conv1 = nn.Sequential( # Sequential表示顺序容器
nn.Conv2d(
in_channels=1, # 输入通道数,灰度图是1通道
out_channels=16, # 输出通道数(特征图数)为16
kernel_size=5, # 卷积核大小为5x5
stride=1, # 卷积步长为1
padding=2, # 填充为2,使输出与输入大小相同
), # 卷积后输出的特征图大小为 (16, 28, 28)
nn.ReLU(), # ReLU激活函数,使非线性
nn.MaxPool2d(
kernel_size=2
), # 最大池化,池化核大小为2x2,输出大小变为 (16, 14, 14)
)
# 定义第二个卷积层块
self.conv2 = nn.Sequential( # 输入特征图大小为 (16, 14, 14)
nn.Conv2d(
16, 32, 5, 1, 2
), # 输入通道16,输出通道32,卷积核5x5,步长1,填充2
nn.ReLU(), # ReLU激活函数
nn.Conv2d(32, 32, 5, 1, 2), # 再次卷积,保持输入输出通道数相同
nn.ReLU(), # ReLU激活函数
nn.MaxPool2d(2), # 最大池化,池化核2x2,输出大小变为 (32, 7, 7)
)
# 定义第三个卷积层模块:继续深化特征学习
self.conv3 = nn.Sequential(
# 上一层输出是32个特征图,每个大小为14x14像素
nn.Conv2d(
in_channels=32, # 接收来自上一层的32个特征图
out_channels=64, # 本层输出将增强到64个特征图,有助于捕捉更复杂的特征
kernel_size=5, # 使用5x5的卷积核探索局部特征
stride=1, # 步长为1,意味着卷积核在特征图上逐像素移动
padding=2, # 填充2个像素,保持输出特征图尺寸与输入相同,这里是(14, 14)
),
nn.ReLU(), # 应用ReLU激活函数,增加网络的非线性表达能力,激活输出特征
# 注意:此处未再进行池化操作,保持空间尺寸为(64, 14, 14),更多关注特征的丰富而非下采样
)
# 定义全连接层
self.out = nn.Linear(
64 * 7 * 7, 10
) # 全连接层,将64*7*7个节点连接到10个输出节点(类别数为10)
# 定义前向传播过程
def forward(self, x):
x = self.conv1(x) # 输入数据经过第一个卷积层块
x = self.conv2(x) # 然后经过第二个卷积层块
x = self.conv3(x) # 再经过第三个卷积层块
x = x.view(
x.size(0), -1
) # 将多维的特征图展平成一维向量,形状为 (batch_size, 64*7*7)
output = self.out(x) # 输入到全连接层,得到最终的输出
return output # 返回输出结果
def accuracy(predictions, labels):
"""
计算模型预测的准确率,即预测正确的样本数占总样本数的比例。
- predictions: 这是一个来自PyTorch的张量(tensor),包含了模型对每个样本的预测得分。每个样本对应一列,每列中的数值表示该样本属于各个类别的可能性大小。
- labels: 同样是PyTorch张量,但这里存储的是每个样本的真实类别标签。它的形状应与predictions相对应,确保一一匹配。
返回值说明:
- rights: 一个整数,代表预测正确的样本数量。通过比较预测类别和实际类别得到。
- total: 一个整数,表示总共有多少个样本参与了这次准确率的计算。
"""
# 使用torch.max找到predictions中每行的最大值及对应的索引,索引即为预测的类别
pred = torch.max(predictions.data, 1)[1]
# 将预测类别pred与实际类别labels进行元素级比较,eq函数会返回一个布尔型张量,True表示预测正确,False表示预测错误。
# 使用sum函数累计预测正确的数量(True被视为1,False被视为0)
rights = pred.eq(labels.data.view_as(pred)).sum()
# 返回预测正确的数量和总样本数
return rights, len(labels)
def train_model(
net, train_loader, test_loader, num_epochs, batch_size, learning_rate=0.001
):
"""
参数:
net (nn.Module): 待训练的神经网络
train_loader (DataLoader): 训练数据加载器
test_loader (DataLoader): 测试数据加载器
num_epochs (int): 训练轮数
batch_size (int): 每批数据大小
learning_rate (float): 学习率,默认值为0.001
"""
# 定义损失函数
criterion = nn.CrossEntropyLoss()
# 定义优化器,这里使用Adam优化算法
optimizer = optim.Adam(net.parameters(), lr=learning_rate)
# 开始训练循环
for epoch in range(num_epochs):
# 保存当前epoch的结果
train_rights = []
# 针对训练数据加载器中的每一个批进行循环
for batch_idx, (data, target) in enumerate(train_loader):
net.train() # 将模型设置为训练模式
output = net(data) # 前向传播,获取模型输出
loss = criterion(output, target) # 计算损失
optimizer.zero_grad() # 清空梯度
loss.backward() # 反向传播,计算梯度
optimizer.step() # 更新参数
right = accuracy(output, target) # 计算准确率
train_rights.append(right) # 保存每批的准确率
# 每经过100个批次,进行一次验证
if batch_idx % 100 == 0:
net.eval() # 将模型设置为评估模式
val_rights = [] # 保存验证结果
# 针对验证数据加载器中的每一个批进行循环
for data, target in test_loader:
output = net(data) # 前向传播,获取模型输出
right = accuracy(output, target) # 计算准确率
val_rights.append(right) # 保存每批的准确率
# 计算训练集和验证集的准确率
# 计算训练集和验证集的总正确预测数以及总样本数
# 对于每个批次,train_rights和val_rights列表分别存储了该批次的正确预测数和总样本数
# tup[0]表示正确预测数,tup[1]表示总样本数
train_total_correct = sum(
[tup[0] for tup in train_rights]
) # 训练集总正确预测数
train_total_samples = sum(
[tup[1] for tup in train_rights]
) # 训练集总样本数
val_total_correct = sum(
[tup[0] for tup in val_rights]
) # 验证集总正确预测数
val_total_samples = sum(
[tup[1] for tup in val_rights]
) # 验证集总样本数
# 使用元组存储这些值,方便后续计算准确率
train_r = (train_total_correct, train_total_samples)
val_r = (val_total_correct, val_total_samples)
# 打印当前训练进度和性能指标,帮助初学者直观了解训练情况
# epoch: 当前正在进行的训练轮次
# [batch_idx * batch_size/{len(train_loader.dataset)}: 表示已完成的样本数/总样本数
# ({:.0f}%): 完成百分比,计算已完成的批次占总批次的比例
# 损失: {:.6f}: 当前批次的平均损失值,衡量模型预测错误的程度
# 训练集准确率: {:.2f}%: 根据train_r计算得出,表示训练集上模型预测正确的百分比
# 测试集正确率: {:.2f}%: 根据val_r计算得出,表示验证集上模型预测正确的百分比
print(
"当前epoch: {} [{}/{} ({:.0f}%)]\t损失: {:.6f}\t训练集准确率: {:.2f}%\t测试集正确率: {:.2f}%".format(
epoch, # 当前训练轮数
batch_idx * batch_size, # 当前批次结束时已处理的样本数
len(train_loader.dataset), # 总样本数
100.0 * batch_idx / len(train_loader), # 完成的百分比
loss.data, # 当前批次的损失值
100.0 * train_r[0] / train_r[1], # 训练集准确率
100.0 * val_r[0] / val_r[1], # 验证集准确率
)
)
if __name__ == "__main__":
# 加载MNIST数据集,每个批次64个样本
train_loader, test_loader = load_mnist(batch_size=64)
# 实例化一个卷积神经网络模型
net = CNN()
# 调用函数训练模型,传入网络模型、训练数据加载器、验证数据加载器、训练轮数和批次大小
train_model(net, train_loader, test_loader, num_epochs=2, batch_size=64)
simpleclassifier
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
def load_mnist(batch_size):
# 初始化MNIST数据集加载器的函数
# 超参数定义部分
# 输入图像的尺寸是28x28像素,因此输入尺寸为28
input_size = 28
# MNIST数据集包含10个不同的类别(数字0-9)
num_classes = 10
# 训练模型时将完整遍历数据集的次数设为3次
num_epochs = 3
# 指定每个批次处理的数据量为64(这里直接使用函数参数batch_size更灵活)
# 注意:下面代码中实际使用的batch_size会以函数参数为准
# 加载MNIST训练集
# 参数说明:
# root: 数据存储的根目录
# train: 设为True表示加载训练数据集
# transform: 将图像数据转化为PyTorch的Tensor格式
# download: 如果数据不存在则自动下载
train_dataset = datasets.MNIST(
root="../data",
train=True,
transform=transforms.ToTensor(),
download=True,
)
# 加载MNIST测试集
# 参数与训练集相似,只是train设为False来加载测试数据
test_dataset = datasets.MNIST(
root="../data", train=False, transform=transforms.ToTensor()
)
# 使用DataLoader创建数据加载器,它会在训练时按批次提供数据
# shuffle=True表示在每次训练之前都会随机打乱数据顺序,有助于训练过程的稳定性和泛化能力
train_loader = torch.utils.data.DataLoader(
dataset=train_dataset, batch_size=batch_size, shuffle=True
)
# 同样为测试集创建数据加载器
test_loader = torch.utils.data.DataLoader(
dataset=test_dataset, batch_size=batch_size, shuffle=True
)
# 函数最后返回训练和测试数据加载器,方便后续模型训练和评估使用
return train_loader, test_loader
# 定义一个卷积神经网络(CNN)类,继承自nn.Module
class CNN(nn.Module):
def __init__(self):
super(CNN, self).__init__() # 调用父类的构造函数初始化
# 定义第一个卷积层块
self.conv1 = nn.Sequential( # Sequential表示顺序容器
nn.Conv2d(
in_channels=1, # 输入通道数,灰度图是1通道
out_channels=16, # 输出通道数(特征图数)为16
kernel_size=5, # 卷积核大小为5x5
stride=1, # 卷积步长为1
padding=2, # 填充为2,使输出与输入大小相同
), # 卷积后输出的特征图大小为 (16, 28, 28)
nn.ReLU(), # ReLU激活函数,使非线性
nn.MaxPool2d(
kernel_size=2
), # 最大池化,池化核大小为2x2,输出大小变为 (16, 14, 14)
)
# 定义第二个卷积层块
self.conv2 = nn.Sequential( # 输入特征图大小为 (16, 14, 14)
nn.Conv2d(
16, 32, 5, 1, 2
), # 输入通道16,输出通道32,卷积核5x5,步长1,填充2
nn.ReLU(), # ReLU激活函数
nn.Conv2d(32, 32, 5, 1, 2), # 再次卷积,保持输入输出通道数相同
nn.ReLU(), # ReLU激活函数
nn.MaxPool2d(2), # 最大池化,池化核2x2,输出大小变为 (32, 7, 7)
)
# 定义第三个卷积层模块:继续深化特征学习
self.conv3 = nn.Sequential(
# 上一层输出是32个特征图,每个大小为14x14像素
nn.Conv2d(
in_channels=32, # 接收来自上一层的32个特征图
out_channels=64, # 本层输出将增强到64个特征图,有助于捕捉更复杂的特征
kernel_size=5, # 使用5x5的卷积核探索局部特征
stride=1, # 步长为1,意味着卷积核在特征图上逐像素移动
padding=2, # 填充2个像素,保持输出特征图尺寸与输入相同,这里是(14, 14)
),
nn.ReLU(), # 应用ReLU激活函数,增加网络的非线性表达能力,激活输出特征
# 注意:此处未再进行池化操作,保持空间尺寸为(64, 14, 14),更多关注特征的丰富而非下采样
)
# 定义全连接层
self.out = nn.Linear(
64 * 7 * 7, 10
) # 全连接层,将64*7*7个节点连接到10个输出节点(类别数为10)
# 定义前向传播过程
def forward(self, x):
x = self.conv1(x) # 输入数据经过第一个卷积层块
x = self.conv2(x) # 然后经过第二个卷积层块
x = self.conv3(x) # 再经过第三个卷积层块
x = x.view(
x.size(0), -1
) # 将多维的特征图展平成一维向量,形状为 (batch_size, 64*7*7)
output = self.out(x) # 输入到全连接层,得到最终的输出
return output # 返回输出结果
def accuracy(predictions, labels):
"""
计算模型预测的准确率,即预测正确的样本数占总样本数的比例。
- predictions: 这是一个来自PyTorch的张量(tensor),包含了模型对每个样本的预测得分。每个样本对应一列,每列中的数值表示该样本属于各个类别的可能性大小。
- labels: 同样是PyTorch张量,但这里存储的是每个样本的真实类别标签。它的形状应与predictions相对应,确保一一匹配。
返回值说明:
- rights: 一个整数,代表预测正确的样本数量。通过比较预测类别和实际类别得到。
- total: 一个整数,表示总共有多少个样本参与了这次准确率的计算。
"""
# 使用torch.max找到predictions中每行的最大值及对应的索引,索引即为预测的类别
pred = torch.max(predictions.data, 1)[1]
# 将预测类别pred与实际类别labels进行元素级比较,eq函数会返回一个布尔型张量,True表示预测正确,False表示预测错误。
# 使用sum函数累计预测正确的数量(True被视为1,False被视为0)
rights = pred.eq(labels.data.view_as(pred)).sum()
# 返回预测正确的数量和总样本数
return rights, len(labels)
def train_model(
net, train_loader, test_loader, num_epochs, batch_size, learning_rate=0.001
):
"""
参数:
net (nn.Module): 待训练的神经网络
train_loader (DataLoader): 训练数据加载器
test_loader (DataLoader): 测试数据加载器
num_epochs (int): 训练轮数
batch_size (int): 每批数据大小
learning_rate (float): 学习率,默认值为0.001
"""
# 定义损失函数
criterion = nn.CrossEntropyLoss()
# 定义优化器,这里使用Adam优化算法
optimizer = optim.Adam(net.parameters(), lr=learning_rate)
# 开始训练循环
for epoch in range(num_epochs):
# 保存当前epoch的结果
train_rights = []
# 针对训练数据加载器中的每一个批进行循环
for batch_idx, (data, target) in enumerate(train_loader):
net.train() # 将模型设置为训练模式
output = net(data) # 前向传播,获取模型输出
loss = criterion(output, target) # 计算损失
optimizer.zero_grad() # 清空梯度
loss.backward() # 反向传播,计算梯度
optimizer.step() # 更新参数
right = accuracy(output, target) # 计算准确率
train_rights.append(right) # 保存每批的准确率
# 每经过100个批次,进行一次验证
if batch_idx % 100 == 0:
net.eval() # 将模型设置为评估模式
val_rights = [] # 保存验证结果
# 针对验证数据加载器中的每一个批进行循环
for data, target in test_loader:
output = net(data) # 前向传播,获取模型输出
right = accuracy(output, target) # 计算准确率
val_rights.append(right) # 保存每批的准确率
# 计算训练集和验证集的准确率
# 计算训练集和验证集的总正确预测数以及总样本数
# 对于每个批次,train_rights和val_rights列表分别存储了该批次的正确预测数和总样本数
# tup[0]表示正确预测数,tup[1]表示总样本数
train_total_correct = sum(
[tup[0] for tup in train_rights]
) # 训练集总正确预测数
train_total_samples = sum(
[tup[1] for tup in train_rights]
) # 训练集总样本数
val_total_correct = sum(
[tup[0] for tup in val_rights]
) # 验证集总正确预测数
val_total_samples = sum(
[tup[1] for tup in val_rights]
) # 验证集总样本数
# 使用元组存储这些值,方便后续计算准确率
train_r = (train_total_correct, train_total_samples)
val_r = (val_total_correct, val_total_samples)
# 打印当前训练进度和性能指标,帮助初学者直观了解训练情况
# epoch: 当前正在进行的训练轮次
# [batch_idx * batch_size/{len(train_loader.dataset)}: 表示已完成的样本数/总样本数
# ({:.0f}%): 完成百分比,计算已完成的批次占总批次的比例
# 损失: {:.6f}: 当前批次的平均损失值,衡量模型预测错误的程度
# 训练集准确率: {:.2f}%: 根据train_r计算得出,表示训练集上模型预测正确的百分比
# 测试集正确率: {:.2f}%: 根据val_r计算得出,表示验证集上模型预测正确的百分比
print(
"当前epoch: {} [{}/{} ({:.0f}%)]\t损失: {:.6f}\t训练集准确率: {:.2f}%\t测试集正确率: {:.2f}%".format(
epoch, # 当前训练轮数
batch_idx * batch_size, # 当前批次结束时已处理的样本数
len(train_loader.dataset), # 总样本数
100.0 * batch_idx / len(train_loader), # 完成的百分比
loss.data, # 当前批次的损失值
100.0 * train_r[0] / train_r[1], # 训练集准确率
100.0 * val_r[0] / val_r[1], # 验证集准确率
)
)
if __name__ == "__main__":
# 加载MNIST数据集,每个批次64个样本
train_loader, test_loader = load_mnist(batch_size=64)
# 实例化一个卷积神经网络模型
net = CNN()
# 调用函数训练模型,传入网络模型、训练数据加载器、验证数据加载器、训练轮数和批次大小
train_model(net, train_loader, test_loader, num_epochs=2, batch_size=64)
decision_tree
from sklearn.tree import DecisionTreeClassifier, plot_tree
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import font_manager
font_path = "C:\\Windows\\Fonts\\simsun.ttc" # 替换为您系统中的中文字体路径
font_prop = font_manager.FontProperties(fname=font_path)
plt.rcParams["font.family"] = font_prop.get_name()
# 如果还需要更改字体的大小、样式等
plt.rcParams["font.size"] = 12 # 修改为您需要的大小
# 创建数据集
X = np.array(
[
[0, 2, 0], # 晴天,高温,无风
[1, 1, 1], # 阴天,中温,微风
[2, 0, 2], # 雨天,低温,强风
# ... 添加更多样本以增加模型的准确性
]
)
y = np.array([0, 1, 2]) # 分别对应去野餐、去博物馆、在家看书
# 初始化决策树模型,设置最大深度为5
clf = DecisionTreeClassifier(max_depth=5, random_state=42)
# 训练模型
clf.fit(X, y)
# 可视化决策树
plt.figure(figsize=(20, 10))
plot_tree(
clf,
filled=True,
feature_names=["天气状况", "温度", "风速"],
class_names=["去野餐", "去博物馆", "在家看书"],
rounded=True,
fontsize=12,
)
plt.show()
svm
from sklearn import datasets
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import font_manager
# 设置字体路径为系统中支持中文的字体
font_path = "C:\\Windows\\Fonts\\simsun.ttc" # 替换为您系统中的中文字体路径
font_prop = font_manager.FontProperties(fname=font_path)
plt.rcParams["font.family"] = font_prop.get_name()
from matplotlib import rcParams
# 或者直接指定负号字符为普通减号字符
rcParams["axes.unicode_minus"] = False
# 继续绘制图形代码
# 生成模拟数据
X, y = datasets.make_blobs(n_samples=50, centers=2, random_state=6)
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=42
)
# 创建 SVM 模型
model = SVC(kernel="linear")
model.fit(X_train, y_train)
# 绘制数据点和分类边界
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap="autumn")
# 绘制决策边界
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# 创建网格点
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = model.decision_function(xy).reshape(XX.shape)
# 绘制决策边界和间隔
ax.contour(
XX, YY, Z, colors="k", levels=[-1, 0, 1], alpha=0.5, linestyles=["--", "-", "--"]
)
plt.scatter(
model.support_vectors_[:, 0],
model.support_vectors_[:, 1],
s=100,
linewidth=1,
facecolors="none",
edgecolors="k",
)
plt.title("支持向量机分类示例")
plt.xlabel("特征1")
plt.ylabel("特征2")
plt.show()
randomforest
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
# 加载数据集
iris = load_iris()
X, y = iris.data, iris.target
# 训练随机森林模型
rf = RandomForestClassifier(n_estimators=3, random_state=42) # 使用3棵树以便于可视化
rf.fit(X, y)
# 绘制随机森林中的决策树
fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(20, 5), dpi=100)
for index in range(0, 3):
plot_tree(
rf.estimators_[index],
feature_names=iris.feature_names,
class_names=iris.target_names,
filled=True,
ax=axes[index],
)
axes[index].set_title(f"Tree {index + 1}")
plt.tight_layout()
plt.show()






















 731
731

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










