自服务数据分析：世界指数相关性、芝加哥交通违规与地理空间分析
本章深入探讨了高级自服务数据分析，通过创建世界指数相关性仪表板展示了如何从数据集中获取洞察并进行数据驱动的决策。首先检查数据质量，然后利用Tableau Prep Builder和Tableau Desktop创建参数化散点图以显示所有可能的相关性组合。接着，通过地理空间分析展示了芝加哥交通违规情况，进一步扩展了分析，引入距离度量。最后，通过添加折线趋势和颜色编码的热点图，展示了如何利用Tableau进行距离测量和地理空间分析。每个步骤都详细记录，以便于理解工作流程和决策过程。
This chapter focuses on advanced self-service analytics. Self-service analytics can be seen as a form of business intelligence, where people in a business are encouraged to execute queries on datasets themselves, instead of placing requests for queries in a backlog[ˈbæklɔːɡ]积压的工作 with an IT team. Then, query analysis can be done, which should lead to more insights and data-driven decision-making. But how do you start creating useful self-service dashboards if it's your first time doing so? How do you go from a dataset to a product? Have you ever asked yourself how other people start working on a dashboard, how they clean data, and how they come up with a dashboard design? If so, this is the right chapter for you! I want to share three use cases with you, written as a train of thought in order to give you an idea about how I work. Please note that this is just my personal experience; there are many different ways that can lead you to your goal.
We will cover the following topics:
- • Visualizing world indices correlations
- • Geo-spatial analytics地理空间分析 with Chicago traffic violations
- • Extending geo-spatial analytics with distance measures
Now that we have had this introduction, we are good to go and can start with the first use case.
Visualizing world indices correlations
Imagine you are working on the world indices dataset and your line manager(https://www.thebalancecareers.com/role-and-challenges-of-a-line-manager-2275752) gives you the following task:
Create a dashboard for me in which I can easily spot all correlated world indices and their distribution. I need it by tomorrow morning.
Now, take a few minutes before you continue reading and think about how you would tackle this task. The dataset contains 67 columns with various indices, like birth registrations or emission values, exports and imports, and forest areas, divided into 188 rows, where each row represents one country.
Write down your planned steps, open the workbook related to this chapter from https://public.tableau.com/profile/marleen.meier , and follow your steps; time it in order to get a better feel for time estimates when working with Tableau. This way, you can make sure that you can deliver on time and manage expectations if you are ever asked how long it will take to build a certain dashboard.
Plotting a scattergraph
- 1. First, I open the world-indices file in Tableau Prep Builder in order to get more details on the dataset itself; this will help us to describe the data but also to spot obvious data flaws like null values, duplicate entries, and so on:
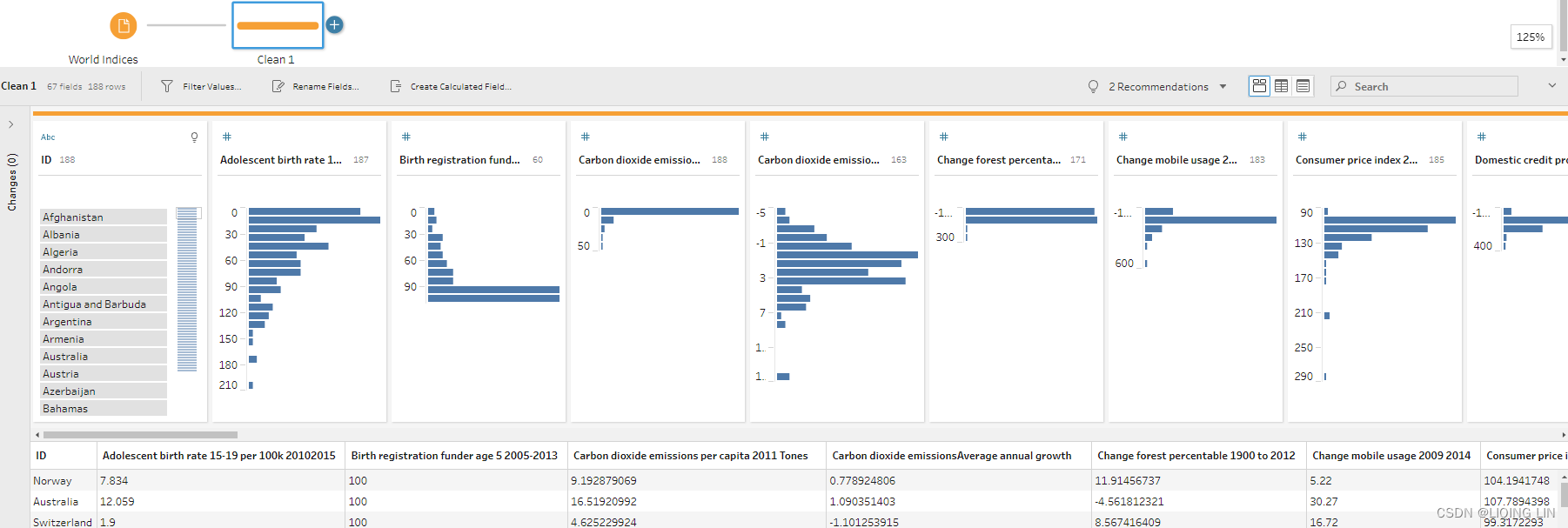
With this dataset, I actually didn't spot any obvious data quality issues in Prep Builder, nor a need to further prepare the data. It's 1 row per country—which you can see in the evenly distributed bars in the ID column—and 65 columns except Number of Records column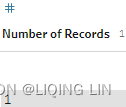
for the different indices per country(188 IDs and the records of other columns will not exceed 188 rows and each ID only has 1 Record ). Since no data preparation is needed, I decide to continue directly with Tableau Desktop. I close Tableau Prep Builder and open Tableau Desktop. - 2. My next thought is, how can I visualize all correlations at once, yet not have it be too much information? I do have 65 different columns, which makes for 4,225(=65*65) possible combinations.
(similar to https://blog.youkuaiyun.com/Linli522362242/article/details/111307026
)
No, I decide that displaying everything won't work. The task is very generic; therefore, I decide to go for a two-parameter approach, which will enable my end user to select each of the index combinations themselves. I start sketching what the dashboard might look like and come up with the following: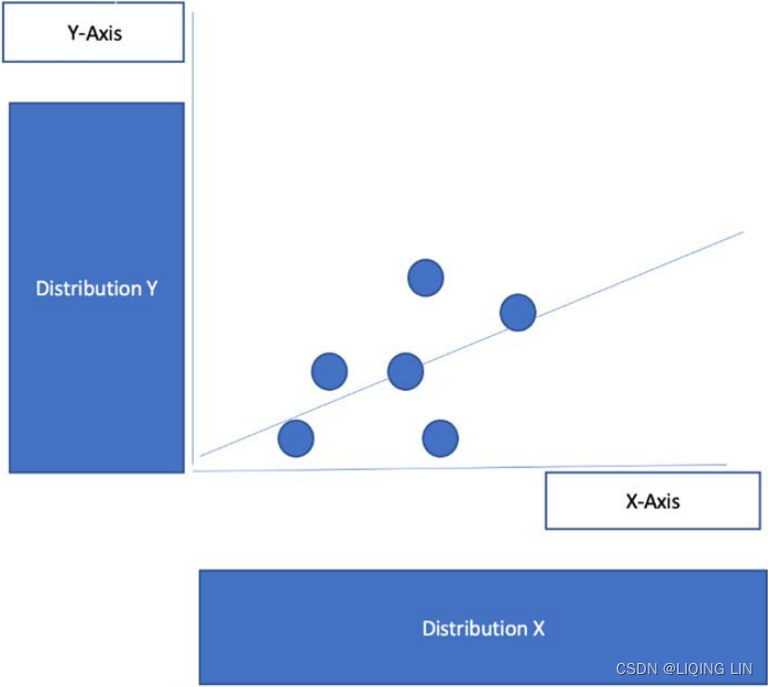
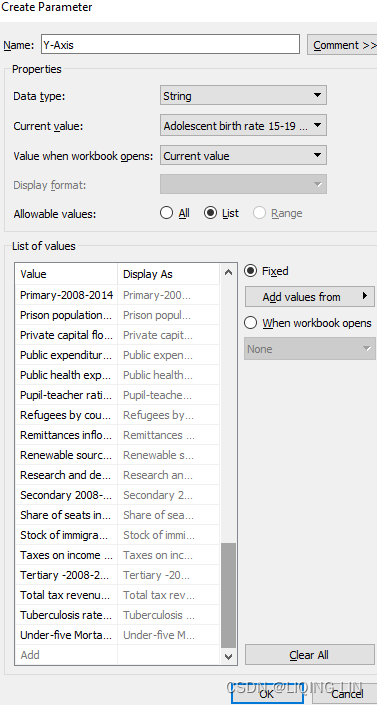
- 3. In order to execute my plan, I first create two parameters, which I name X-Axis and Y-Axis, which will be used to define the respective axes x and y.
- 4. I define both parameters as String and paste all field names from the clipboard into both of the parameters. To do this, I open the input file in Excel, transpose the header row to a column,
(https://support.microsoft.com/en-us/office/transpose-rotate-data-from-rows-to-columns-or-vice-versa-3419f2e3-beab-4318-aae5-d0f862209744copy the header row
and open an new excel file, then Right-click over the top-left cell of where you want to paste the transposed table in this new excel, and choose Transpose 
Next delete the ID row and Number of Records row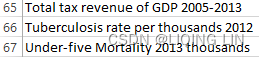
==>
.)
and press Ctrl + C.
The data can now be pasted into the parameter via the Paste from Clipboard option. This saves time and is less error-prone: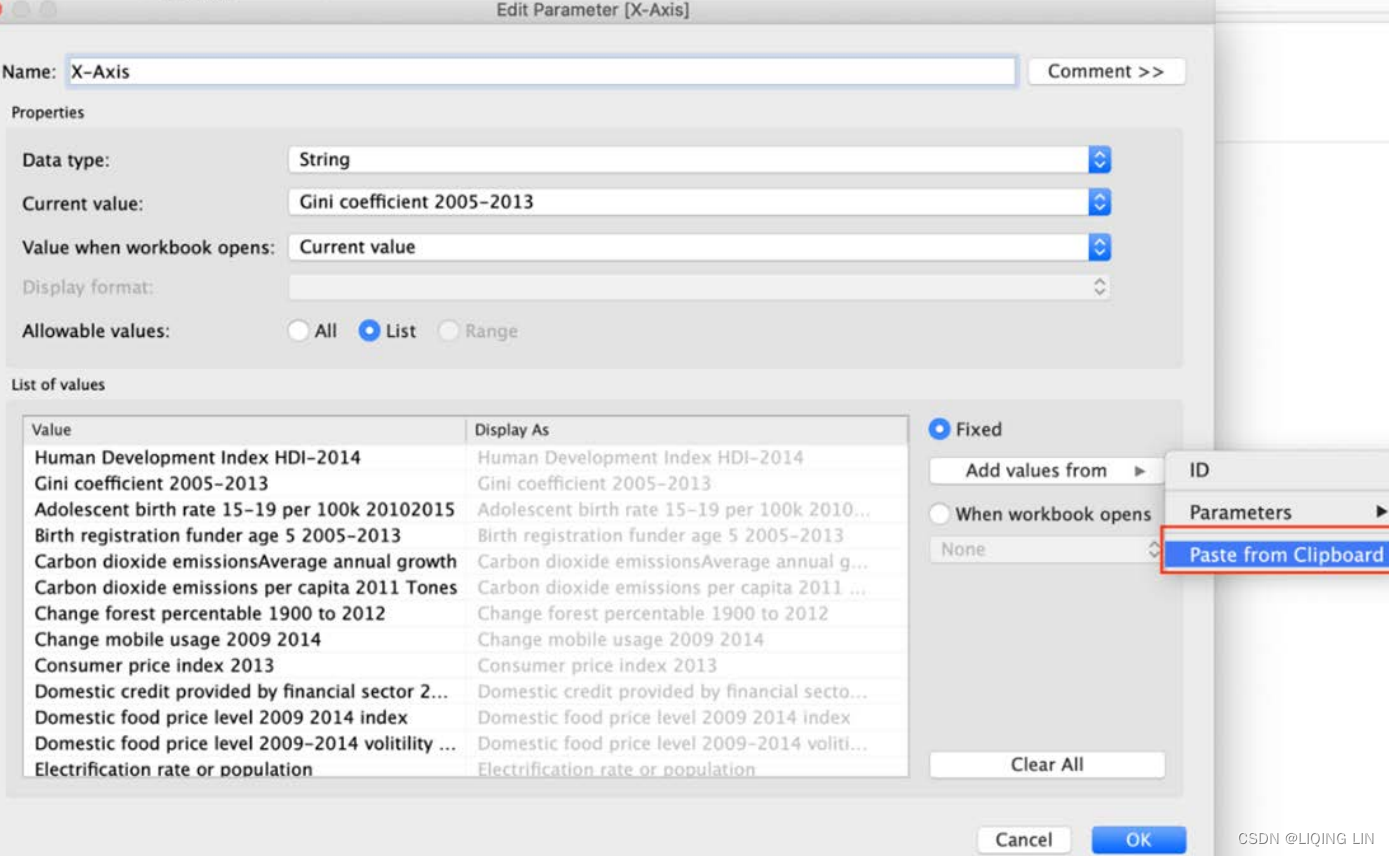
- 5. I also want the parameters to be visible on the dashboard, so I select Show Parameter:
- 6. If you were to test the parameter now, nothing would happen. We need a calculated field that defines that if a selection from the parameter has been made, Tableau will select the appropriate field. I create the following calculated field to achieve this (this field has been made part of the Starter and Solution workbook to make your life easier): X-Axis
If [Parameters].[X-Axis] = 'Human Development Index HDI-2014' then [Human Development Index HDI-2014] Elseif [Parameters].[X-Axis] = 'Gini coefficient 2005-2013' then [Gini coefficient 2005-2013] Elseif [Parameters].[X-Axis] = 'Adolescent birth rate 15-19 per 100k 20102015' then [Adolescent birth rate 15-19 per 100k 20102015] Elseif [Parameters].[X-Axis] = 'Birth registration funder age 5 2005-2013' then [Birth registration funder age 5 2005-2013] Elseif [Parameters].[X-Axis] = 'Carbon dioxide emissionsAverage annual growth' then [Carbon dioxide emissionsAverage annual growth] Elseif [Parameters].[X-Axis] = 'Carbon dioxide emissions per capita 2011 Tones' then [Carbon dioxide emissions per capita 2011 Tones] Elseif [Parameters].[X-Axis] = 'Change forest percentable 1900 to 2012' then [Change forest percentable 1900 to 2012] Elseif [Parameters].[X-Axis] = 'Change mobile usage 2009 2014' then [Change mobile usage 2009 2014] Elseif [Parameters].[X-Axis] = 'Consumer price index 2013' then [Consumer price index 2013] Elseif [Parameters].[X-Axis] = 'Domestic credit provided by financial sector 2013' then [Domestic credit provided by financial sector 2013] Elseif [Parameters].[X-Axis] = 'Domestic food price level 2009 2014 index' then [Domestic food price level 2009 2014 index] Elseif [Parameters].[X-Axis] = 'Domestic food price level 2009-2014 volitility index' then [Domestic food price level 2009-2014 volitility index] Elseif [Parameters].[X-Axis] = 'Electrification rate or population' then [Electrification rate or population] Elseif [Parameters].[X-Axis] = 'Expected years of schooling - Years' then [Expected years of schooling - Years] Elseif [Parameters].[X-Axis] = 'Exports and imports percentage GPD 2013' then [Exports and imports percentage GPD 2013] Elseif [Parameters].[X-Axis] = 'Female Suicide Rate 100k people' then [Female Suicide Rate 100k people] Elseif [Parameters].[X-Axis] = 'Foreign direct investment net inflows percentage GDP 2013' then [Foreign direct investment net inflows percentage GDP 2013] Elseif [Parameters].[X-Axis] = 'Forest area percentage of total land area 2012' then [Forest area percentage of total land area 2012] Elseif [Parameters].[X-Axis] = 'Fossil fuels percentage of total 2012' then [Fossil fuels percentage of total 2012] Elseif [Parameters].[X-Axis] = 'Fresh water withdrawals 2005' then [Fresh water withdrawals 2005] Elseif [Parameters].[X-Axis] = 'Gender Inequality Index 2014' then [Gender Inequality Index 2014] Elseif [Parameters].[X-Axis] = 'General government final consumption expenditure - Annual growth 2005 2013' then [General government final consumption expenditure - Annual growth 2005 2013] Elseif [Parameters].[X-Axis] = 'General government final consumption expenditure - Perce of GDP 2005-2013' then [General government final consumption expenditure - Perce of GDP 2005-2013] Elseif [Parameters].[X-Axis] = 'Gross domestic product GDP 2013' then [Gross domestic product GDP 2013] Elseif [Parameters].[X-Axis] = 'Gross domestic product GDP percapta' then [Gross domestic product GDP percapta] Elseif [Parameters].[X-Axis] = 'Gross fixed capital formation of GDP 2005-2013' then [Gross fixed capital formation of GDP 2005-2013] Elseif [Parameters].[X-Axis] = 'Gross national income GNI per capita - 2011 Dollars' then [Gross national income GNI per capita - 2011 Dollars] Elseif [Parameters].[X-Axis] = 'Homeless people due to natural disaster 2005 2014 per million people' then [Homeless people due to natural disaster 2005 2014 per million people] Elseif [Parameters].[X-Axis] = 'Homicide rate per 100k people 2008-2012' then [Homicide rate per 100k people 2008-2012] Elseif [Parameters].[X-Axis] = 'Infant Mortality 2013 per thousands' then [Infant Mortality 2013 per thousands] Elseif [Parameters].[X-Axis] = 'International inbound tourists thausands 2013' then [International inbound tourists thausands 2013] Elseif [Parameters].[X-Axis] = 'International student mobility of total tetiary enrolvemnt 2013' then [International student mobility of total tetiary enrolvemnt 2013] Elseif [Parameters].[X-Axis] = 'Internet users percentage of population 2014' then [Internet users percentage of population 2014] Elseif [Parameters].[X-Axis] = 'Intimate or nonintimate partner violence ever experienced 2001-2011' then [Intimate or nonintimate partner violence ever experienced 2001-2011] Elseif [Parameters].[X-Axis] = 'Life expectancy at birth- years' then [Life expectancy at birth- years] Elseif [Parameters].[X-Axis] = 'MaleSuicide Rate 100k people' then [MaleSuicide Rate 100k people] Elseif [Parameters].[X-Axis] = 'Maternal mortality ratio deaths per 100 live births 2013' then [Maternal mortality ratio deaths per 100 live births 2013] Elseif [Parameters].[X-Axis] = 'Mean years of schooling - Years' then [Mean years of schooling - Years] Elseif [Parameters].[X-Axis] = 'Mobile phone subscriptions per 100 people 2014' then [Mobile phone subscriptions per 100 people 2014] Elseif [Parameters].[X-Axis] = 'Natural resource depletion' then [Natural resource depletion] Elseif [Parameters].[X-Axis] = 'Net migration rate per 1k people 2010-2015' then [Net migration rate per 1k people 2010-2015] Elseif [Parameters].[X-Axis] = 'Physicians per 10k people' then [Physicians per 10k people] Elseif [Parameters].[X-Axis] = 'Population affected by natural desasters average annual per million people 2005-2014' then [Population affected by natural desasters average annual per million people 2005-2014] Elseif [Parameters].[X-Axis] = 'Population living on degraded land Percentage 2010' then [Population living on degraded land Percentage 2010] Elseif [Parameters].[X-Axis] = 'Population with at least some secondary education percent 2005-2013' then [Population with at least some secondary education percent 2005-2013] Elseif [Parameters].[X-Axis] = 'Pre-primary 2008-2014' then [Pre-primary 2008-2014] Elseif [Parameters].[X-Axis] = 'Primary-2008-2014' then [Primary-2008-2014] Elseif [Parameters].[X-Axis] = 'Primary school dropout rate 2008-2014' then [Primary school dropout rate 2008-2014] Elseif [Parameters].[X-Axis] = 'Prison population per 100k people' then [Prison population per 100k people] Elseif [Parameters].[X-Axis] = 'Private capital flows percentage GDP 2013' then [Private capital flows percentage GDP 2013] Elseif [Parameters].[X-Axis] = 'Public expenditure on education Percentange GDP' then [Public expenditure on education Percentange GDP] Elseif [Parameters].[X-Axis] = 'Public health expenditure percentage of GDP 2013' then [Public health expenditure percentage of GDP 2013] Elseif [Parameters].[X-Axis] = 'Pupil-teacher ratio primary school pupils per teacher 2008-2014' then [Pupil-teacher ratio primary school pupils per teacher 2008-2014] Elseif [Parameters].[X-Axis] = 'Refugees by country of origin' then [Refugees by country of origin] Elseif [Parameters].[X-Axis] = 'Remittances inflows percentual GDP 2013' then [Remittances inflows percentual GDP 2013] Elseif [Parameters].[X-Axis] = 'Renewable sources percentage of total 2012' then [Renewable sources percentage of total 2012] Elseif [Parameters].[X-Axis] = 'Research and development expenditure 2005-2012' then [Research and development expenditure 2005-2012] Elseif [Parameters].[X-Axis] = 'Secondary 2008-2014' then [Secondary 2008-2014] Elseif [Parameters].[X-Axis] = 'Share of seats in parliament percentage held by womand 2014' then [Share of seats in parliament percentage held by womand 2014] Elseif [Parameters].[X-Axis] = 'Stock of immigrants percentage of population 2013' then [Stock of immigrants percentage of population 2013] Elseif [Parameters].[X-Axis] = 'Taxes on income profit and capital gain 205 2013' then [Taxes on income profit and capital gain 205 2013] Elseif [Parameters].[X-Axis] = 'Tertiary -2008-2014' then [Tertiary -2008-2014] Elseif [Parameters].[X-Axis] = 'Total tax revenue of GDP 2005-2013' then [Total tax revenue of GDP 2005-2013] Elseif [Parameters].[X-Axis] = 'Tuberculosis rate per thousands 2012' then [Tuberculosis rate per thousands 2012] Elseif [Parameters].[X-Axis] = 'Under-five Mortality 2013 thousands' then [Under-five Mortality 2013 thousands] END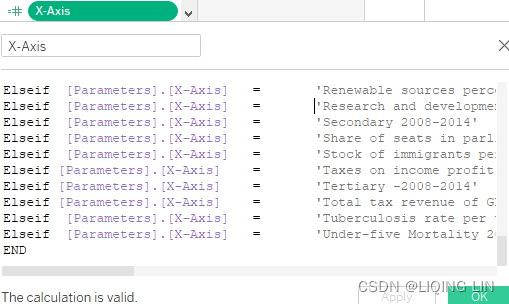
- 7. Now we will do the same thing for the Y-Axis parameter.
In order to create the calculated field for Y-Axis quicker, copy and paste the X-Axis calculated field into Excel and find and replace [Parameters].[X-Axis] with [Parameters].[Y-Axis].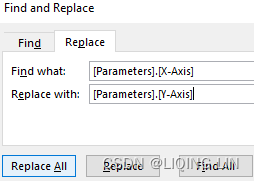
If [Parameters].[Y-Axis] = 'Human Development Index HDI-2014' then [Human Development Index HDI-2014] Elseif [Parameters].[Y-Axis] = 'Gini coefficient 2005-2013' then [Gini coefficient 2005-2013] Elseif [Parameters].[Y-Axis] = 'Adolescent birth rate 15-19 per 100k 20102015' then [Adolescent birth rate 15-19 per 100k 20102015] Elseif [Parameters].[Y-Axis] = 'Birth registration funder age 5 2005-2013' then [Birth registration funder age 5 2005-2013] Elseif [Parameters].[Y-Axis] = 'Carbon dioxide emissionsAverage annual growth' then [Carbon dioxide emissionsAverage annual growth] Elseif [Parameters].[Y-Axis] = 'Carbon dioxide emissions per capita 2011 Tones' then [Carbon dioxide emissions per capita 2011 Tones] Elseif [Parameters].[Y-Axis] = 'Change forest percentable 1900 to 2012' then [Change forest percentable 1900 to 2012] Elseif [Parameters].[Y-Axis] = 'Change mobile usage 2009 2014' then [Change mobile usage 2009 2014] Elseif [Parameters].[Y-Axis] = 'Consumer price index 2013' then [Consumer price index 2013] Elseif [Parameters].[Y-Axis] = 'Domestic credit provided by financial sector 2013' then [Domestic credit provided by financial sector 2013] Elseif [Parameters].[Y-Axis] = 'Domestic food price level 2009 2014 index' then [Domestic food price level 2009 2014 index] Elseif [Parameters].[Y-Axis] = 'Domestic food price level 2009-2014 volitility index' then [Domestic food price level 2009-2014 volitility index] Elseif [Parameters].[Y-Axis] = 'Electrification rate or population' then [Electrification rate or population] Elseif [Parameters].[Y-Axis] = 'Expected years of schooling - Years' then [Expected years of schooling - Years] Elseif [Parameters].[Y-Axis] = 'Exports and imports percentage GPD 2013' then [Exports and imports percentage GPD 2013] Elseif [Parameters].[Y-Axis] = 'Female Suicide Rate 100k people' then [Female Suicide Rate 100k people] Elseif [Parameters].[Y-Axis] = 'Foreign direct investment net inflows percentage GDP 2013' then [Foreign direct investment net inflows percentage GDP 2013] Elseif [Parameters].[Y-Axis] = 'Forest area percentage of total land area 2012' then [Forest area percentage of total land area 2012] Elseif [Parameters].[Y-Axis] = 'Fossil fuels percentage of total 2012' then [Fossil fuels percentage of total 2012] Elseif [Parameters].[Y-Axis] = 'Fresh water withdrawals 2005' then [Fresh water withdrawals 2005] Elseif [Parameters].[Y-Axis] = 'Gender Inequality Index 2014' then [Gender Inequality Index 2014] Elseif [Parameters].[Y-Axis] = 'General government final consumption expenditure - Annual growth 2005 2013' then [General government final consumption expenditure - Annual growth 2005 2013] Elseif [Parameters].[Y-Axis] = 'General government final consumption expenditure - Perce of GDP 2005-2013' then [General government final consumption expenditure - Perce of GDP 2005-2013] Elseif [Parameters].[Y-Axis] = 'Gross domestic product GDP 2013' then [Gross domestic product GDP 2013] Elseif [Parameters].[Y-Axis] = 'Gross domestic product GDP percapta' then [Gross domestic product GDP percapta] Elseif [Parameters].[Y-Axis] = 'Gross fixed capital formation of GDP 2005-2013' then [Gross fixed capital formation of GDP 2005-2013] Elseif [Parameters].[Y-Axis] = 'Gross national income GNI per capita - 2011 Dollars' then [Gross national income GNI per capita - 2011 Dollars] Elseif [Parameters].[Y-Axis] = 'Homeless people due to natural disaster 2005 2014 per million people' then [Homeless people due to natural disaster 2005 2014 per million people] Elseif [Parameters].[Y-Axis] = 'Homicide rate per 100k people 2008-2012' then [Homicide rate per 100k people 2008-2012] Elseif [Parameters].[Y-Axis] = 'Infant Mortality 2013 per thousands' then [Infant Mortality 2013 per thousands] Elseif [Parameters].[Y-Axis] = 'International inbound tourists thausands 2013' then [International inbound tourists thausands 2013] Elseif [Parameters].[Y-Axis] = 'International student mobility of total tetiary enrolvemnt 2013' then [International student mobility of total tetiary enrolvemnt 2013] Elseif [Parameters].[Y-Axis] = 'Internet users percentage of population 2014' then [Internet users percentage of population 2014] Elseif [Parameters].[Y-Axis] = 'Intimate or nonintimate partner violence ever experienced 2001-2011' then [Intimate or nonintimate partner violence ever experienced 2001-2011] Elseif [Parameters].[Y-Axis] = 'Life expectancy at birth- years' then [Life expectancy at birth- years] Elseif [Parameters].[Y-Axis] = 'MaleSuicide Rate 100k people' then [MaleSuicide Rate 100k people] Elseif [Parameters].[Y-Axis] = 'Maternal mortality ratio deaths per 100 live births 2013' then [Maternal mortality ratio deaths per 100 live births 2013] Elseif [Parameters].[Y-Axis] = 'Mean years of schooling - Years' then [Mean years of schooling - Years] Elseif [Parameters].[Y-Axis] = 'Mobile phone subscriptions per 100 people 2014' then [Mobile phone subscriptions per 100 people 2014] Elseif [Parameters].[Y-Axis] = 'Natural resource depletion' then [Natural resource depletion] Elseif [Parameters].[Y-Axis] = 'Net migration rate per 1k people 2010-2015' then [Net migration rate per 1k people 2010-2015] Elseif [Parameters].[Y-Axis] = 'Physicians per 10k people' then [Physicians per 10k people] Elseif [Parameters].[Y-Axis] = 'Population affected by natural desasters average annual per million people 2005-2014' then [Population affected by natural desasters average annual per million people 2005-2014] Elseif [Parameters].[Y-Axis] = 'Population living on degraded land Percentage 2010' then [Population living on degraded land Percentage 2010] Elseif [Parameters].[Y-Axis] = 'Population with at least some secondary education percent 2005-2013' then [Population with at least some secondary education percent 2005-2013] Elseif [Parameters].[Y-Axis] = 'Pre-primary 2008-2014' then [Pre-primary 2008-2014] Elseif [Parameters].[Y-Axis] = 'Primary-2008-2014' then [Primary-2008-2014] Elseif [Parameters].[Y-Axis] = 'Primary school dropout rate 2008-2014' then [Primary school dropout rate 2008-2014] Elseif [Parameters].[Y-Axis] = 'Prison population per 100k people' then [Prison population per 100k people] Elseif [Parameters].[Y-Axis] = 'Private capital flows percentage GDP 2013' then [Private capital flows percentage GDP 2013] Elseif [Parameters].[Y-Axis] = 'Public expenditure on education Percentange GDP' then [Public expenditure on education Percentange GDP] Elseif [Parameters].[Y-Axis] = 'Public health expenditure percentage of GDP 2013' then [Public health expenditure percentage of GDP 2013] Elseif [Parameters].[Y-Axis] = 'Pupil-teacher ratio primary school pupils per teacher 2008-2014' then [Pupil-teacher ratio primary school pupils per teacher 2008-2014] Elseif [Parameters].[Y-Axis] = 'Refugees by country of origin' then [Refugees by country of origin] Elseif [Parameters].[Y-Axis] = 'Remittances inflows percentual GDP 2013' then [Remittances inflows percentual GDP 2013] Elseif [Parameters].[Y-Axis] = 'Renewable sources percentage of total 2012' then [Renewable sources percentage of total 2012] Elseif [Parameters].[Y-Axis] = 'Research and development expenditure 2005-2012' then [Research and development expenditure 2005-2012] Elseif [Parameters].[Y-Axis] = 'Secondary 2008-2014' then [Secondary 2008-2014] Elseif [Parameters].[Y-Axis] = 'Share of seats in parliament percentage held by womand 2014' then [Share of seats in parliament percentage held by womand 2014] Elseif [Parameters].[Y-Axis] = 'Stock of immigrants percentage of population 2013' then [Stock of immigrants percentage of population 2013] Elseif [Parameters].[Y-Axis] = 'Taxes on income profit and capital gain 205 2013' then [Taxes on income profit and capital gain 205 2013] Elseif [Parameters].[Y-Axis] = 'Tertiary -2008-2014' then [Tertiary -2008-2014] Elseif [Parameters].[Y-Axis] = 'Total tax revenue of GDP 2005-2013' then [Total tax revenue of GDP 2005-2013] Elseif [Parameters].[Y-Axis] = 'Tuberculosis rate per thousands 2012' then [Tuberculosis rate per thousands 2012] Elseif [Parameters].[Y-Axis] = 'Under-five Mortality 2013 thousands' then [Under-five Mortality 2013 thousands] END
最低0.47元/天 解锁文章
扫一扫
2万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
