后缀数组各个变量含义

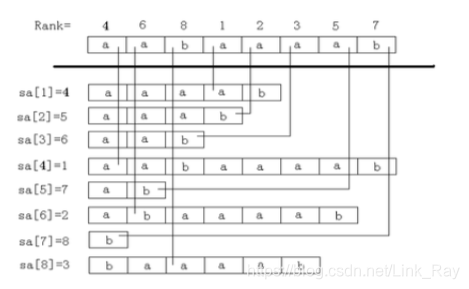
1. sa[i] = j: 代表第i名的后缀是[j,n]。
2. rank[i] = j: 代表后缀[i,n]是第j名。
3. height[i] = j: 第i名与第i-1名的LCP是j。

https://ac.nowcoder.com/acm/contest/551/C
询问长度大于k的不同子串个数。

每个子串都是一个后缀的前缀，所以一个后缀加入会贡献出n-sa[i]+1个子串。
例如后缀aaabbc，贡献的子串有aaabbc,aaabb,aaab,aaa,aa,a。扣除掉与前面重复出现的子串就是新贡献的子串个数:n-sa[i]+1-height[i]。假设height[i]=1，k=3，height淘汰了a，但是aa也是不满足的，所以对于长度大于k的，只需n-sa[i]+1-max(height[i],k-1)即可。

sa[i]下标从0开始

#include<iostream>
#include<cstdio>
using namespace std;
const int N=1e5+100;
const int M=1e5+100;
int wa[N],wb[N],wv[N],wss[M];
string tr;
int r[N],sa[N];
int cmp(int *r,int a,int b,int l)
{return r[a]==r[b]&&r[a+l]==r[b+l];}
void da(int *r,int *sa,int n,int m)
{
    int i,j,p,*x=wa,*y=wb,*t;
    for(i=0;i<m;i++) wss[i]=0;
    for(i=0;i<n;i++) wss[x[i]=r[i]]++;
    for(i=1;i<m;i++) wss[i]+=wss[i-1];
    for(i=n-1;i>=0;i--) sa[--wss[x[i]]]=i;
    for(j=1,p=1;p<n;j*=2,m=p)
    {
        for(p=0,i=n-j;i<n;i++) y[p++]=i;
        for(i=0;i<n;i++) if(sa[i]>=j) y[p++]=sa[i]-j;
        for(i=0;i<n;i++) wv[i]=x[y[i]];
        for(i=0;i<m;i++) wss[i]=0;
        for(i=0;i<n;i++) wss[wv[i]]++;
        for(i=1;i<m;i++) wss[i]+=wss[i-1];
        for(i=n-1;i>=0;i--) sa[--wss[wv[i]]]=y[i];
        for(t=x,x=y,y=t,p=1,x[sa[0]]=0,i=1;i<n;i++)
        x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
    }
    return;
}
int rankk[N],height[N];
void calheight(int *r,int *sa,int n)
{
    int i,j,k=0;
    for(i=1;i<=n;i++) rankk[sa[i]]=i;
    for(i=0;i<n;height[rankk[i++]]=k)
    for(k?k--:0,j=sa[rankk[i]-1];r[i+k]==r[j+k];k++);
    return;
}
int main()
{
    int n,mm,k;
    int m=1000;
    long long ans;
    cin>>n>>mm;
    cin>>tr;
    for(int i=0;i<n;++i)
        r[i]=(int)(tr[i])+1;
    r[n]=0;
    da(r,sa,n+1,m);
    calheight(r,sa,n);
    ans=0;
   // for(int i = 1; i <= n; ++i) cout << sa[i] << endl;
    for(int i=1;i<=n;++i)
        ans+=max(0,n-sa[i]-max(mm-1,height[i]));
    printf("%lld\n",ans);
    return 0;
}