Leetcode 50 pow（x，n）

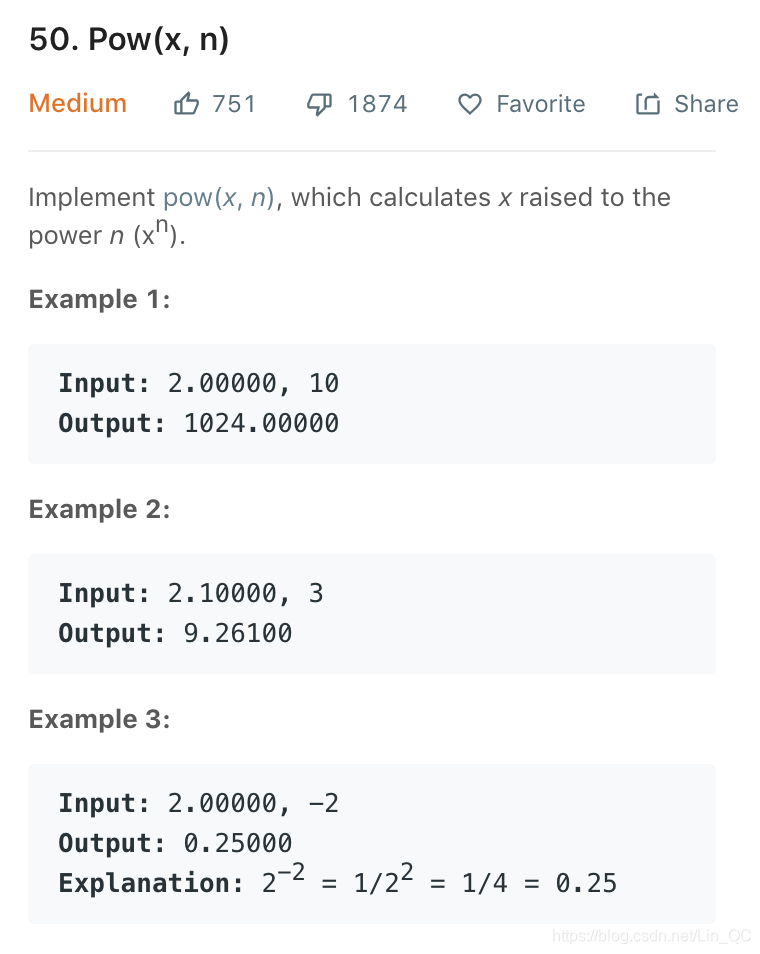
这就是一题实现求解高次方的题目

一开始想到的是简单的逐个相乘，例如2^4=2*2*2*2.

class Solution {
    public double myPow(double x, int n) {
        double sum=1;
        if(n==0) return 1;
        for(int i=1;i<=Math.abs(n);i++){
            sum*=x;
        }
        if(n>0) return sum;
        else return 1/sum;
    }
}

不幸的是，它超时了，其实也在意料之中，毕竟这题标记的难度是medium ，不可能这么easy。

思索着使用 分治法，去掉一些多余的运算。 

例如2^10，我们可以先计算2^5，之后将两个2^5相乘得到结果，这样我们就省去了一半的工作，也就是计算第二个2的五次方；而对于2^5，我们又可以进行拆分，由于5是奇数，我们可以看成两个2^2相乘再乘上2；之后再依次拆分。

具体代码如下（具体代码中考虑了n为负的情况）

class Solution {
    public double myPow(double x, int n) {
        if(n==0) return 1;
        double temp=myPow(x,n/2);
        if(n>0)
        return n%2==0?temp*temp:x*temp*temp;
        else
        return n%2==0?temp*temp:temp*temp/x;
    }
}