sklearn中的线性回归#02

最新推荐文章于 2025-11-30 15:25:22 发布

原创

最新推荐文章于 2025-11-30 15:25:22 发布 · 528 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#sklearn #线性回归 #机器学习

本文探讨了线性回归中的非线性问题，通过多项式回归来处理非线性关系。线性关系指的是变量间可通过直线拟合，而如三角函数、高次函数等则呈现非线性关系。使用线性回归模型的效果可判断数据的线性与否，线性可分的数据在分类问题中很重要。

文章目录

非线性问题：多项式回归
- 变量之间的线性关系
- 数据的线性与非线性

非线性问题：多项式回归

变量之间的线性关系

我们最常使用的线性是指“变量之间的线性关系（linear
relationship）”，它表示两个变量之间的关系可以展示为一条直线，即可以使用方来进行拟合。要探索两个变量之间的关系是否是线性的，最简单的方式就是绘制散点图，如果散点图能够相对均匀地分布在一条直线的两端，则说明这两个变量之间的关系是线性的。因此，三角函数( )，高次函数 )，指数函数( )等等图像不为直线的函数所对应的自变量和因变量之间是非线性关系（non-linear relationship）。
也因此被称为线性方程或线性函数（linear function），三角函数，高次函数等也因此被称为非线性函数
（non-linear function）。
在这里插入图片描述

数据的线性与非线性

对于线性和非线性数据，最简单的判别方法就是利用模型来帮助我们——如果是做分类则使用逻辑回归，如果做回归则使用线性回归，如果效果好那数据是线性的，效果不好则数据不是线性的。当然，也可以降维后进行绘图，绘制出的图像分布接近一条直线，则数据就是线性的。
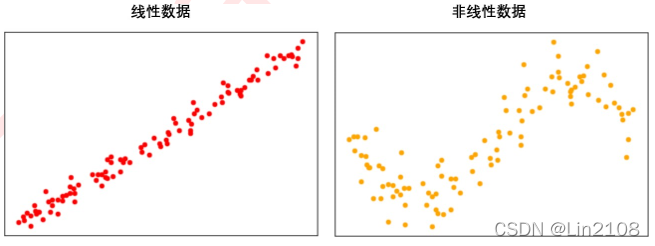
在这里插入图片描述
在分类数据中，我们使用“是否线性可分”（linearly separable）这个概念来划分分类数据集。当分类数据的分布上可以使用一条直线来将两类数据分开时，我们就说数据是线性可分的。反之，数据不是线性可分的。
总结一下，对于回归问题，数据若能分布为一条直线，则是线性的，否则是非线性。对于分类问题，数据分布若能使用一条直线来划分类别，则是线性可分的，否则数据则是线性不可分的。