[翻译]扫描线算法(Line Sweep Algorithm)（2）

最新推荐文章于 2024-05-30 22:39:06 发布

翻译最新推荐文章于 2024-05-30 22:39:06 发布 · 1w 阅读

文章标签：

#算法 #扫描线

计算几何专栏收录该内容

3 篇文章

订阅专栏

本文介绍了一种利用扫描线技术解决多个矩形重叠部分面积计算问题的方法。通过两次扫描线过程，分别沿水平和垂直方向计算矩形重叠区域的宽度和高度，最终得出重叠面积。

NOIPD110分滚粗。
心累。
学点有趣的治愈一下。
突然想起似乎之前还有个坑没有填，就练一波英语阅读。

矩形面积交

给出一个集合包含N个与坐标轴对称的矩形（矩形的边与x轴、y轴平行），找到所有的矩形的重叠部分。其中一个矩形由两个点代表，一个是左下角的点，一个是右上角的点。
这个问题的事件，是垂直的边。当我们遇到一条左边，我们进行一些操作；遇到一条右边，进行另一些操作。左边由左下角来代表，右边由右上角代表。
我们以对x坐标的排序来开始整个算法。当一个长方形左下角的点被遇到（也就是说我们遇到了长方形的左边），我们将之插入到集合中。当我们遇到了右上角的点（也就是遇到了长方形的右边），我们将长方形从集合中清除出去。在任何情况，集合中只存在被扫描线扫到的矩形（即已遇到左边但未遇到右边）。
扫到的面积是Δy*Δx，其中Δy是扫描线被矩形切割的长度（下图中的红色部分），Δx为两个扫描线事件之间的距离。
但是现在我们只知道哪些是被扫描线被切割的矩形。因此，这里我们有一个新的问题：如何找到被切割的最大长度？
其做法与我们刚才（参见上一篇）做的类似。我们仍然用扫描线技术，不过这条线现在要旋转90°，换言之，我们从下到上去扫描被扫到的矩形。我们用一个变量cnt维护当前重叠的矩形数量。当我们遇到一条底边就让cnt+1，遇到一条上边就让cnt-1，当cnt从非0变为0时我们就找到了扫描线被切割的长度。
下面来看看它是如何运行的。

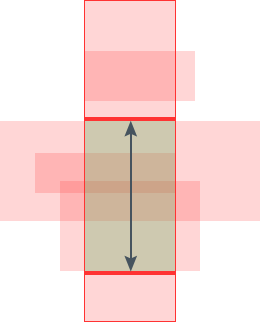
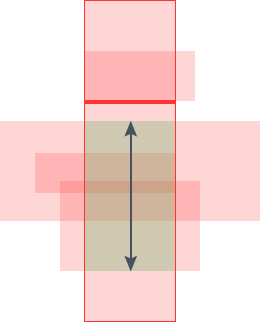
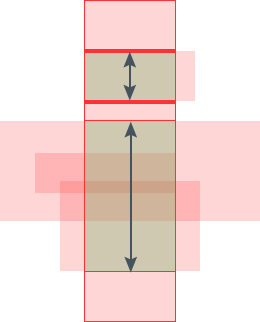
上面的图像向我们展示了水平扫描线的运行过程， Δy 就是最后一张图片展示的两个箭头长度之和。
这就是我们的算法，接下来考虑枚举的部分。对于每一个扫描线的事件，我们需要找到扫描线切出的长度，也就是推进水平扫描线长度。这里以bool数组作为数据结构，因为我们可以分别以横、纵来做一次排序。
下面是cpp代码：

#define MAX 1000
struct event 
{
    int ind; // 众多矩形中该矩形的索引
    bool type; // 事件类型，0表示左下，1表示右上
    event() {};
    event(int ind, int type) : ind(ind), type(type) {};
};
struct point 
{
    int x, y;
};
point rects [MAX][12]; // 每个矩形包含两个顶点: [0]=左下;[1]=右上
bool compare_x(event a, event b) { 
    return rects[a.ind][a.type].x<rects[b.ind][b.type].x; 
}
bool compare_y(event a, event b) { 
    return rects[a.ind][a.type].y<rects[b.ind][b.type].y; 
}
int union_area(event events_v[],event events_h[],int n,int e)
{
       //n是矩形数量, e=2*n , e是顶点数量(在矩形集合中每个矩形以两个点被申明)
        bool in_set[MAX]={0};
        int area=0;
        sort(events_v, events_v+e, compare_x);  //竖直边的预处理
        sort(events_h, events_h+e, compare_y); // 水平边的预处理
        in_set[events_v[0].ind] = 1;
        for (int i=1;i<e;++i) 
        { // 水平扫描线
                event c = events_v[i];
                int cnt = 0; // 表明有多少矩形重叠的计数器
                // Delta_x: 当前线与之前线的距离
                int delta_x = rects[c.ind][c.type].x - rects[events_v[i-1].ind][events_v[i-1].type].x;
                int begin_y;
                if (delta_x==0){
                        in_set[c.ind] = (c.type==0);
                        continue;
                }
                for (int j=0;j<e;++j)
                        if (in_set[events_h[j].ind]==1)                 //当前矩形的水平扫描线
                        {
                                if (events_h[j].type==0)                //是底边
                                {
                                        if (cnt==0) begin_y = rects[events_h[j].ind][0].y; // 某一块开始
                                        ++cnt;                          //重叠矩形增加量
                                }
                                else    //是上面的线
                                {
                                        --cnt;                          //矩形已经不被重叠，所以移除之
                                        if (cnt==0)                     //一块的结束
                                        {
                                                int delta_y = (rects[events_h[j].ind][13].y-begin_y);//竖直扫描线被切割的长度
                                                area+=delta_x * delta_y;
                                        }
                                }
                        }
                in_set[c.ind] = (c.type==0);//如果是左边, 矩形在当前集合中，否则不在
        }
    return area;
}