《计算机视觉：算法与应用 第二版》学习1

第2章 图像形成（Image Formation）

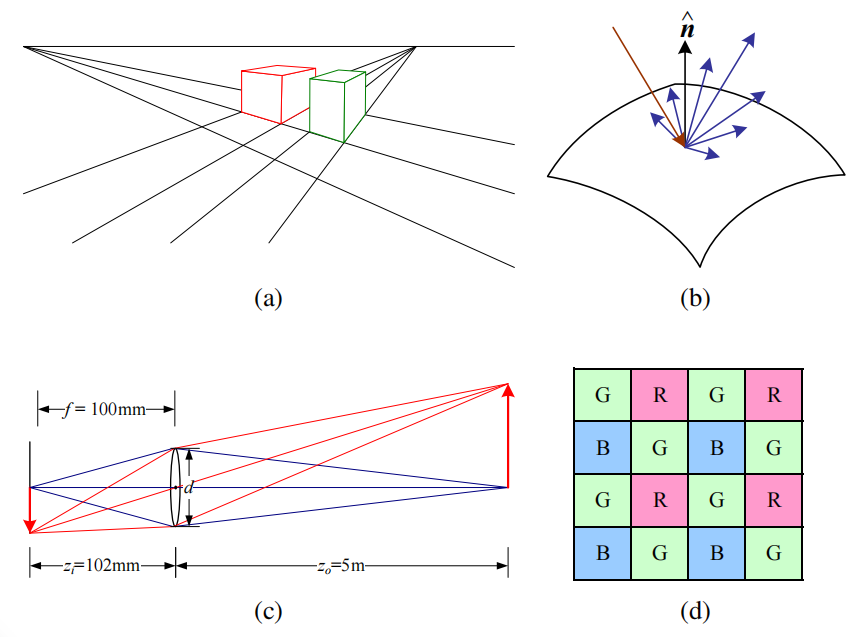
图 2.1 (a)透视投影；(b)光线在撞击表面时的散射；(c ) 镜头光学；(d)Bayer彩色滤光阵列

本章核心目标：
在分析和处理图像之前，必须建立对场景几何和图像形成过程的理解。这一章提出了一个简化的图像形成模型，帮助理解以下关键问题：
        图像是如何由场景几何、光照、表面属性和相机光学共同作用形成的？

章节结构与要点：
🔷 2.1 几何建模与投影

• 引入了几何图元（点、线、平面）
• 介绍了如何通过几何变换将三维物体投影成二维图像特征（如图 2.1a）

🔷 2.2 光度建模（Photometric Image Formation）

• 探讨光照、物体表面属性（如反射率）与相机光学系统的相互作用
• 解释这些因素如何决定最终落在图像传感器上的颜色值（如图 2.1b 和 2.1c）

🔷 2.3 数字图像采样

• 说明连续的光强如何被离散地采样成数字图像（如图 2.1d）
• 探讨采样问题（如混叠 aliasing）以及如何避免或建模这些问题

总结一句话：
本章搭建了理解图像从真实世界到数字图像转换过程的桥梁，涵盖从几何建模、光照反射到相机采样的完整链路，是理解后续视觉算法的基石。

2.1 几何图元与变换（Geometric primitives and transformations）

本节核心目标：
建立图像几何基础：理解2D与3D中点、线、面的表示方法及其在投影变换中的作用，是后续图像建模、标定与重建的前提。

一、二维几何图元（2D Primitives）

1. 2D 点（Points）
   
2. 2D 直线（Lines）
   
3. 2D 点线运算
   
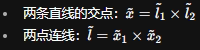
4. 2D 二次曲线（Conics）
   

二、三维几何图元（3D Primitives）

1. 3D 点（Points）
   
2. 3D 平面（Planes）
   
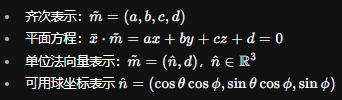
3. 3D 直线（Lines）
   
4. 3D 二次曲面（Quadrics）
   

三、图元与变换的关系
几何图元（点、线、面）是图像几何建模的基础构件，通过各种**变换（仿射、投影）**可以描述从3D世界到2D图像的投影关系。相关变换将在下一节继续展开。

总结一句话：
掌握二维与三维中点、线、面及其齐次表示，是理解相机成像、图像变换和三维重建的基础，后续章节中将基于这些几何构件构建图像处理与视觉模型。

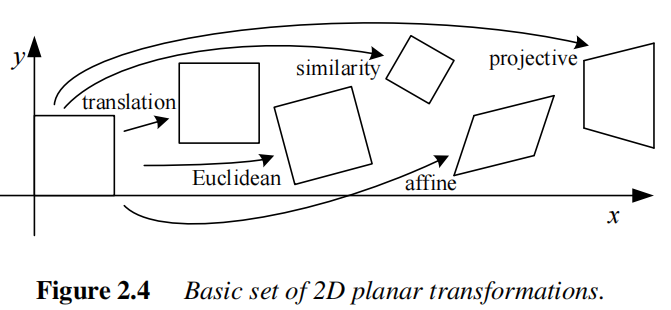
图2.4 二维平面变换基础集

2.1.1 二维变换（2D transformations）

核心目标：
掌握将二维图像中的几何对象（点、线）进行各种几何变换的方法，并理解这些变换之间的层级关系。

常见的二维几何变换类型：

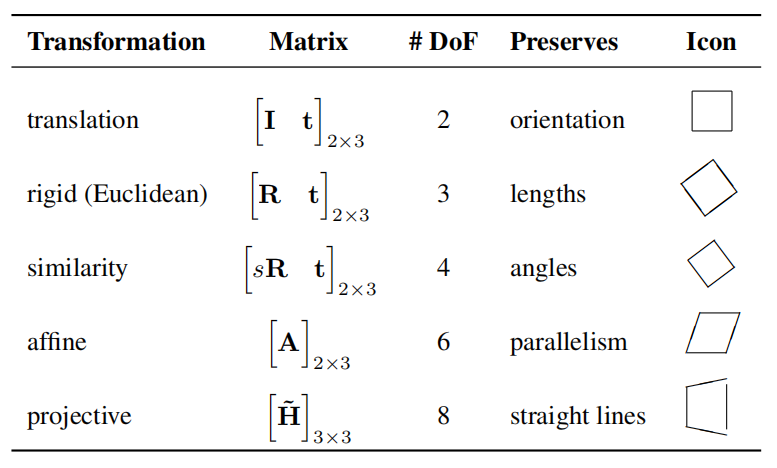
表2.1 变换类型：平移、刚体变换、相似变换、放射变换、投影变换

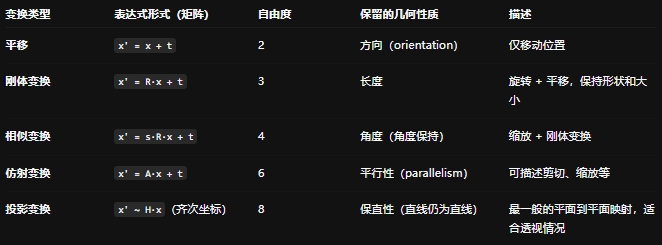
注：2×3 矩阵可通过添加 [0^T, 1] 扩展为 3×3 矩阵，用于齐次坐标变换。

变换矩阵的嵌套关系（子群）：
每种变换类型是下一种更一般变换的特例：
Translation ⊂ Rigid (Euclidean) ⊂ Similarity ⊂ Affine ⊂ Projective
这些变换满足群的性质：封闭、存在逆元素，可组合。

其他常见扩展变换：

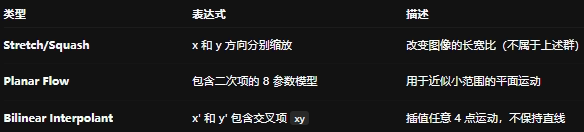
🔎 应用提示：

• 投影变换（Projective/Homography）是图像配准、相机建模、结构光等任务的核心工具。
• 各类变换适用于不同精度、自由度要求的视觉任务。
• 齐次坐标形式使得变换组合和逆运算更为方便。

2.1.2 三维变换（3D transformations）

整体结构与层级关系

• 3D坐标变换和2D类似，也构成嵌套的变换群，例如 SE(3)、Sim(3) 等。
• 每种变换都可以通过矩阵作用于齐次坐标来表示（3×4或4×4矩阵）。
• 每种变换都保留其下层变换的几何性质。

各类3D变换类型一览

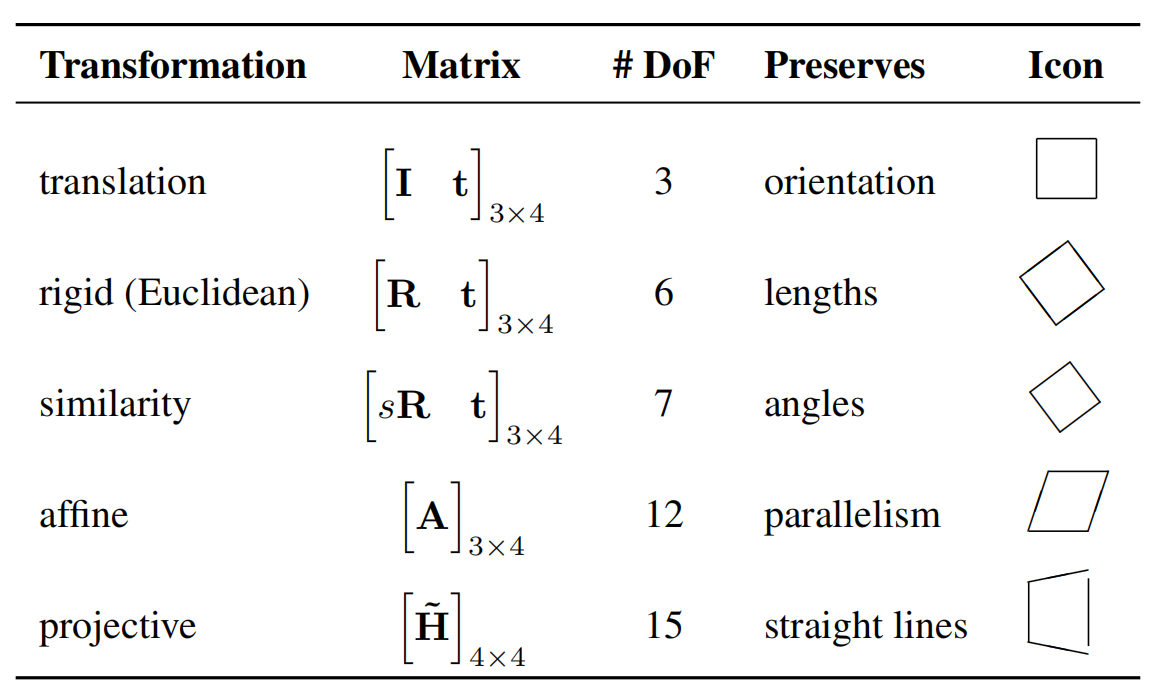
包含平移、刚体（欧式）、相似变换、仿射变换、投影变换。
几何属性对应方向、长度、角度、平行性、直线性。

各类变换详解
🔹 1. 平移 (Translation)

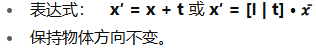
🔹 2. 刚体变换 (Rigid / Euclidean / SE(3))

🔹 3. 相似变换 (Similarity)

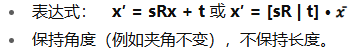
🔹 4. 仿射变换 (Affine)

🔹 5. 投影变换 (Projective / Perspective / Homography)

注意点：

• 所有变换都作用于齐次坐标向量（homogeneous coordinates）。
• 多数应用（如相机投影、图像变形）最终都会涉及projective变换。
• 与2D类似，3D刚体与投影变换也具有 Lie 群结构（SE(3)、SO(3) 等）。

2.1.3 三维旋转（3D rotations）

3D旋转的表示和参数化

• 区别于2D旋转，3D旋转的参数化更复杂，存在多种表示方式，各有优缺点。

Euler角（欧拉角）

• 通过绕三个固定轴（如x、y、z）依次旋转得到旋转矩阵。
• 缺点：
• • 旋转结果依赖旋转顺序。
• • 参数空间不连续，可能发生“万向锁”（Gimbal Lock），导致角度剧烈变化。
• 因此不推荐使用，除非在特定场景（如云台运动）较直观。
  

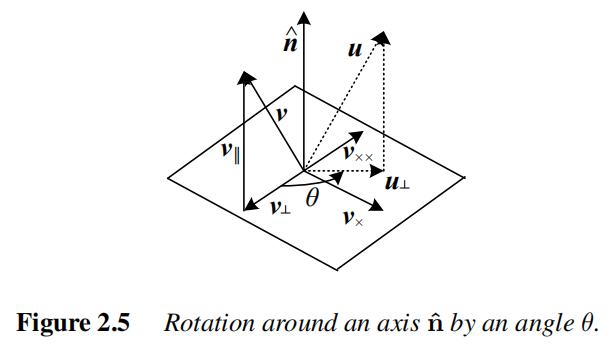
轴/角表示（Axis/Angle）

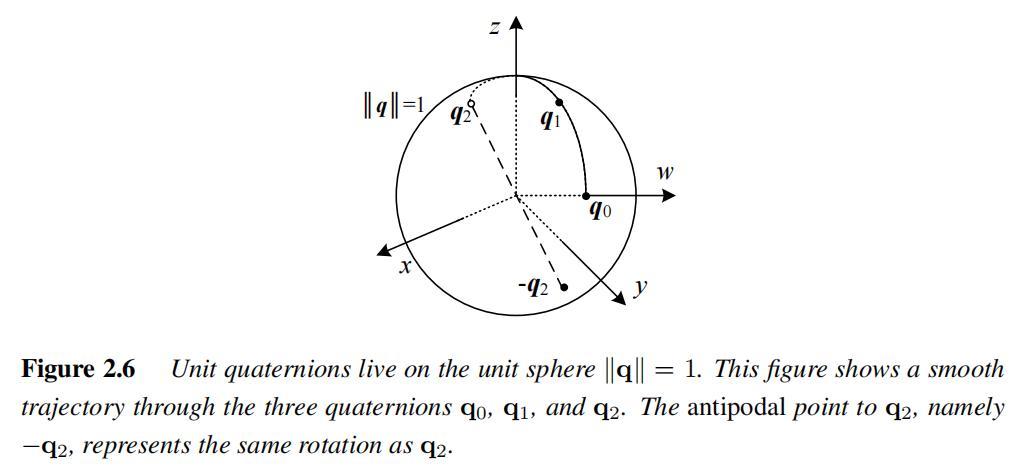
单位四元数（Unit Quaternions）

旋转表示选择建议

2.1.4 三维到二维的投影（3D to 2D projections）

3D到2D投影基础

• 目标：将3D空间点投影到2D图像平面。
• 使用线性投影矩阵表示转换关系。
• 投影模型分为：
  正射投影（Orthographic）
  透视投影（Perspective）

正射投影与准透视投影

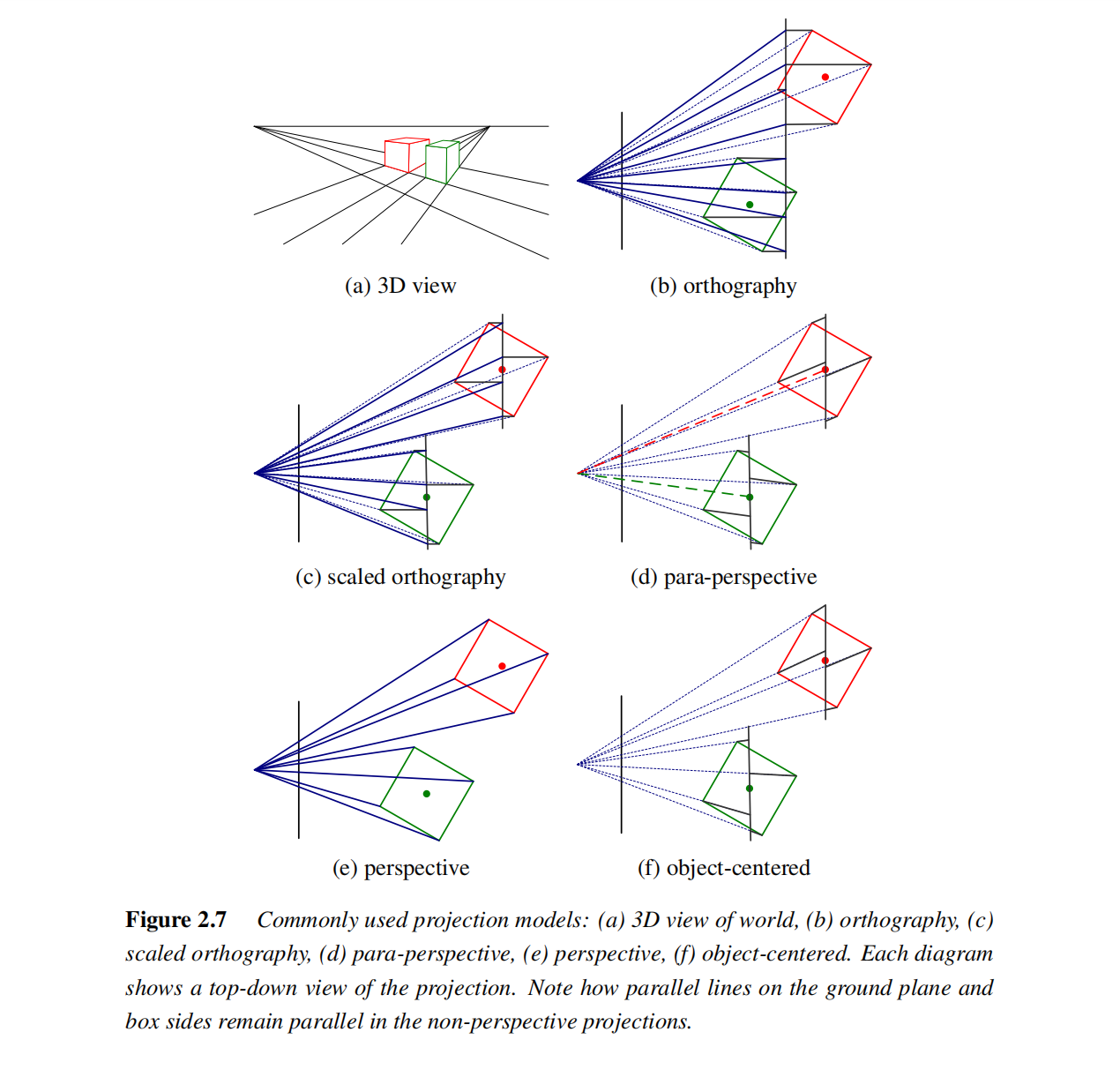
总结

• 正射和准透视投影均属于线性或仿射投影，计算简单，适合深度变化小或远距离场景。
• 这些模型在视觉任务（如结构重建、相机位姿估计）中广泛使用，因其简化计算且保持重要几何特性。
• 真实摄像头成像更符合透视投影模型，但复杂度较高，需引入非线性除法。

透视投影基本原理

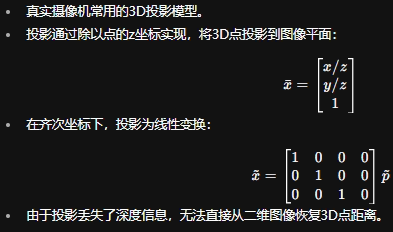
计算机图形中的透视投影实现

透视投影的特殊情况和便利性

深度与3D点恢复

• 普通2D相机无法直接测距。
• 通过深度传感器或立体匹配算法可获取深度信息。
• 若投影矩阵是满秩4×4矩阵，则可通过逆矩阵将深度或视差映射回3D点。

附图说明

• 图示说明相机中心、传感器坐标系及像素间距等概念，帮助理解投影过程。
  
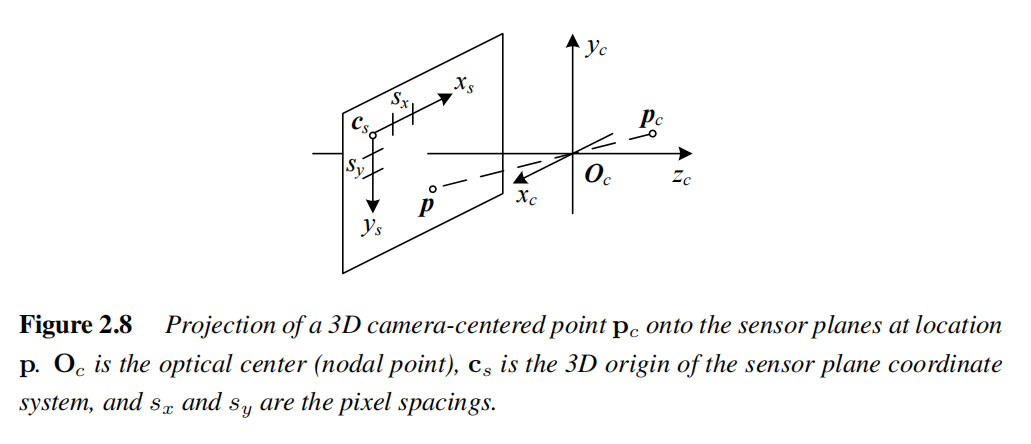
  相机内参的意义
  
  标定矩阵 𝐾
  
  常用简化形式
  
  标定与外参的关系
  
  直观示意
  
  
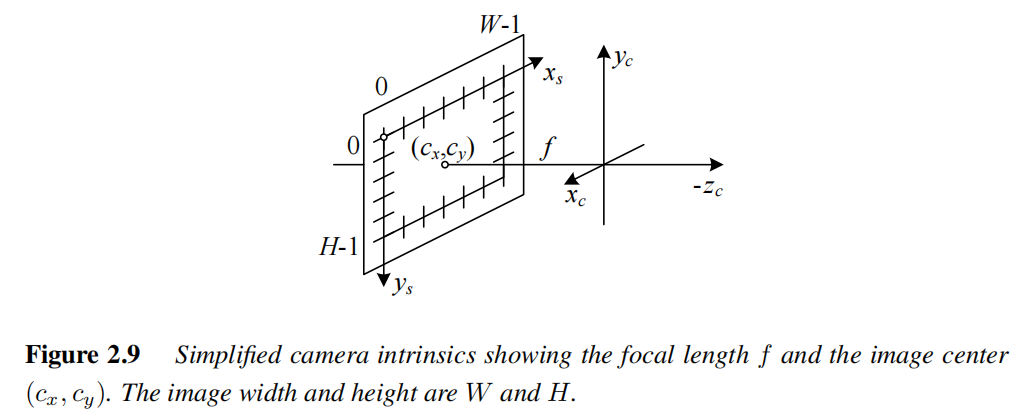
  焦距表达的困惑
  
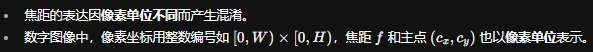
  焦距与视场角的关系
  
  像素单位与物理单位的转换
  
  归一化设备坐标（Normalized Device Coordinates）
  
  标准化焦距的优势
  
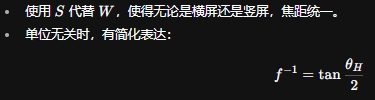
  焦距单位转换
  
  Camera matrix（相机矩阵）

1. 相机矩阵的组成
   

2. 4×4 可逆相机矩阵
   

3. 从 3D 世界坐标到屏幕坐标（含视差）
   

4. 深度的两种表示
   

5. 应用意义
   
   
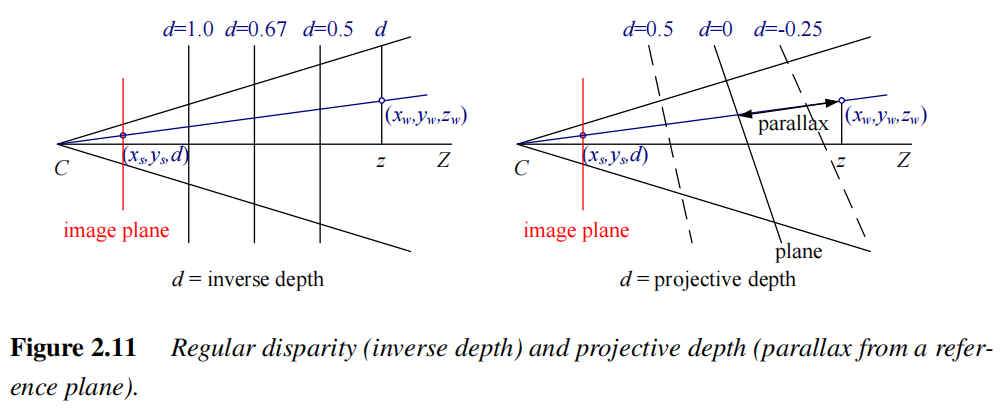
   Plane plus parallax（投影深度）

6. 背景与自由度
   

7. 一般形式
   

8. 投影深度（Projective depth）
   

9. 从像素+深度回到 3D
   

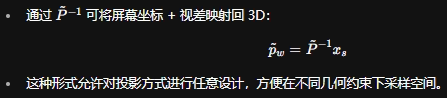
10. 应用价值

• 多视图立体（MVS）：可以灵活定义参考平面，按视差采样空间
• 平面扫描（plane sweeping）：可根据图像运动模式调整采样分布
• 几何建模与渲染：投影深度不仅能表达几何，还能优化匹配与重建精度

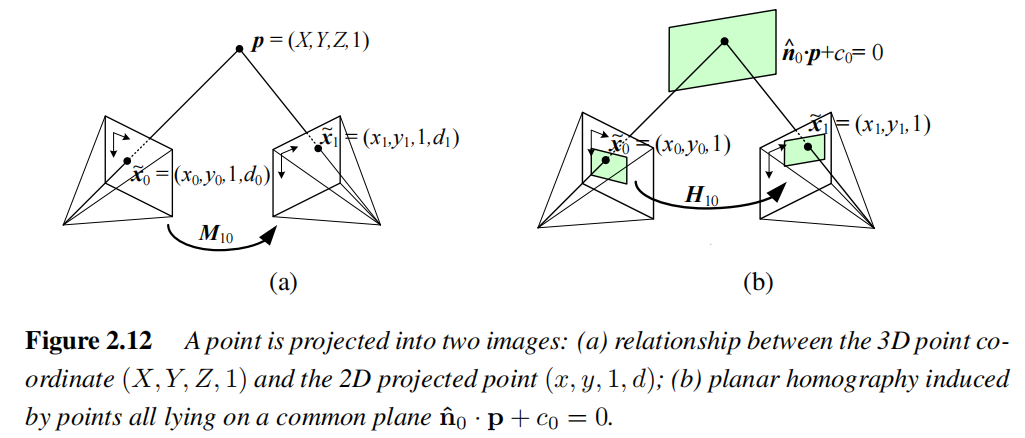
从一个相机映射到另一个相机 的方法

1. 一般三维到二维映射
   
2. 特殊情况一：平面场景（Plane-Induced Homography）
   
3. 特殊情况二：纯旋转（Pure Rotation）
   
   精简总结：
   
   这一节主要讨论长焦镜头下物距与焦距难以区分的问题，并给出了一个数学重写方法来分离这两个因素。

核心问题

数学推导

好处

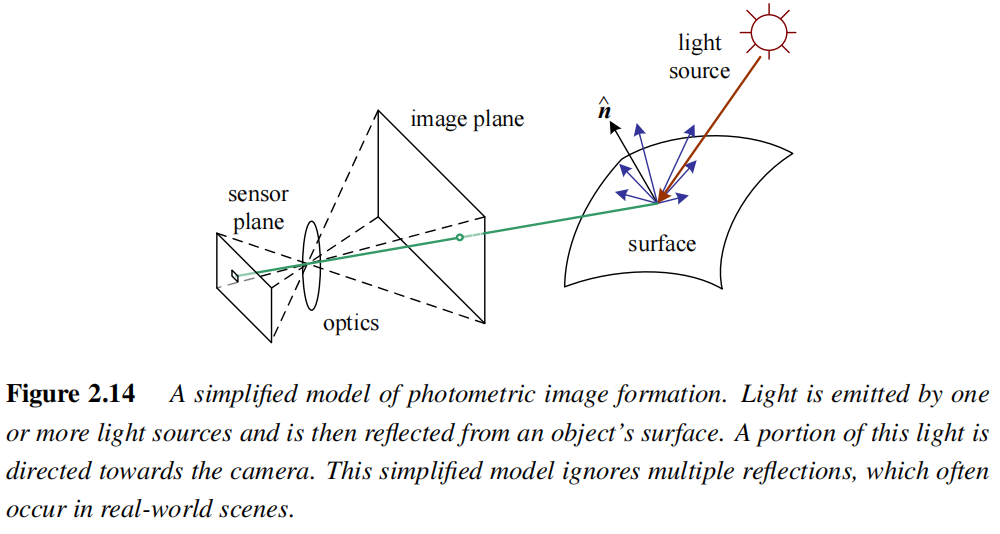
2.1.5 镜头畸变（Lens distortions）

线性投影假设的破坏

• 理想模型：直线物体投影到图像仍是直线（线性矩阵运算）。
• 现实中：广角镜头存在径向畸变（radial distortion），直线会弯曲。
• 如果不校正畸变，高精度重建会出错，例如拼接图像会出现模糊。

径向畸变建模

更复杂的畸变情况

数学处理上的注意点

• 畸变引入非线性，投影矩阵与旋转矩阵不能简单组合成上三角形式。
• 若校正到直线恢复，可视为恢复了线性成像模型，原有的分解方法依然适用。