二叉树的最大深度

Learner_QUN

已于 2023-03-21 09:50:15 修改

阅读量895

点赞数 1

分类专栏： LeetCode练习文章标签：算法数据结构 c++

于 2023-03-20 12:04:05 首次发布

本文链接：https://blog.youkuaiyun.com/Learner_QUN/article/details/129664522

版权

LeetCode练习专栏收录该内容

77 篇文章

订阅专栏

文章介绍了如何使用递归法（后序遍历和前序遍历）以及迭代法（层序遍历）来找出二叉树的最大深度。在递归法中，后序遍历计算根节点的高度，前序遍历计算到根节点的路径长度。迭代法通过队列实现层序遍历，记录遍历的层数作为最大深度。所有方法的时间复杂度均为O(N)，其中N是二叉树节点数。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1题目

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：

给定二叉树 [3,9,20,null,null,15,7]，

/ \

9 20

/ \

15 7

返回它的最大深度 3 。

2链接

题目：104. 二叉树的最大深度 - 力扣（Leetcode）

视频：二叉树的高度和深度有啥区别？究竟用什么遍历顺序？很多录友搞不懂 | LeetCode：104.二叉树的最大深度_哔哩哔哩_bilibili

3解题思路

3.1递归法

本题可以使用前序（中左右），也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序求的是高度。

二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）

二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数后者节点数（取决于高度从0开始还是从1开始）

而根节点的高度就是二叉树的最大深度，所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。

先用后序遍历（左右中）来计算树的高度。

确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回这棵树的深度，所以返回值为int类型。

代码如下：

intgetdepth(treenode* node)

确定终止条件：如果为空节点的话，就返回0，表示高度为0。

代码如下：

if(node ==NULL)return0;

确定单层递归的逻辑：先求它的左子树的深度，再求右子树的深度，最后取左右深度最大的数值再+1 （加1是因为算上当前中间节点）就是目前节点为根节点的树的深度。

代码如下：

int leftdepth = getdepth(node->left);       // 左
int rightdepth = getdepth(node->right);     // 右
int depth = 1 + max(leftdepth, rightdepth); // 中
return depth;

后序遍历解释：

该代码通过递归方式计算每个节点的深度，再求出所有节点深度的最大值，从而得到二叉树的最大深度。具体实现可以分为两个方法：

getDepth 方法用于计算单个节点的深度，采用了递归方式：

首先进行特判，如果当前节点为空（即已经递归到了叶子节点的子节点），则返回 0。

然后分别递归求解左右子树的深度，并记录在 leftDepth 和 rightDepth 变量中。

最后将左右子树深度的最大值加 1，即为当前节点的深度，记录在 Depth 变量中，并返回。

maxDepth 方法用于计算整棵二叉树的最大深度，直接调用 getDepth 方法即可。

总体来说，该算法时间复杂度为 O(N)，其中 N 是二叉树的节点数。因为需要遍历每个节点，所以时间复杂度至少为线性级别。

前序遍历也可以，代码会在最后体现，解释：

该代码同样采用了递归方式计算二叉树的最大深度，不同之处在于：

getDepth 函数中计算当前节点到根节点的深度，并与 result 变量比较，选择较大值更新 result。

对于非叶子节点，如果存在左子树，则递归调用 getDepth 函数访问左子树，并将深度加 1；如果存在右子树，则同理访问右子树。

总体来说，该算法时间复杂度为 O(N)，其中 N 是二叉树的节点数。因为需要遍历每个节点，所以时间复杂度至少为线性级别。

3.2迭代法

使用迭代法的话，使用层序遍历是最为合适的，因为最大的深度就是二叉树的层数，和层序遍历的方式极其吻合。

在二叉树中，一层一层的来遍历二叉树，记录一下遍历的层数就是二叉树的深度，如图所示：

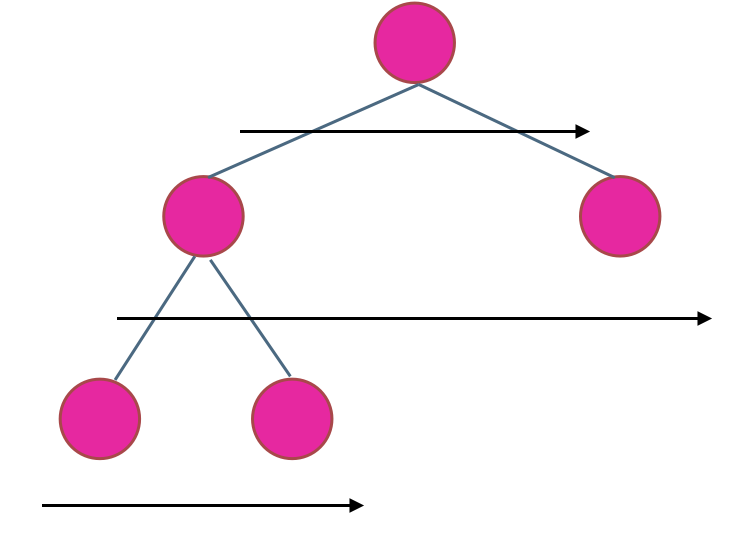
所以这道题的迭代法就是一道模板题，可以使用二叉树层序遍历的模板来解决的。

迭代法解释：

该代码采用了迭代法-层序遍历的方式来计算二叉树的最大深度。具体步骤如下：

首先判断根节点是否为空，若为空则直接返回0。

创建一个队列 que，并将根节点入队。

初始化深度变量 depth 为 0，表示从根节点开始。

开始循环，每次访问一层的节点。在每次循环中：

a. 深度变量 depth 加 1，记录下当前所在层数。

b. 获取当前层的节点数 level_size，即当前队列的元素个数。

c. 遍历当前层的所有节点，依次取出队首元素，将其左右子节点入队。

如果队列为空，说明已经遍历完了整棵树，返回最大深度 depth。

整个算法的时间复杂度是O(N)，其中 N 是二叉树的节点个数。因为需要遍历每个节点一次，所以时间复杂度至少为线性级别。而空间复杂度则取决于队列的大小，最坏情况下所有节点都在同一层，队列的大小就是 O(N)。

综上所述，该算法的时间复杂度和空间复杂度都比较优秀，且实现简单易懂。

4代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
//递归法-后序遍历
class Solution {
public:
    // 用于计算指定节点的深度
    int getDepth(TreeNode* node) {
        if (node == nullptr) return 0; // 特判：如果当前节点为空，则返回0
        int leftDepth = getDepth(node -> left); // 递归求解左子树的深度
        int rightDepth = getDepth(node -> right); // 递归求解右子树的深度
        int Depth = 1 + max(leftDepth, rightDepth); // 计算当前节点的深度，即左右子树深度的最大值加1
        return Depth; // 返回当前节点的深度
    }

    // 用于计算二叉树的最大深度
    int maxDepth(TreeNode* root) {
        return getDepth(root); // 直接调用 getDepth 函数，返回二叉树的最大深度
    }
};


//递归法-前序遍历
class Solution {
public:
    int result; // 定义变量 result，用于记录二叉树的最大深度

    // 用于递归计算每个节点的深度
    void getDepth(TreeNode* node, int depth) {
        result = depth > result ? depth : result; // 计算当前节点到根节点的深度，并更新 result 值
        if (node->left == nullptr && node->right == nullptr) return ; // 如果当前节点为叶子节点，则返回
        if (node->left) { // 如果存在左子树
            getDepth(node->left, depth + 1); // 继续访问左子树，深度加1
        }
        if (node->right) { // 如果存在右子树
            getDepth(node->right, depth + 1); // 继续访问右子树，深度加1
        }
        return ;
    }

    // 用于计算二叉树的最大深度
    int maxDepth(TreeNode* root) {
        result = 0; // 将 result 变量初始化为 0
        if (root == nullptr) return result; // 如果二叉树为空，则直接返回 0
        getDepth(root, 1); // 递归计算二叉树的最大深度
        return result; // 返回二叉树的最大深度
    }
};


//迭代法-层序遍历
class Solution {
public:
    int maxDepth(TreeNode* root) { // 输入根节点指针，返回最大深度
        if (root == nullptr) return 0; // 特判：如果根节点为空，则返回0

        queue<TreeNode*> que; // 创建一个队列，储存每层的节点
        que.push(root); // 将根节点入队
        int depth = 0; // 初始化深度为0

        while (!que.empty()) { // 当队列不为空时，进行循环操作
            depth++; // 记录深度加1
            int level_size = que.size(); // 获取当前层的节点数
            for (int i = 0; i < level_size; i++) { // 遍历当前层的所有节点
                TreeNode* node = que.front(); // 取出队首节点
                que.pop(); // 队首节点出队
                if (node->left) que.push(node->left); // 如果有左子节点，加入队列
                if (node->right) que.push(node->right); // 如果有右子节点，加入队列
            }
        }
        return depth; // 返回最大深度
    }
};

递归的完整代码，供参考（来自AI）

#include<iostream>
#include<algorithm> //使用max函数需要头文件
using namespace std;

struct TreeNode{  //二叉树节点的结构体，包含val和左右子节点的指针
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x):val(x),left(NULL),right(NULL){}  //构造函数，用于创建新节点
};

int maxDepth(TreeNode* root){  //递归函数，返回二叉树的最大深度
    if(root==NULL) return 0;  //如果节点为空，则深度为0
    int leftDepth=maxDepth(root->left); //递归求解左子树的最大深度
    int rightDepth=maxDepth(root->right); //递归求解右子树的最大深度
    return max(leftDepth,rightDepth)+1; //返回左右子树深度的最大值加1
}

int main(){
    TreeNode* root=new TreeNode(1); //创建根节点
    root->left=new TreeNode(2); //创建左子节点
    root->right=new TreeNode(3); //创建右子节点
    root->left->left=new TreeNode(4); //创建左子节点的左子节点
    root->left->right=new TreeNode(5); //创建左子节点的右子节点
    cout<<maxDepth(root)<<endl; //输出最大深度
    return 0;
}

/*
根据题意，我们可以用递归的方法求解二叉树的最大深度。
定义递归函数maxDepth，输入参数为根节点root，输出为int类型，表示树的最大深度。
如果root为空，则深度为0，返回0。
否则，我们递归求解左右子树的最大深度，分别用leftDepth和rightDepth表示。
最终，树的最大深度等于左右子树深度的最大值加1，即max(leftDepth,rightDepth)+1。
最后在主函数中，我们创建一个二叉树，并输出其最大深度。
*/