线段树的构建

在了解线段树之前，我们先需要知道为什么需要线段树，构建线段树的意义是什么

线段树的意义

在解决区间问题的查询和修改时，通常会遇到查找和修改发生冲突的问题，想要快速查找，就必须选择不宜修改的存储方式，想要快速修改，就必须选择不宜查找的存储方式。

例：

对于数组arr=|1,2,3…n|来说,如果我们使用数组来存储每个元素，如果查询长度为m的区间的所有元素之和，就需要O(m)级别的时间来进行查询，如果要修改其中的一个值，就只需要花费O(1)级别的时间。

为了解决查询时间复杂度过高的问题，我们只需要计算出它的元素和数组就行，这样对于查询任何一个区段的元素之和，时间复杂度都变成了O(1)。

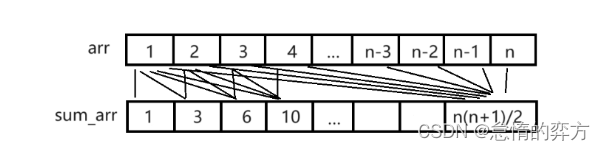
如果我们并不需要修改数组，这种做法就是完美的，但是，如果我们需要修改数组，我们就会发现更新sumarr的时间复杂度是O(n)。

就像一个天平一样，如果注重查询区间，那必然不易维护，如果注重修改，那必然不易查询区间。

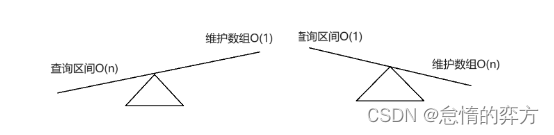
这个时候，有没有一种结构，可以让天平变得相对平衡呢？

线段树，就给出了解答。

线段树的构建

从零理解如何构建出线段树

对于元素和数组来说，我们可以将其看成由n个区间和组成的长度为n的数组。

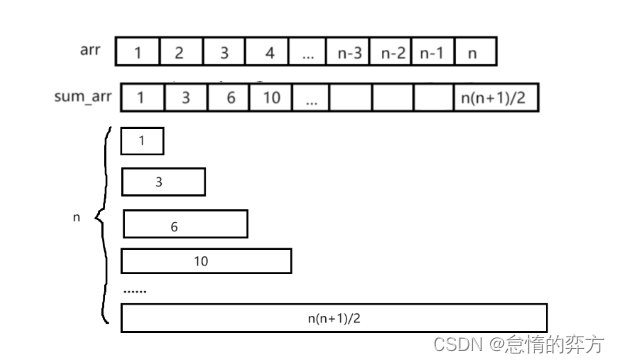
对此，就不难理解为什么维护元素和数组的时间复杂度这么高了。

那么，对于这个数组有什么方式可以改进呢？

对于O(n)，我们想要进一步优化的话就要优化成为O(log n)(O(1)在之前已经论证了是行不通的)，我们可以很容易联想到二分来进行优化。

例如对数组1,2,3,4,5,6,7,8,9,10

使用二分对区间进行划分，得到：

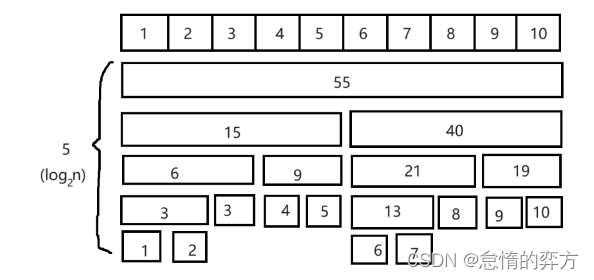
面对这样的区间划分，我们可以联想到什么？

对，二叉树。

使用二叉树的形式来存储我们使用二分划分后的区间。

对于一个长度为10的数组，我们使用二叉树的形式来进行存储

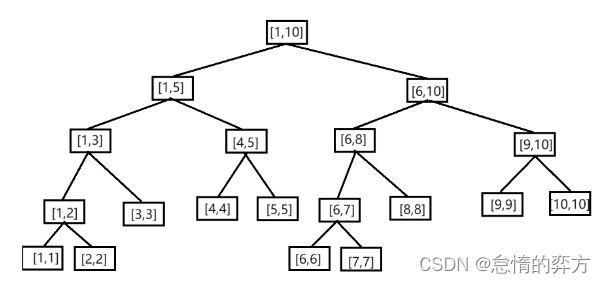
观察这颗二叉树，不难发现，如果去除最下面一层，这就是一颗满二叉树。

对于满二叉树来说，最适合的存储方式，就是顺序存储。所以，我们可以用顺序存储的二叉树来存储我们划分好的区间。

线段树的空间复杂度分析

节点数

对于长度为n的数列，对其进行二分区间划分，得到n+\frac{n}{2}+\frac{n}{4}+\frac{n}{8}+…+1个节点，约为2n(\leq2n)，所以空间复杂度为O(n)。

深度：

除去最后一层以外，可以看做满二叉树，所以深度depth为log_{2}(n-1)+1。

线段树的时间复杂度分析

对于查询操作：

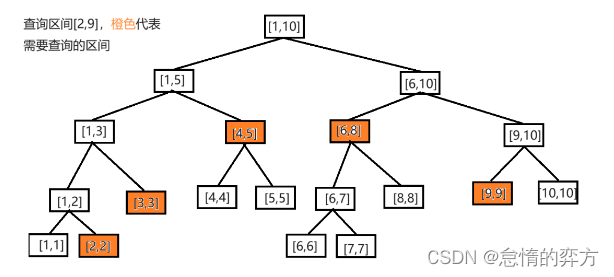
例如对于长度为10的线段树，我们查询最极限的情况，区间[1,9]之和，只需要查询[2,2],[3,3],[4,5],[6,8],[9,9]这五个区间。

对于查询区间[l,r]，我们最多沿着线段树从顶层走到底层两遍。例如对于最极限的情况，查询区间[2,n-1]，我们最多沿着线段树向下两次2×depth所以时间复杂度为O(log_{2}{n})。

图示：

对于修改操作：

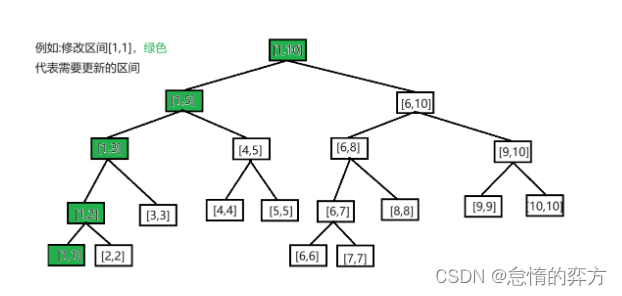
例如对于长度为10的线段树，我们修改[6,6]的值，需要更新的区间是[6,6],[6,7],[6,8],[6,10],[1,10]这五个区间。

对于查询区间[l,r]，我们最多沿着线段树从底层走到顶层一遍。例如对于最极限的情况，修改区间[1,1]，我们最多沿着线段树向上一次depth所以时间复杂度为O(log_{2}{n})。

图示：

构建线段树代码：

const int N;//N为数组长度
​
ll st[4 * N]{ 0 };//考虑极限情况，最后一层可能有2N个空位，所有要开4N大小的数组来存储线段树
​
void build(int l, int r, int p)//l为当前左边界，r为当前右边界,p为线段树当前编号
{
    //如果l和r相等，表示已经到了叶节点，直接返回。
    if (l == r)
    {
        st[p] = nums[l];
        return;
    }
    //二分递归建树
    int mid = (l + r) / 2;
    build(l, mid, p * 2);
    build(mid + 1, r, p * 2 + 1);
    st[p] = st[p * 2] + st[p * 2 + 1];//递归更新
}

线段树的操作：

1、查询区间和

ll getSum(int x, int y, int l, int r, int p)//x,y为待查询区间[x,y]的左右边界
{
    if (x <= l && r <= y)//如果当前节点被包含，直接返回当前节点的值
        return st[p];
    int mid = (l + r) / 2;
    ll sum = 0;
    if (x <= mid)//中间值大于等于左边界，表示左半界需要查询
        sum += getSum(x, y, l, mid, p * 2);
    if (mid < y)//中间值小于右边界，表示右边界需要查询，等于则表示没有右半界了
        sum += getSum(x, y, mid + 1, r, p * 2 + 1);
    return sum;
}
​

2、修改指定单点

void changeNode(int pos, int v, int l, int r, int p)//pos为目标位置，v为目标值
{
    if (l == r)
    {
        st[p] = v;
        return;
    }
    int mid = (l + r) / 2;
    if (pos <= mid)//pos在左子树
        changeNode(pos, v, l, mid, p * 2);
    else//pos在右子树
        changeNode(pos, v, mid + 1, r, p * 2 + 1);
    st[p] = st[p * 2] + st[p * 2 + 1];//递归回溯更新
}

3、修改指定区间

如果使用单点修改的方式，还不如模拟，所以需要使用延迟修改的方法。

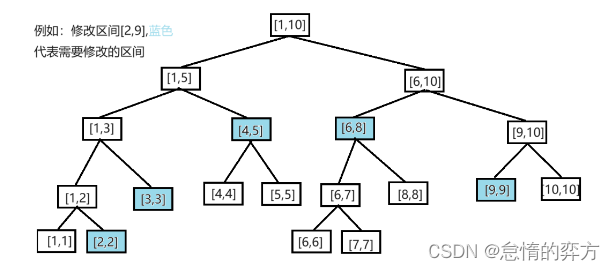
只要不查询[4,4],[4,4],[4,7],[8,8]就不对它们进行修改。

那怎么保证查询到[4,4],[4,4],[4,7],[8,8]时同时对它们进行修改呢？我们可以维护一个tag数组，表示当前节点含有延迟修改的值。

void checkDelay(int l, int r, int p)//检测函数，检查当前节点是否有延迟标记，有则传递给子树
{
    if (!tag[p])
        return;
    int mid = (l + r) / 2;
    tag[p * 2] = tag[p * 2 + 1] = tag[p];
    st[p * 2] = (mid - l + 1) * tag[p];
    st[p * 2 + 1] = (r - mid) * tag[p];
    tag[p] = 0;//清空tag
}
​
void changeInterval(int x, int y, int v, int l, int r, int p)//区间修改
{
    if (x <= l && r <= y)
    {
        tag[p] = v;
        st[p] = v * (r - l + 1);
        return;
    }
    checkDelay(l, r, p);//检测是否有延迟标记
    int mid = (l + r) / 2;
    if (x <= mid)
        changeInterval(x, y, v, l, mid, p * 2);
    if (mid < y)
        changeInterval(x, y, v, mid + 1, r, p * 2 + 1);
    st[p] = st[p * 2] + st[p * 2 + 1];
}

注：

如果使用了延迟修改的话，所有查询工作都需要加上延迟标记检测

4、指定区间加值

需要额外维护一个tag数组来表示乘法

//使用宏定义减少书写
#define ls p*2//左子树所在位置
#define rs p*2+1//右子树所在位置
#define mid (l+r)>>1
​
struct Node
{
    ll v;//区间和的值
    ll add;//加法tag
    ll mul;//减法tag
}sumST[4 * N];
​
void checkTag(int l, int r, int p)//要注意优先级的统一，这里设置的是加法优先结算和运算
{
    int m = mid;
    //更新区间和的值
    sumST[ls].v = (sumST[ls].v * sumST[p].mul + sumST[p].add * (m - l + 1));
    sumST[rs].v = (sumST[rs].v * sumST[p].mul + sumST[p].add * (r - m));
    
    //更新tag
    sumST[ls].mul = (sumST[ls].mul * sumST[p].mul);
    sumST[rs].mul = (sumST[rs].mul * sumST[p].mul);
    sumST[ls].add = (sumST[ls].add * sumST[p].mul + sumST[p].add);//注：这里代表加法优先结算，后面也需要同样先结算
    sumST[rs].add = (sumST[rs].add * sumST[p].mul + sumST[p].add);
    
    //清空tag
    sumST[p].mul = 1;
    sumST[p].add = 0;
}
​
void intervalMultiply(int x, int y, int k, int l, int r, int p)
{
    if (r < x || y < l)
        return;
    if (x <= l && r <= y)
    {
        sumST[p].mul = (sumST[p].mul * k);
        sumST[p].add = (sumST[p].add * k);//加法优先结算
        sumST[p].v = (sumST[p].v * k);
        return;
    }
    checkTag(l, r, p);
    int m = mid;
    if (x <= m)
        intervalMultiply(x, y, k, l, m, ls);
    if (mid < y)
        intervalMultiply(x, y, k, m + 1, r, rs);
    sumST[p].v = (sumST[ls].v + sumST[rs].v);//更新线段树
}

5、查询指定区间的最小值

我们就只要维护一个区间最小值的线段树就行

//建一个区间最小值的线段树
void buildMinNum(int l, int r, int p)//l为当前左边界，r为当前右边界,p为线段树当前节点的索引
{
    //如果l和r相等，表示已经到了叶节点，直接返回。
    if (l == r)
    {
        sum[p] = nums[l];
        return;
    }
    //二分递归建树
    int mid = (l + r) / 2;
    buildMinNum(l, mid, p * 2);
    buildMinNum(mid + 1, r, p * 2 + 1);
    sum[p] = min(sum[p * 2] , sum[p * 2 + 1]);//维护最小值
}
​
int getMin(int x, int y, int l, int r, int p)//x,y为待查询区间[x,y]的左右边界
{
    if (x <= l && r <= y)//如果当前节点被包含，直接返回当前节点的值
        return minNum[p];
    checkDelay(l, r, p);
    int mid = (l + r) / 2;
    int mn = 0;
    if (x <= mid)//中间值大于等于左边界，表示左半界需要查询
        mn = min(mn, getMin(x, y, l, mid, p * 2));
    if (mid < y)//中间值小于右边界，表示右边界需要查询，等于则表示没有右半界了
        mn = min(mn,getMin(x, y, mid + 1, r, p * 2 + 1));
    return mn;
}

总结

观察上面五种操作可以发现，线段树各种操作的核心在于递归更新和延迟检测，所有的操作都是基于这两个核心修改而来