目录
理解:

二分查找不是仅仅限于数组有序的情况能用,只要数组有一定的规律都行,后面讲解案例题的时候会说明,模板不要死记硬背,第一题是讲解朴素的二分模板,第二题是讲解另外两个的模板
例题讲解
leetcode704例题

算法原理讲解:
解法一:暴力枚举
从左往右依次对比每个数字,如果相等就返回
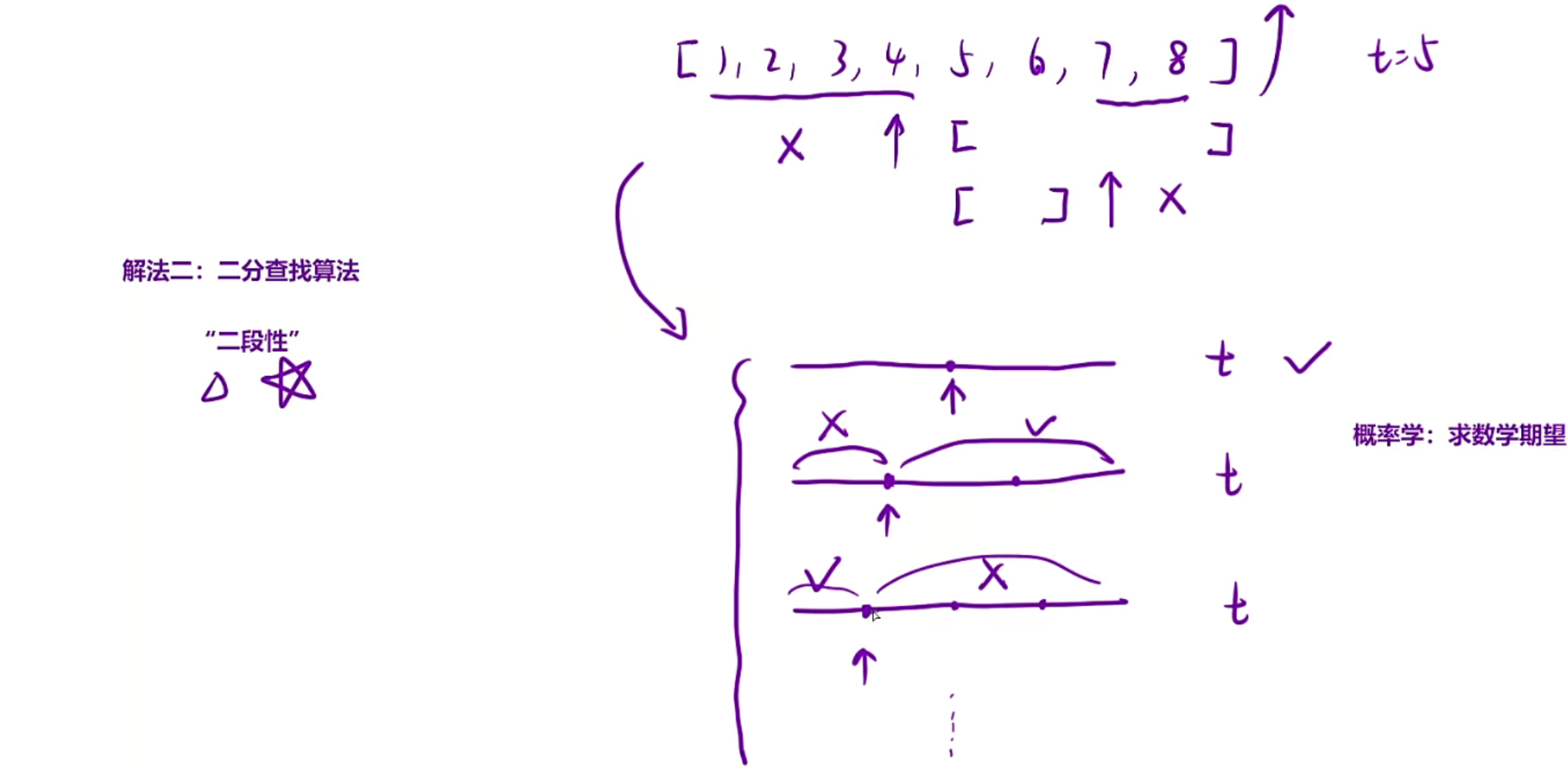
解法二:二分查找
当我们随便枚举一个数字比如4,会发现4和5比,4小于5,由于数组是升序,所以这里可以把4左边的区间全部排除掉,直接到【5,9】这个区间当中找,二分查找算法是利用了”二段性“,是因为我们寻找到一个规律,可以把数组分为两个部分,让其中的目标值在某一部分,直接能够排除掉另外一部分,在其中我们的切分点可以是二分之一,也可以是五分之一,四分之一,但是为什么选择二分之一,这是概率学中的数学期望问题,严格证明的话二分点是最优解
注意:我们这里不提及有序性,只要有”二段性“,也就是之前理解部分我们说的有一定规律就可以用二分查找
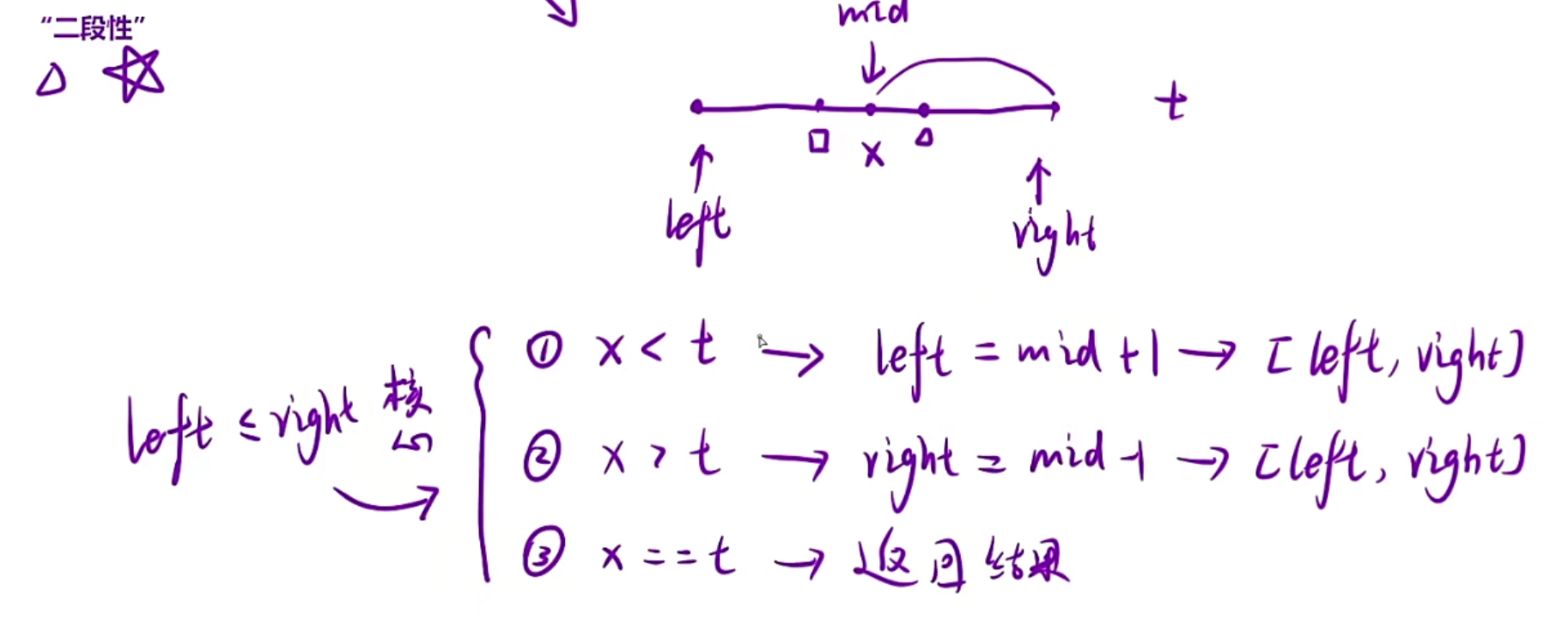
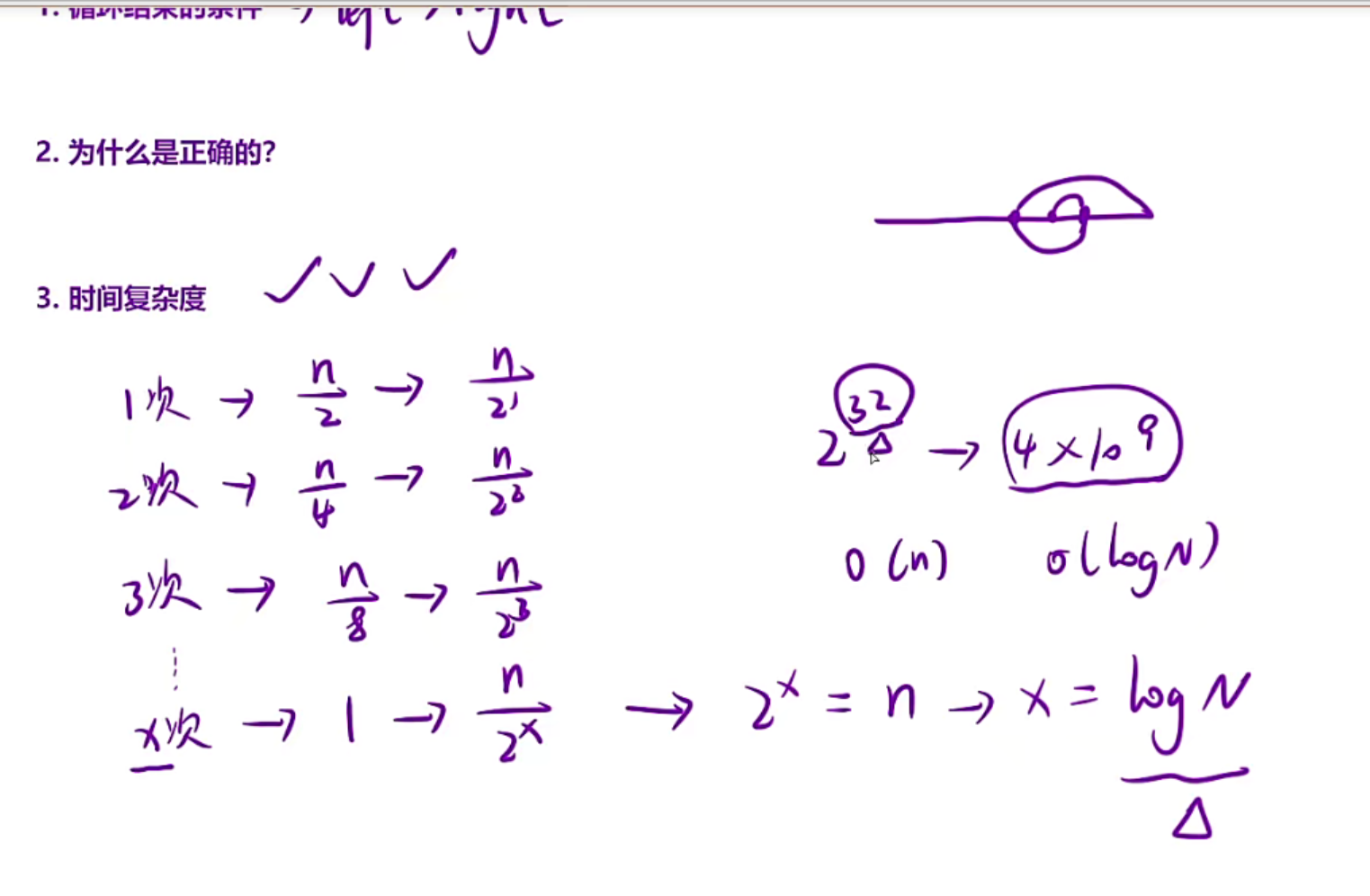
当left>right的时候循环结束
时间复杂度为logN,这是一个非常优秀的算法
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0, right = nums.size()-1;
int mid;
while (left <= right) {
mid = (left + right) / 2;
//为了防止溢出,可以left+(right-left)/2
//这里/2 /3 /4 都是可以的,看你选择几分点
if (nums[mid] > target)
right = mid - 1;
else if (nums[mid] < target)
left = mid + 1;
else
return mid;
}
return -1;
}
};注意:这里是left<=right进入循环,还有righ是等于右边结点下标,所以是size-1,如果是size就错
这里选择二分点是最优的
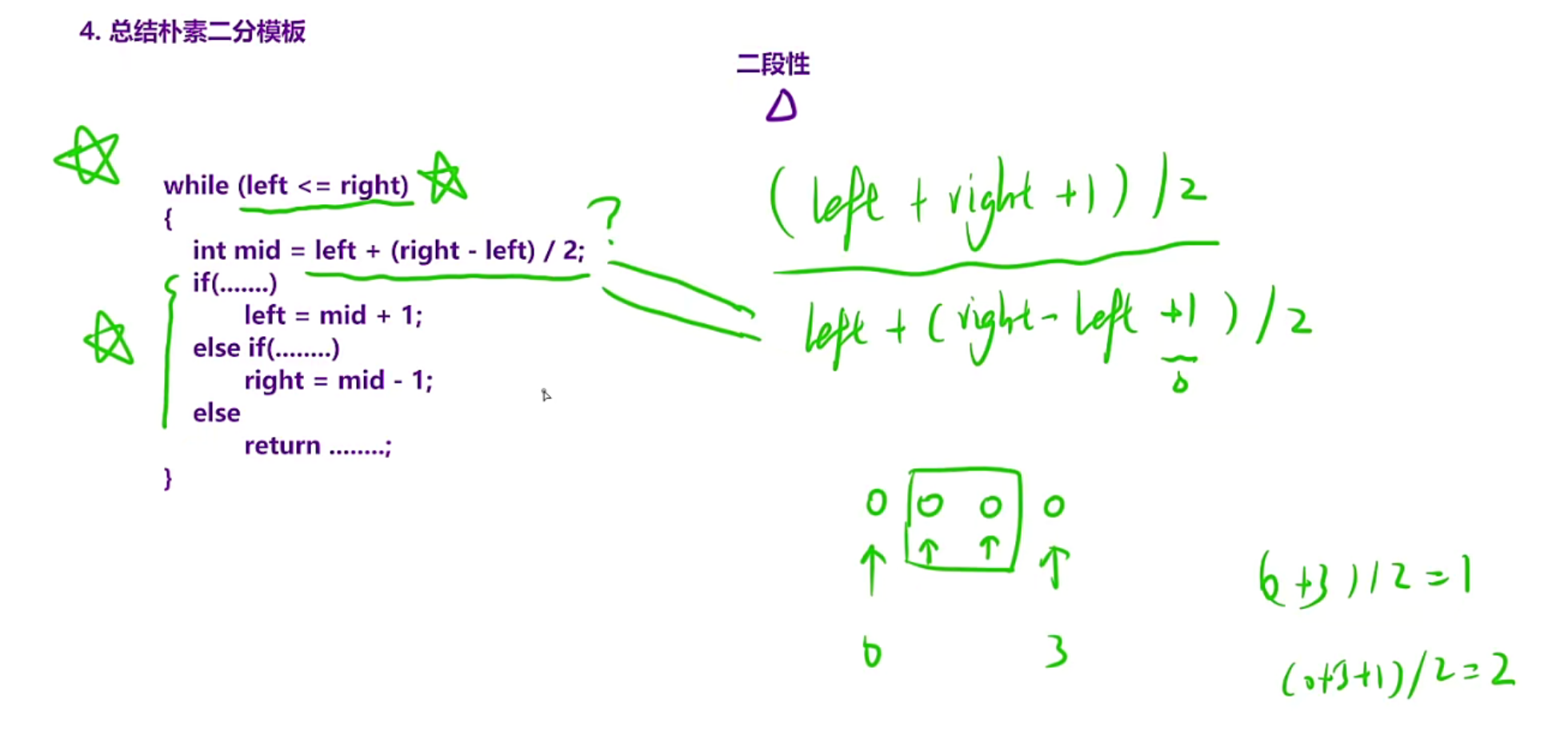
模板注意
1.left<=right进入循环
2.防溢出的处理,右边绿色是说明+1有没有区别,如果对于防溢出,不+1就是当偶数的时候求的是中间偏左边的位置,+1就是求中间偏右边的位置
3.if里面的条件判断根据二段性来填写
leetcode34例题


解法一:暴力解法,时间复杂度O(N)
解法二:朴素二分,也就是找到一个目标值的时候,在往左边和右边一直找,直到找到起点和终点,但是当特殊情况的时候,时间复杂度就会降为O(N),所以也不是最优解
解法三:利用二段性,查找区间的左端点/右端点
查找左端点
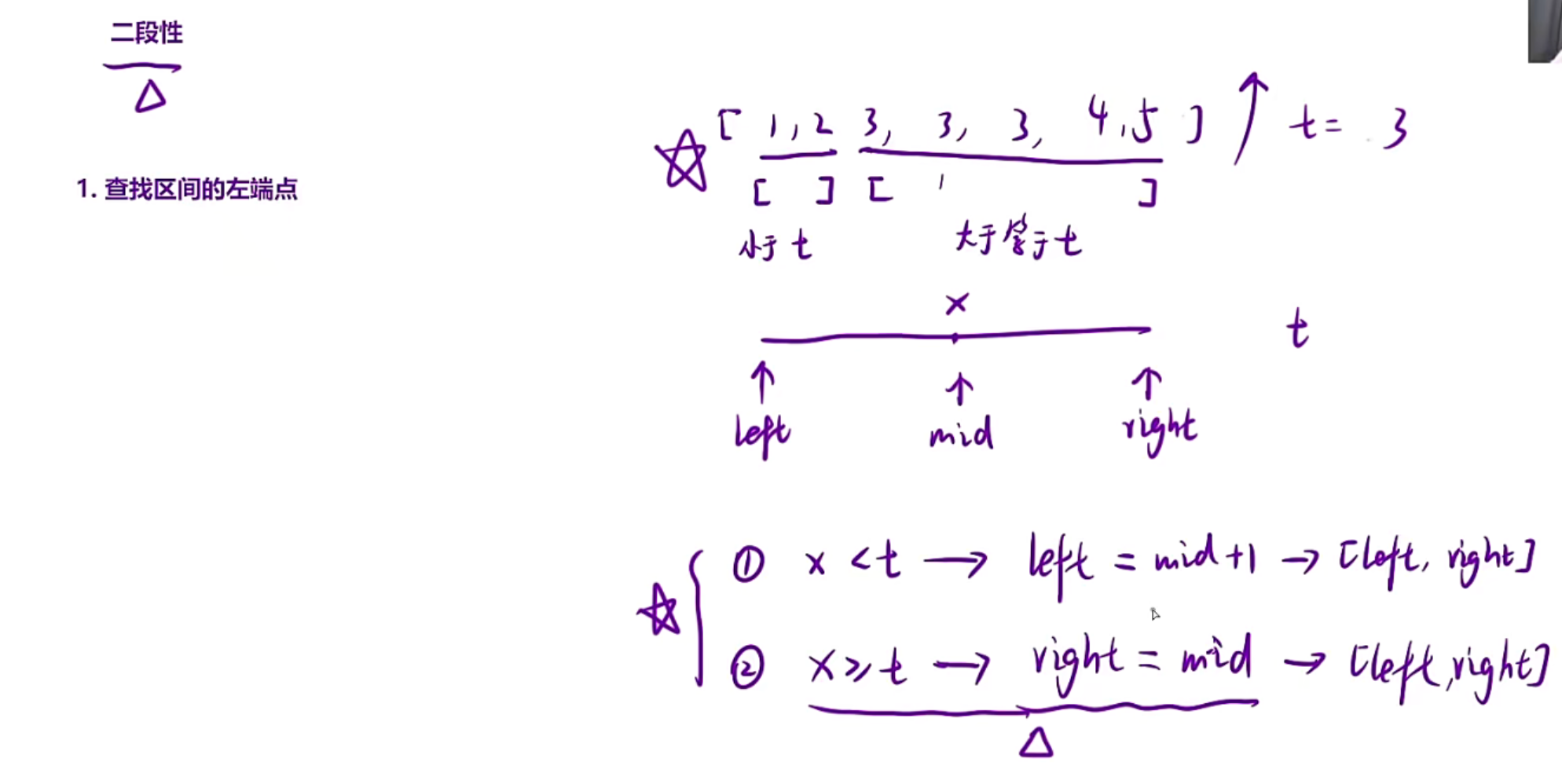
先看上图的右边部分,假设数组为{1,2,3,3,3,4,5},target为3,那寻找左端点就是第一个3,如何寻找?(下标为mid的值为x)
当x<t的时候,说明mid左边包括mid都是小于t的,右边都是>=t的,所以此时分为两边,那左端点肯定是在右边,比如这里的数组分为{1,2},{3,3,3,4,5},所以此处的操作是left=mid+1;
当x>=t的时候,说明【mid,right】区间都是>=target的,但是mid也不一定是左端点,也可能是左端点,所以此时我们要缩小右边,让right=mid,right不能=mid-1,因为mid可能就是左端点,如果你right=mid-1,就会错过左端点
思考:为什么不是分成3种,> = <,而是两种< >=?
这是和朴素二分不一样的地方,因为如果你不是>=的话,你等于的那个点都不是最终的要找的点
难点在于细节操作
1.循环条件(left<=right? left<right?)
2.求中点的操作

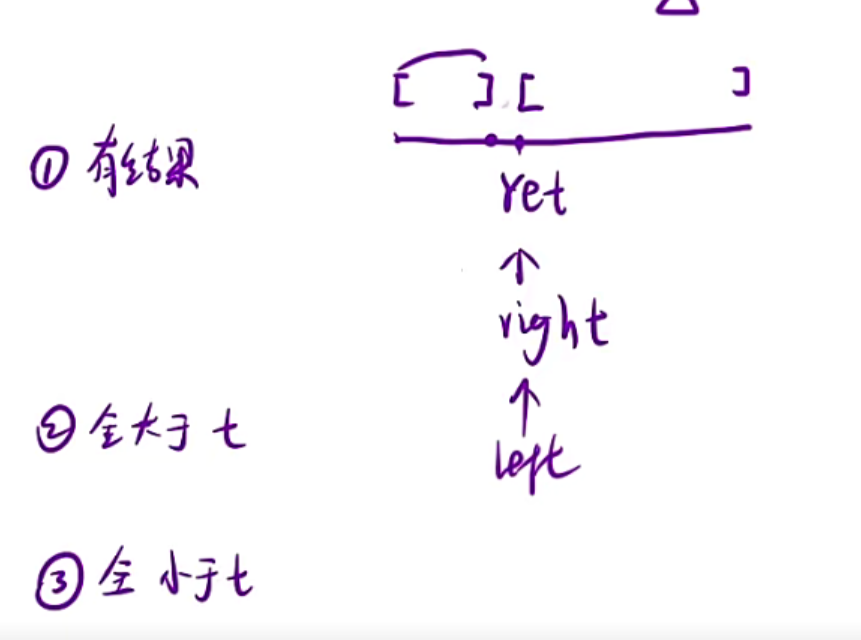
比如这里的第一种情况,通过上面的分析,我们发现left是始终在一个<target的区间跳跃并且一直想要跳出这个区间然后到左端点,right是始终在>=的区间跳跃,始终不会跳到左边,所以最后一步就是right指向左端点,然后left跳一步到左端点,那此时left和right相等并且指向左端点(无论最后怎么样,你都是left和right相等指向左端点)如果你此时循环条件是left<=right,那就会在循环一次,right=mid,然后求中点,一直right=mid,就会进入死循环,所以循环条件应该是left<right,此时最后一下left=right跳出循环,此时的点就是左端点
对于第二第三种情况很好分析,全大于t,那就是right一直左移一直左移,left不动

之前做朴素二分的时候,+1和不加1都是可以得出结果的,但是这里不是
+1和不加的区别就是区间是偶数个的时候,不加1就是求的中间的两个偏左边的,+1就是求的中间的两个的偏右边的
特殊情况就是当数组的元素只有两个的时候,+1就会求到右边,mid=右边那个,如果mid的值<t,那left=mid+1,循环结束,是正确的
但是如果你的mid的值>=t,那right=mid,就会一直计算,一直死循环
所以我们求中点的时候不要采用+1的写法
查找区间右端点
这里也是利用二段性:将数组分为两个区间,小于等于和大于

class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
if(nums.size()==0){
return {-1,-1};
}
vector<int> ret;
//寻找区间左端点
int left=0,right=nums.size()-1;
int mid=-1;
while(left<right){
mid=left+(right-left)/2; //防止溢出并且不+1
if(nums[mid]<target){
left=mid+1;
}
else{
right=mid;
}
}
if(nums[left]==target){
ret.push_back(left);
}
else{
return {-1,-1};
}
//寻找区间右端点
left=0,right=nums.size()-1;
while(left<right){
mid=left+(right-left+1)/2; //防止溢出并且+1
if(nums[mid]<=target){
left=mid;
}
else{
right=mid-1;
}
}
if(nums[right]==target){
ret.push_back(right);
}
return ret;
}
};
注意:要在理解算法原理的基础上再去记忆模板,而且模板不需要特别的去记,因为我们知道算法原理,所以可以推导,并且要注意细节的处理,细节处理反而更重要
leetcode69例题

算法原理讲解:
解法一:暴力解法
当一个数x的时候,我们可以从1进行枚举,1的平方=1,看和x比较,如果小于,那就2的平方
一直到n的平方,这个n的平方可以是等于x,也可以是小于x,但是n+1必须大于x
解法二:二分查找
在区间【1,x】中寻找一个数,使得这个数的平方和满足题意
利用二段性,我们发现,区间可以分为两段,左边是<=,右边是>
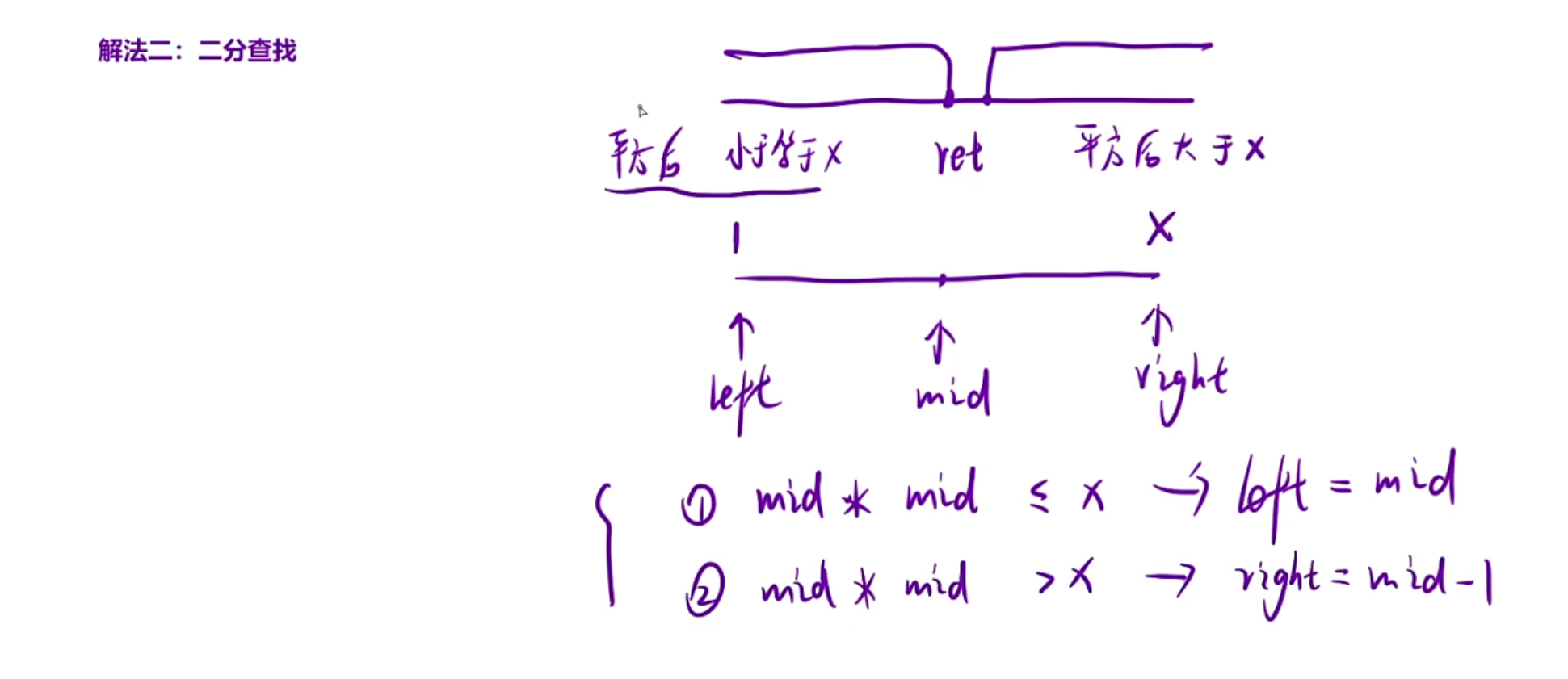
通过前面两道题的解法,我们发现可以很快速的写出left和right是如何移动的,此时只要注意循环结束条件和mid的求法即可,由于是right=mid-1,所以mid在解的时候要+1求右边哪个,否则没有+1的话就会求左边的,可能导致进入死循环
循环结束返回left即可
class Solution {
public:
int mySqrt(int x) {
if(x<1)return 0;//处理边界情况
//二分查找
int left=1;
int right=x;
long long mid;
while(left<right){
mid=left+(right-left+1)/2;
if(mid*mid<=x){
left=mid;
}
else{
right=mid-1;
}
}
return left;
}
};leetcode35例题

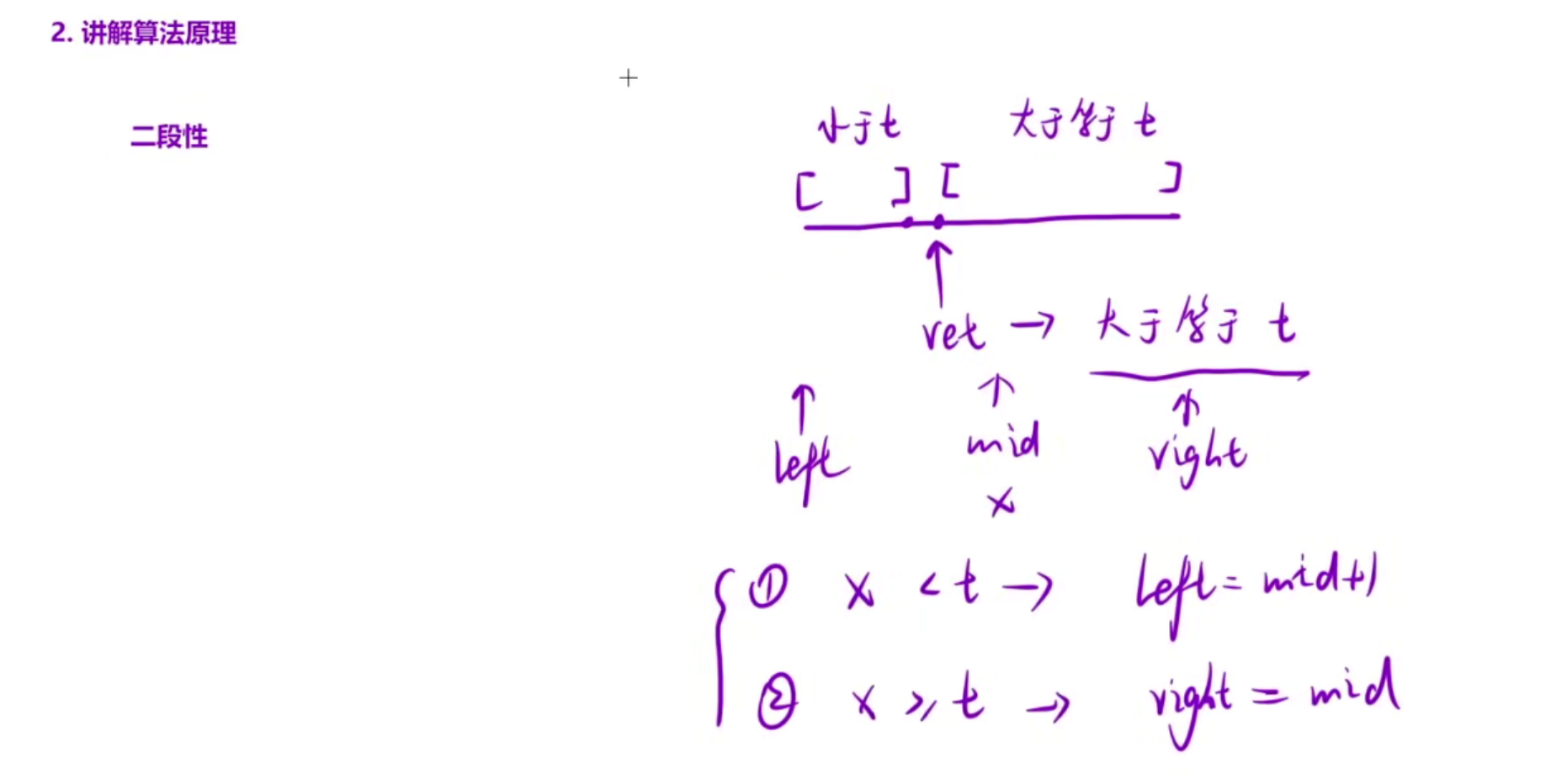
算法原理讲解:
二分查找:二段性
看一下能否把数组根据规律划分为两个区间
看示例,我们发现插入的位置是第一个比target大的前面或者返回和target相等的位置
此时我们就可以把数组分为两部分,左边小于,右边大于等于,然后插入的位置就是右边的第一个位置,然后写出left和right是怎么移动的,然后注意细节问题就行,最后返回left就行,因为left最后肯定是执行>=的位置,但是这里要处理一下边界,如果数组全部都小于的话,那left就会一直往右边移动,此时==right结束,但是插入位置应该在最后一个元素的后面
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
//寻找左端点
int left=0;
int right=nums.size()-1;
int mid;
while(left<right){
mid=left+(right-left)/2;
if(nums[mid]<target){
left=mid+1;
}
else{
right=mid;
}
}
if(nums[left]<target)
return left+1;
return left;
}
};leetcode852例题

算法原理讲解:
一、暴力解法
用一个指针指向开始的位置,然后依次找,如果arr[left]<arr[left+1],那left++
如果找到下一个位置比当前位置小,说明是峰值,返回即可
时间复杂度O(N)
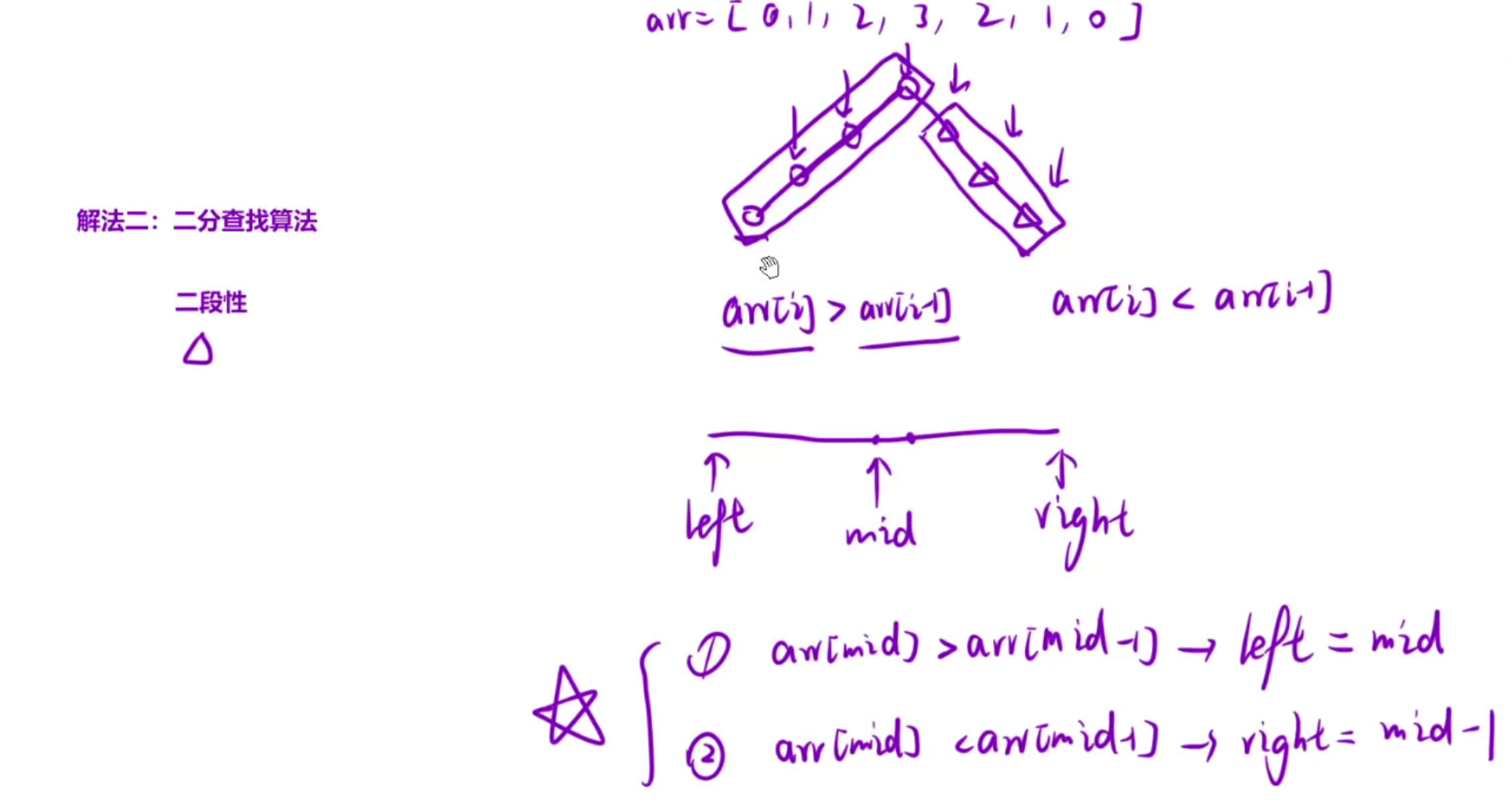
二、二分查找:利用二段性
我们发现这个数组被峰值分为两边,左边arr[i]>arr[i-1],右边arr[i]<arr[i-1]
所以我们只需要比较一些找到的mid的位置的前一个比较一些,然后移动left和right即可
class Solution {
public:
int peakIndexInMountainArray(vector<int>& arr) {
int left=0;
int right=arr.size()-1;
int mid;
while(left<right){
mid=left+(right-left+1)/2;
if(arr[mid]>arr[mid-1]) left=mid;
else right=mid-1;
}
return right;
}
};注意这里left=mid,是因为mid这个位置可能就是峰值,所以不要越过去,但是right就不是峰值,所以可以越过,看你怎么划分,是把峰值划为左边还是右边
class Solution {
public:
int peakIndexInMountainArray(vector<int>& arr) {
int left=0;
int right=arr.size()-1;
int mid;
while(left<right){
mid=left+(right-left)/2;
if(arr[mid]>arr[mid+1]) right=mid;
else left=mid+1;
}
return left;
}
};这种写法就是把峰值划为右边,所以看你怎么划分你的数组
leetcode162例题

算法原理讲解:和上一道题一样的,因为题目只要求你返回其中一个就行
class Solution {
public:
int findPeakElement(vector<int>& nums) {
int left=0;
int right=nums.size()-1;
int mid;
while(left<right){
mid=left+(right-left+1)/2;
if(nums[mid]>nums[mid-1]) left=mid;
else right=mid-1;
}
return left;
}
};如果想要彻底搞懂

这是三种峰值的情况,因为题目有说-1的位置为负无穷,所以如果你0位置之后递减,说明0这个位置就是峰值
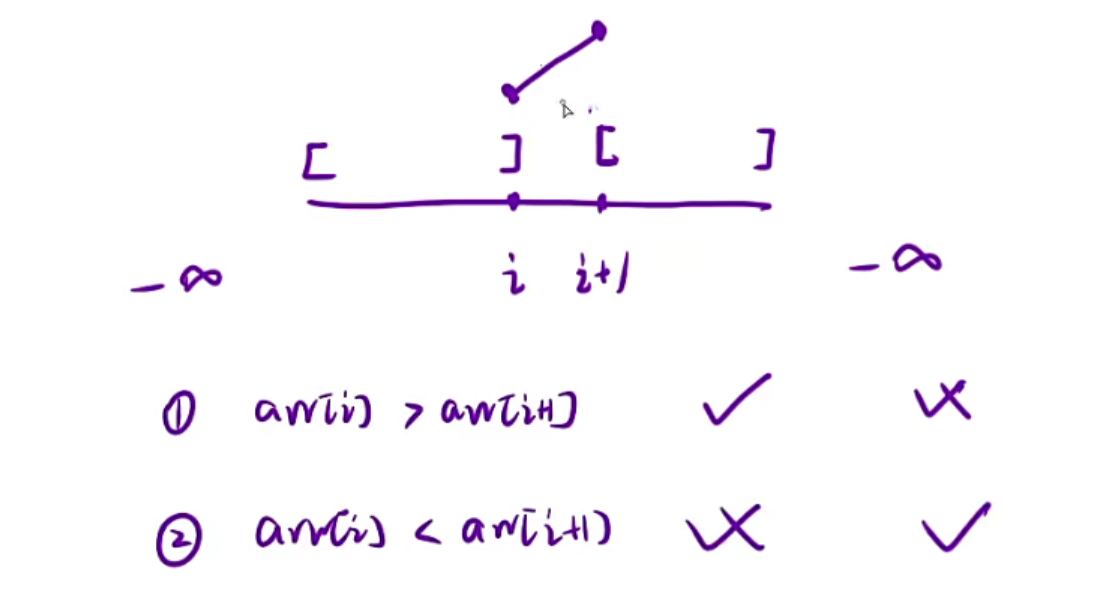
假设我是arr[i]<arr[i+1],那此时右边是一定会有峰值的,因为你前面和后面都是负无穷,你在这里上升了,右边是负无穷,所以右边是一定会有峰值的,但是左边不是,左边看你一直上升不一定有峰值,所以最好的办法就是去右边去找
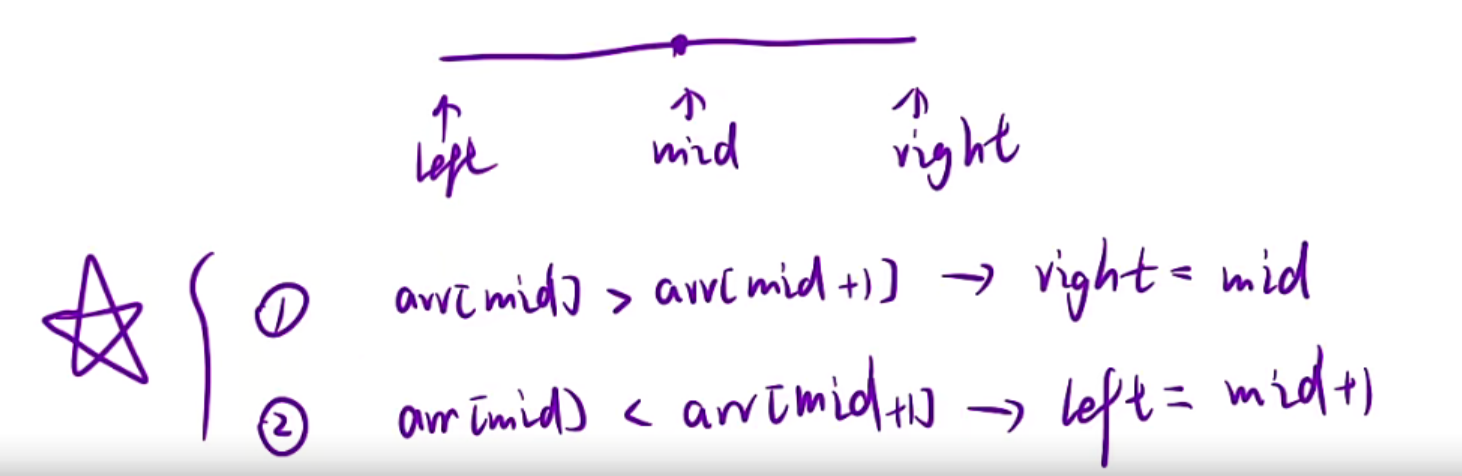

代码和我们之前上面那个是一样的,只是我们换了另一种角度去理解代码而已
leetcode153例题

算法原理讲解:
一、暴力解法,也就是一个一个比,谁小就返回谁,但是时间复杂度为O(N)
二、二分查找
注意读题:每个元素都不一样,比如{3,4,5,1,2},1的左边的最小是3,都比右边最大的2大
所以数组可以被分成两部分,{3,4,5} {1,2},两边都是严格递增的
所以我们这里把1划分为右边,现在寻找mid变换,left和right怎么变换
如果mid位于数组左边,也就是nums[mid]>=nums[0],left=mid+1,因为mid这个位置也不可能是最终答案
如果mid位于数组右边,也就是nums[mid]<nums[0],right=mid,因为mid这个位置可能是最小值,所以不要越过mid
然后注意一下特殊情况,也就是旋转多次之后回到原来样子,也就是示例3
class Solution {
public:
int findMin(vector<int>& nums) {
int left=0;
int right=nums.size()-1;
if(nums[left]<nums[right])
{
return nums[left];
}
int mid;
while(left<right){
mid=left+(right-left)/2;
if(nums[mid]>=nums[0]) left=mid+1;
else right=mid;
}
return nums[right];
}
};注意:这里是选择nums[0]作为参照,所以边界情况要处理,但是如果你以nums[size()-1]作为参照的话就不需要处理边界情况,因为你的right一直左移,但是如果以0作为参照的话对于一直递增要特殊处理
剑指offer53
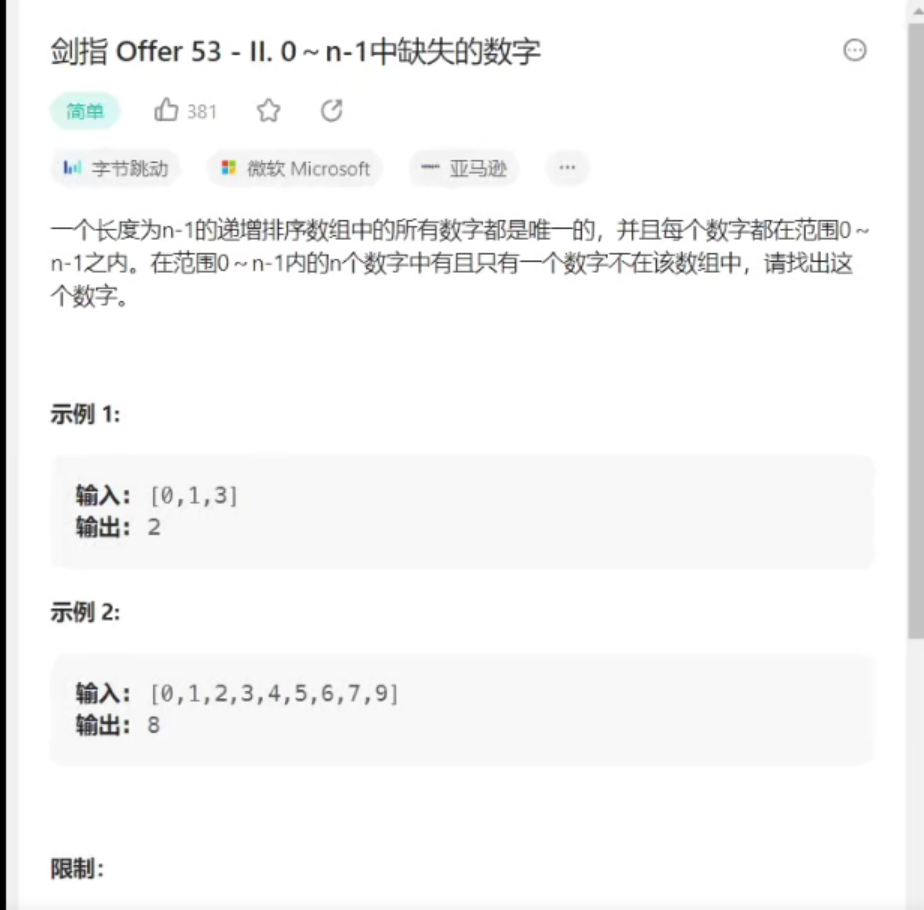
面试当中可能会给一道简单题,让你发散思维看看你有没有多种解法,能不能再优化

二段性很难找
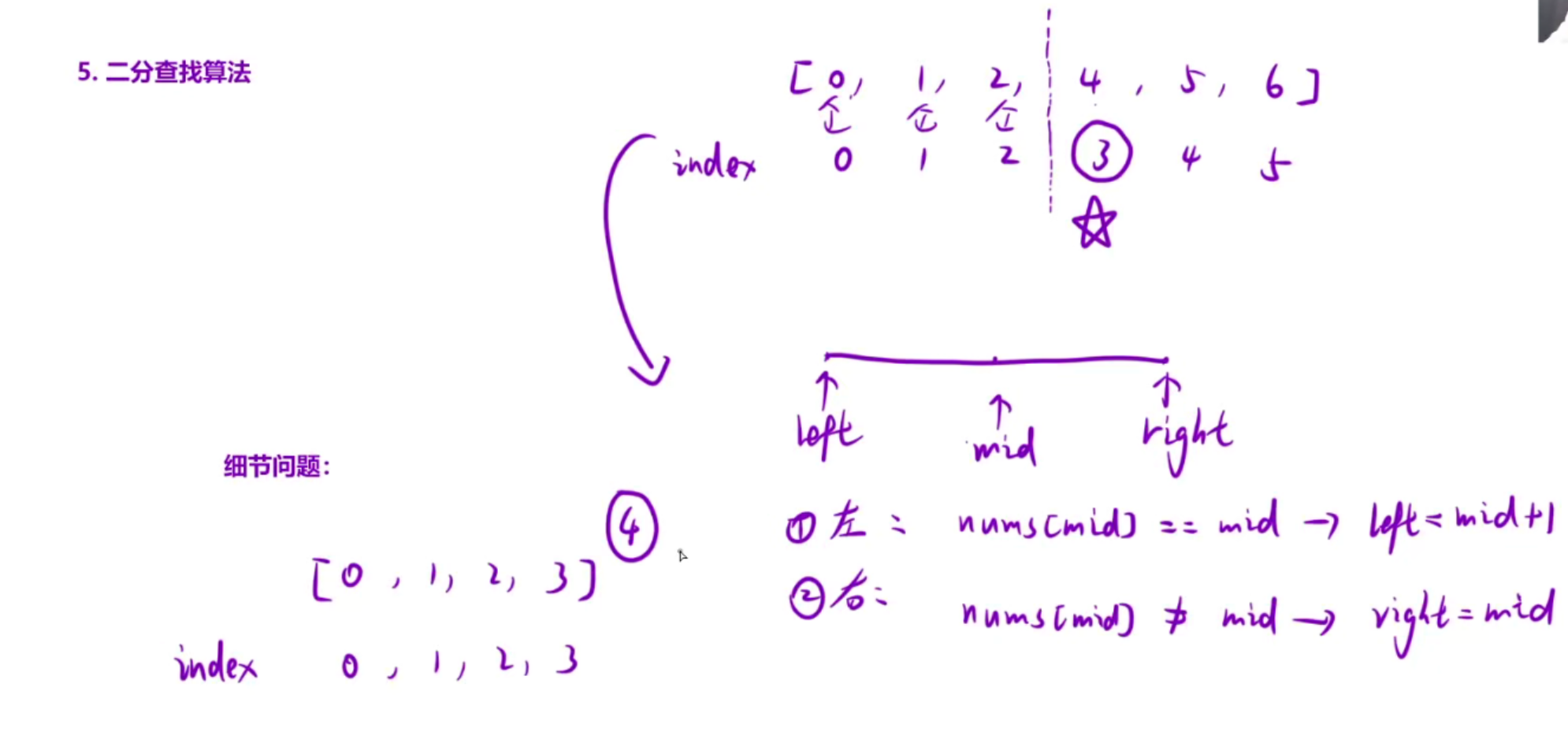
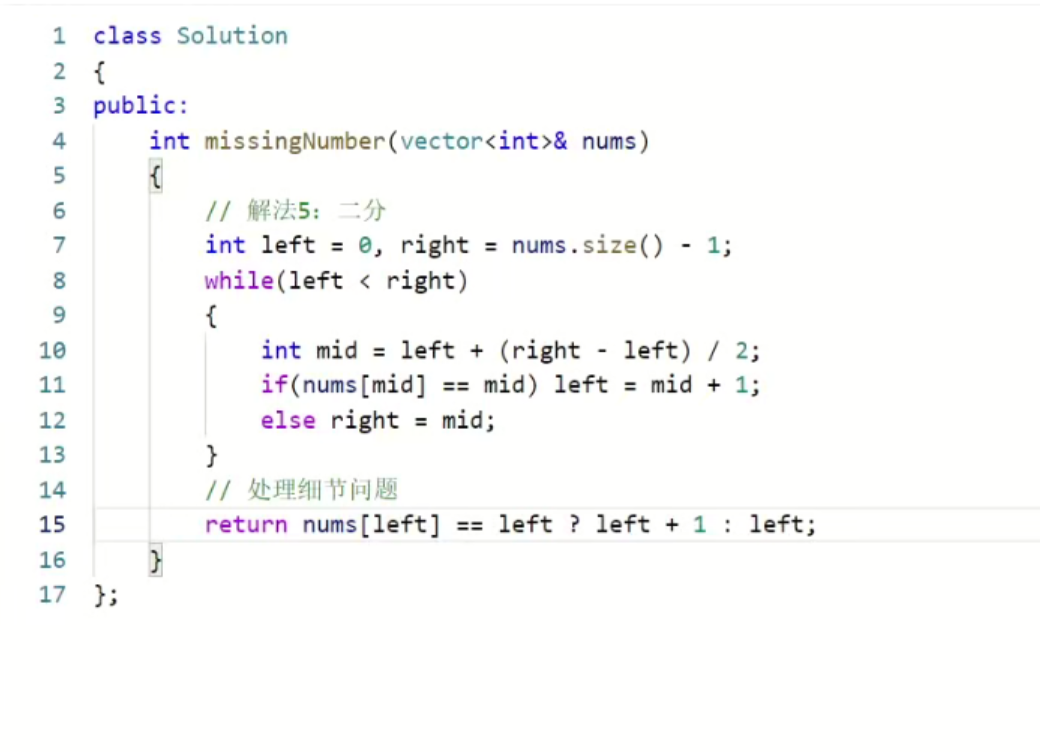
总结:
二分查找是利用数组的二段性,而不是仅仅针对于有序数组
对于循环结束条件,mid计算时+1还是不+1,mid计算时需要防止溢出风险
left和right的移动策略
返回值






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








