位运算全解析：从入门到精通

最新推荐文章于 2025-12-08 20:31:24 发布

原创最新推荐文章于 2025-12-08 20:31:24 发布 · 988 阅读

26 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #位运算

优选算法精品专栏收录该内容

8 篇文章

订阅专栏

常见的位运算

&按位与：两个位都为 1 时，结果为 1；否则为 0。记忆方法：有0则0，就是平时的逻辑运算的&&只有两个都为真的时候才能出1

|按位或：两个位中至少有一个为 1 时，结果为 1；否则为 0。记忆方法：有1则1，就是平时的逻辑运算的||，有一个真就出1

^按位异或：两个位不同时为 1，相同时为 0。记忆方法：相同为0，相异为1 / 无进位相加，这两种方法最好都记一下

异或异或就是相异为1

无进位相加比如0^0 类比二进制的0+0=0所以结果为0

1^1 =1+1=10，但是不看进位不进位，看最低位即可，所以为0

1^0=1+0=1，所以结果为1

综上：

按位与：有0则0

按位或：有1则1

按位异或：相异为1 / 无进位相加（只看本位）

<<左移：将二进制位向左移动 n 位，高位丢弃，低位补 0。相当于*2，因为是二进制

比如3<<2，011<<2，1100=12，3*2*2=12

注意：对负数进行左移会出错

>>右移：

无符号：逻辑右移，高位补 0

有符号：算术右移，高位补符号位（正数补 0，负数补 1）

相当于除2，因为是二进制

比如8>>2，1000>>2，0010=2，8/2/2=2

~按位取反：将位 0 转为 1，1 转为 0（单目运算符）。

比如对~3 3的原反补码相同，00000011，然后按位取反，11111100（这是补码）减一变成反码

11111011，符号位不变，按位取反，10000100，此时就是-4 ~x=-(x+1) ~3=-(3+1)=-4

注意：左移就是往高位移，右移就是往低位移

优先级：~ >> / << & ^ | (这里能加括号就尽量加括号，也方便阅读)

基础常见位运算题型

在这里我们做一下统一：全部从低位到高位，下标从0开始，所以对于32位来说，下标最大为31

这样做的好处是，如果右移多少位即下标，比如00100，1的下标为2，1右移两位就是下标

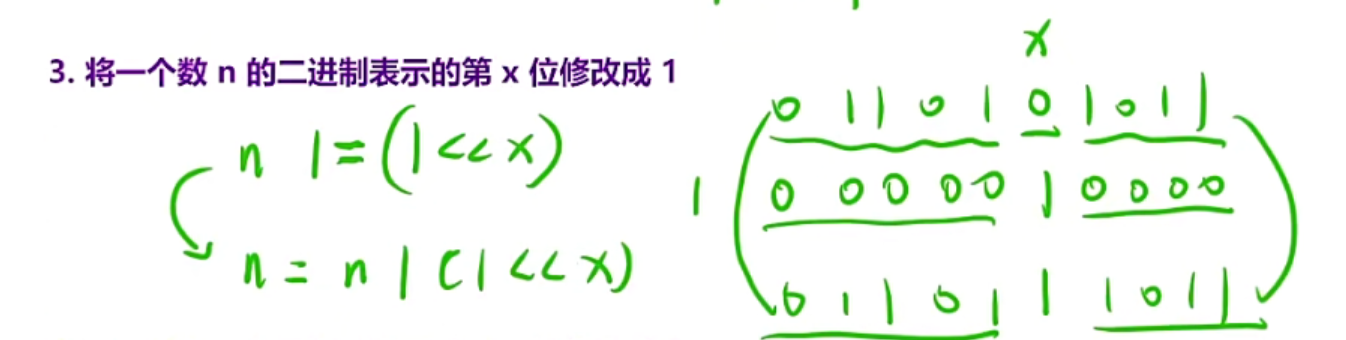
第二第三第四题是一类问题：是用于为位图做服务的

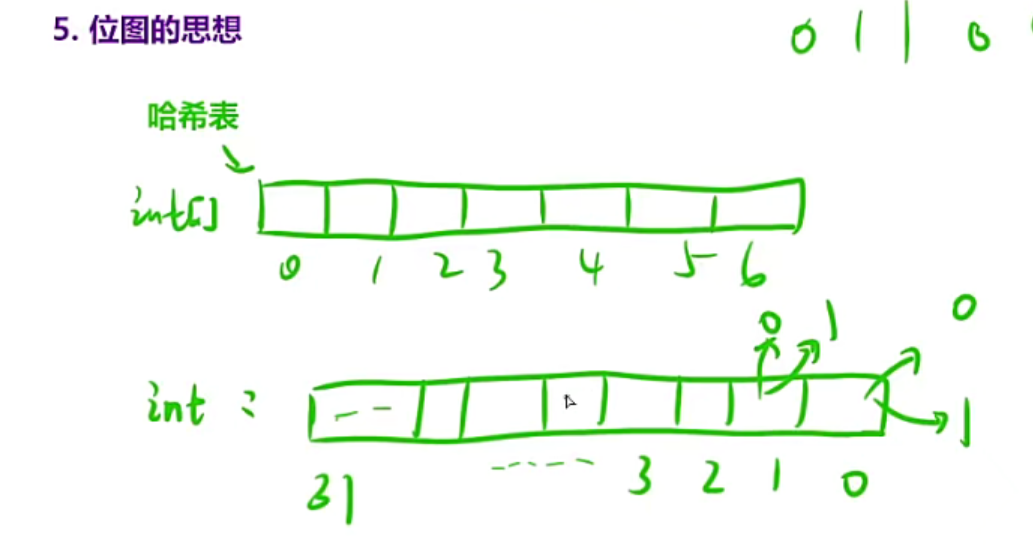
位图的思想本质就是一个哈希表，只不过哈希是一个数组，但是位图使用bit位，比如之前如果存32个东西，你可能采用32个int，但是位图只需要1个int，32个bit位来表示，题234就是为位图服务的，因为我们有时候要知道位图当中某个位是0还是1，想要修改成0还是1

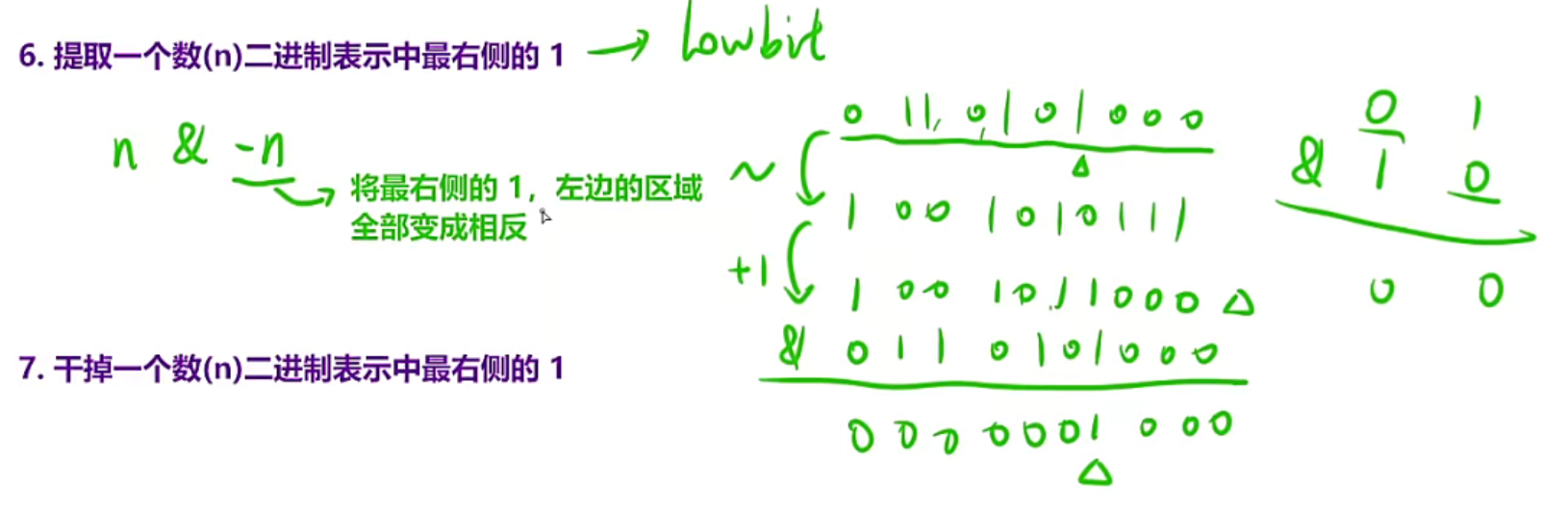
第六题可以叫做lowbit操作：也就是提取最右侧的1，首先看-n，-n就是就的话就跟原来的n按位取反然后+1，此时发现最右侧的1，左边的区域全部取反，但是右边的区域不变

然后再按位与，因为左边的区域反了按位与就会变成0，但是右边全是0，也不变，按位与之后还是0，所以这样只会留下一个最右侧的1，所以操作就是n&-n

第七题：n-1，因为最右侧的1的右边全是0，所以你-1就会导致他们需要借位，这样就导致右边变成011，所以全都反了过来，导致1的左侧不变，右侧包括1变成了01111……

所以再进行按位与即可

第6和第7题是可以解决leetcode191和338例题和461例题的，可以自己去尝试一下

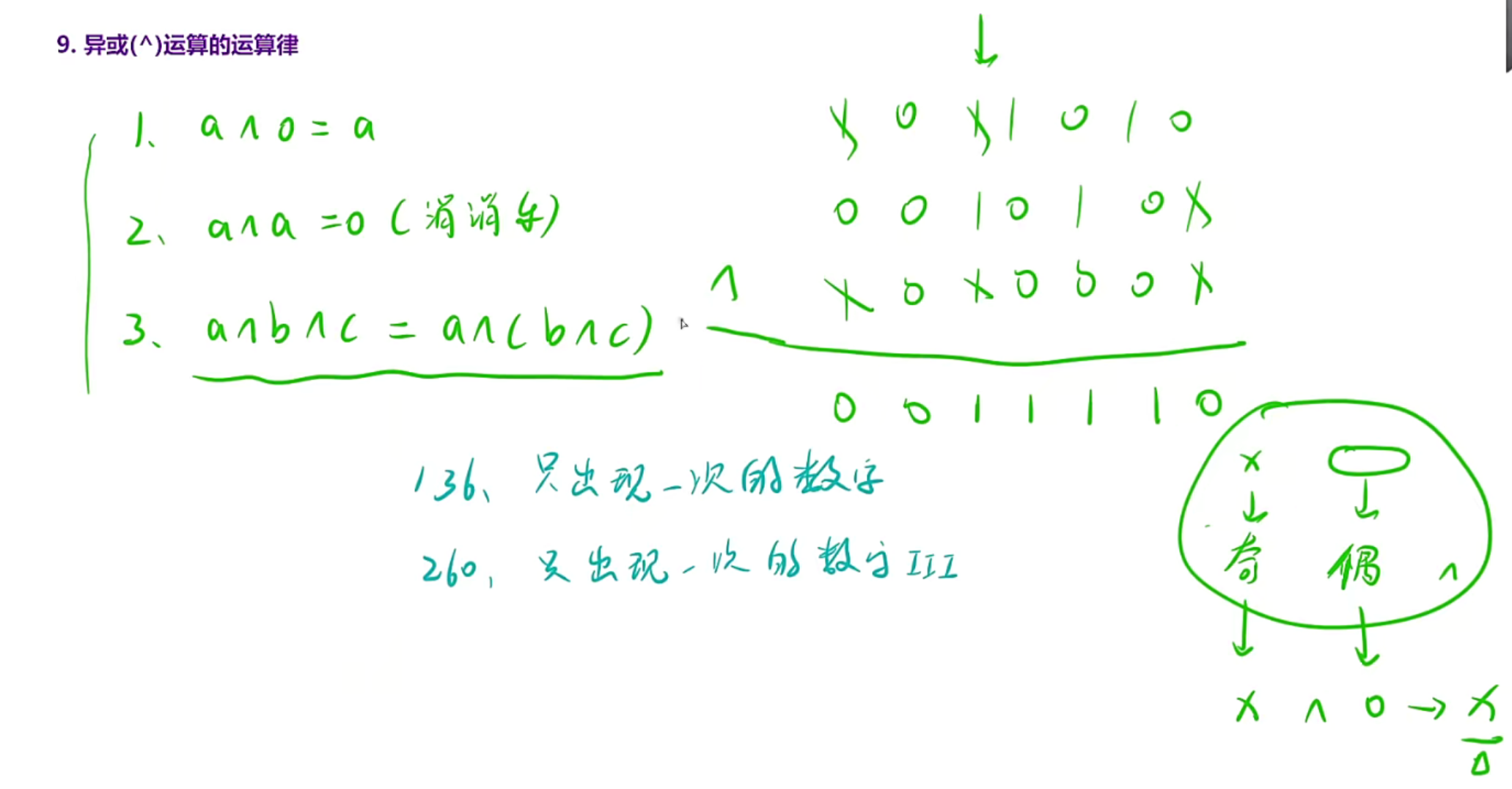
只要清楚异或是相异为0，和无进位相加即可，123都很好证明，可以自行证明

这里需要注意的是第三点，也就是你一堆数，无论谁和谁先异或都无所谓，不讲究顺序，所以可以利用第一点和第二点，两个相同的异或就会出0，这样就可以消掉重复的数字，如果一个数字和0异或还是本身

leetcode136和260例题可以自己做一些

例题

leetcode面试0101

算法原理讲解：

一、哈希表：时间复杂度O（N），空间复杂度O（N），由于都是小写字母，可以开一个hash[26]，空间复杂度O（1）

二、用位图记录，1表示存在，0表示没有

细节就是对应关系，因为a为97，所以一开始算的时候要对应到位图的0位，所以要-97

优化点：鸽巢原理：如果字符串大于26个，肯定有一个重复的，所以可以返回false

class Solution {
public:
    bool isUnique(string astr) {
        if(astr.size()>26) return false;
        int bit=0;
        for(int i=0;i<astr.size();i++){
            int a=(int)astr[i]-97;
            if((bit>>a)&1){
                return false;
            }
            bit|=1<<a;
        }
        return true;
    }
};

leetcode268例题

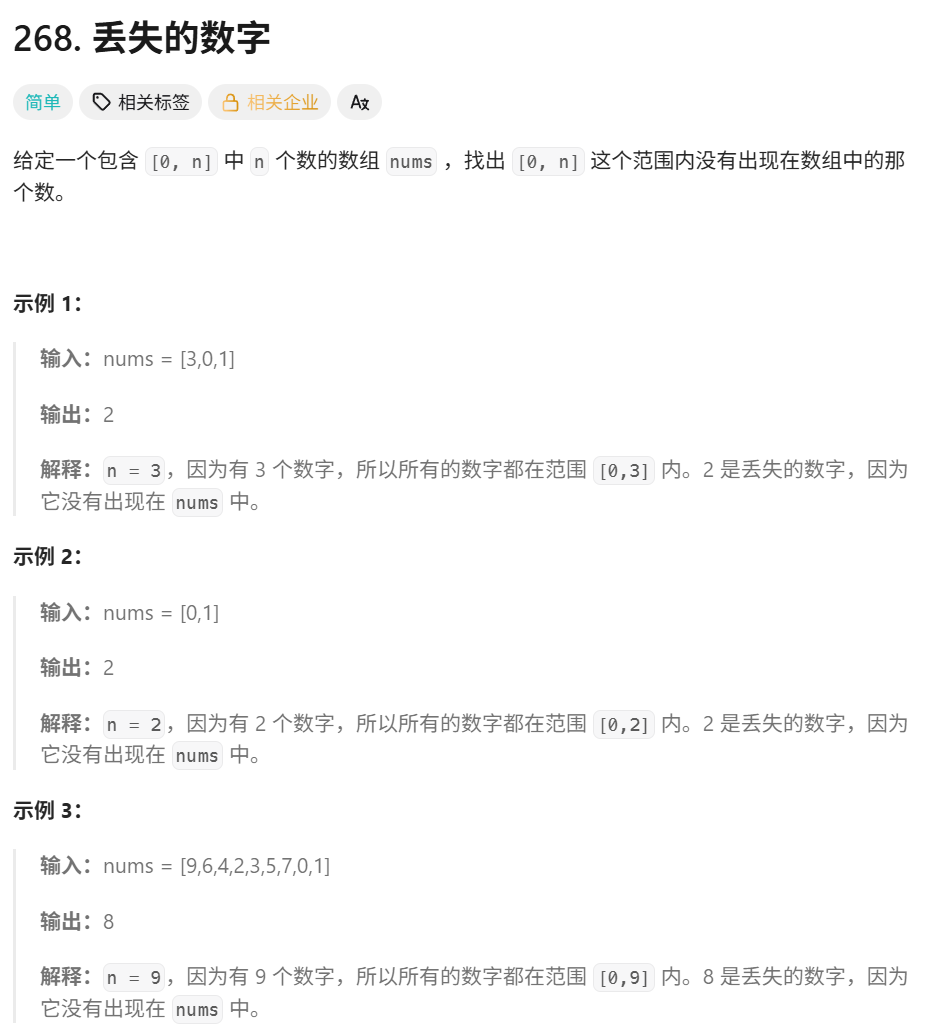
算法原理讲解：

一、哈希表

二、高斯求和

三、异或运算（直接让数组和0-n的每个数的异或，剩下的就是没出现的）

class Solution {
public:
    int missingNumber(vector<int>& nums) {
        int n=nums.size();
        int sum=0;
        for(auto e:nums){
            sum+=e;
        }
        return (1+n)*n/2-sum;
    }
};

class Solution {
public:
    int missingNumber(vector<int>& nums) {
        int ret=0;
        for(auto e:nums){
            ret^=e;
        }
        for(int i=0;i<=nums.size();i++){
            ret^=i;
        }
        return ret;
    }
};

leetcode371例题

算法原理讲解：

异或：无进位相加

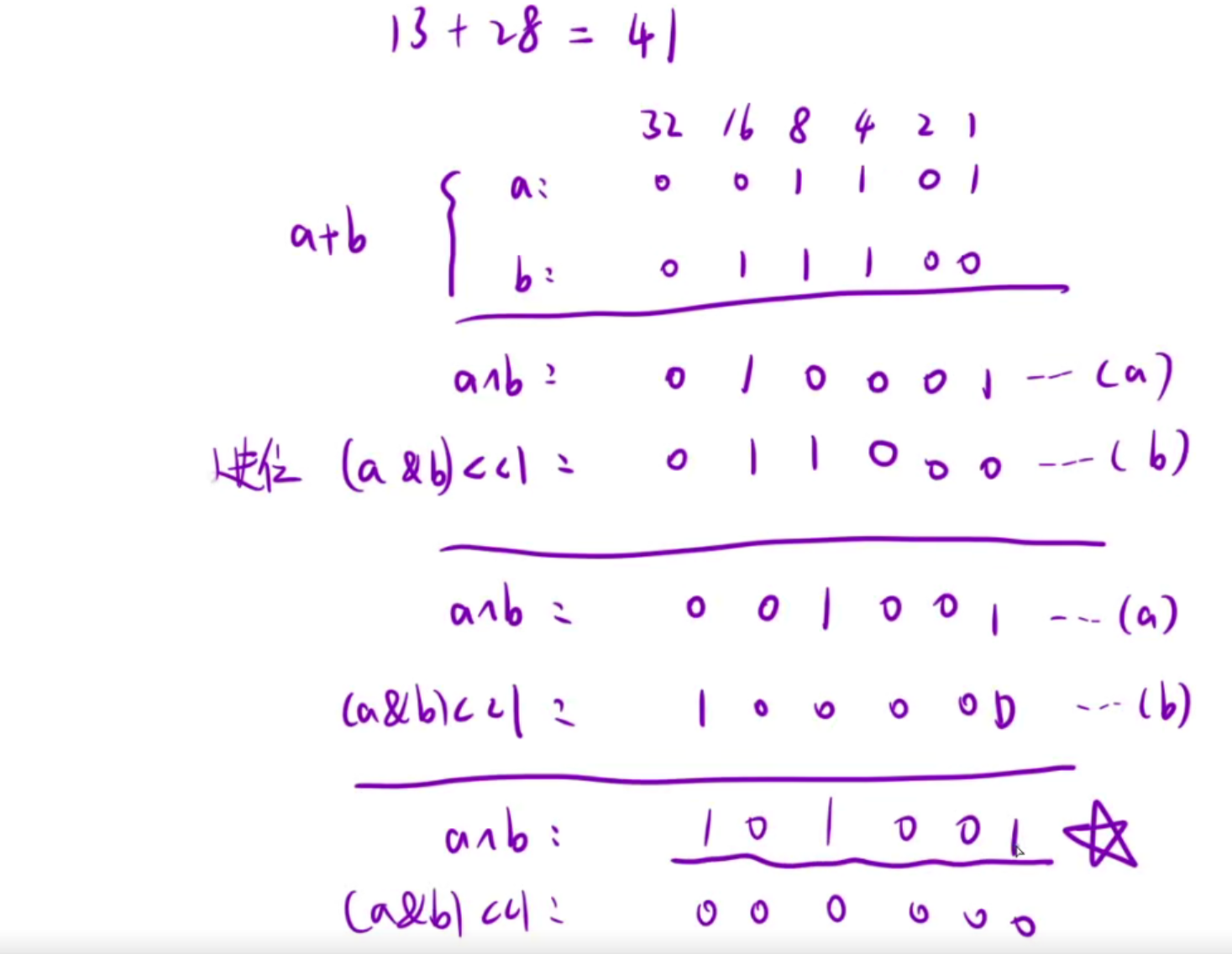
异或之后因为是无进位相加，所以我们需要找到哪一位要进位，进位是1+1才需要，所以我们可以把a和b按位与，按位与完之后还是1就代表是要进位的，但是进位是往高位进，所以要左移，左移完之后又要相加，依次重复这个动作，直到进位为0即可

class Solution {
public:
    int getSum(int a, int b) {
        while(1){
            int tmp=a^b;
            int ret=(a&b)<<1;//这里找进位
            int i;
            for(i=0;i<32;i++){
                //检查ret当中是否有1
                if((ret>>i)&1){
                    a=tmp;
                    b=ret;
                    break;
                }
            }
            if(i==32){
                return tmp;
            }
            
        }
    }
};

leetcode137例题

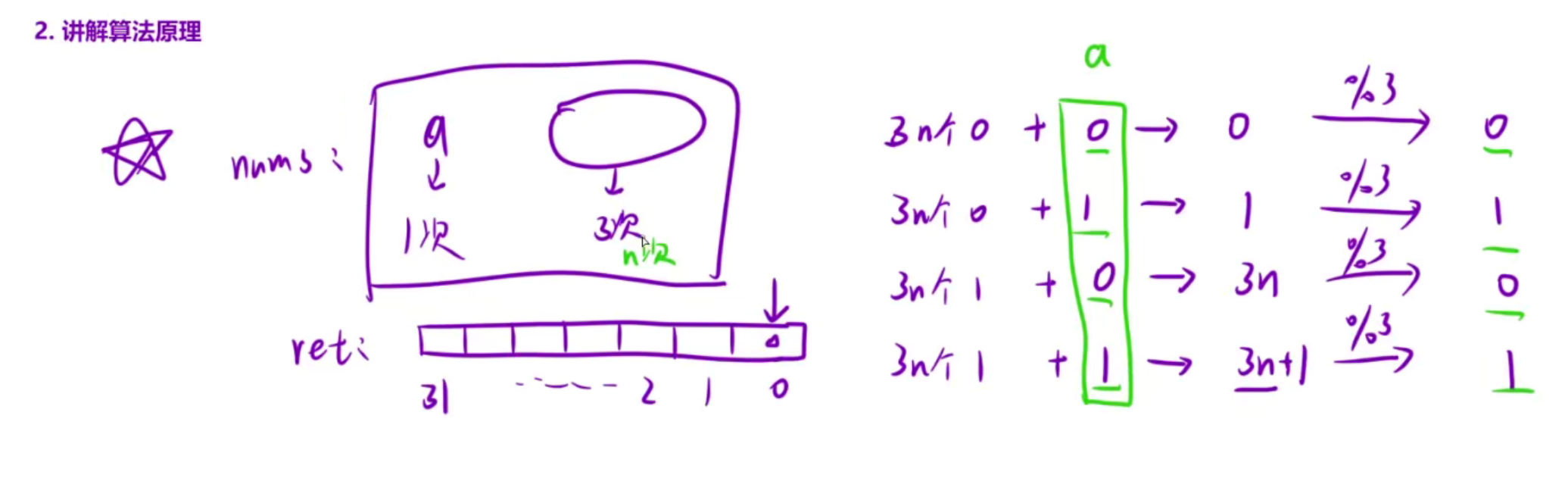
算法原理讲解：意思就是出现3次，你要么3n个0，要么3n个1，所以你对3去模就会得0，所以你统计某一个bit位，如果模了之后=1，说明是目标值做的贡献，如果模了之后=0，说明目标值得这一个比特位为0，没有做贡献

这里可以扩展一下，这类题型目标值出现1次，其他值出现n次，只要模n即可

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int a=0;
        for(int i=0;i<32;i++){
            int sum=0;
            for(int j=0;j<nums.size();j++){
                sum+=(nums[j]>>i)&1;
            }
            if((sum%3)==1){
                a|=1<<i;
            }
        }
        return a;
    }
};

leetcode面试17.19

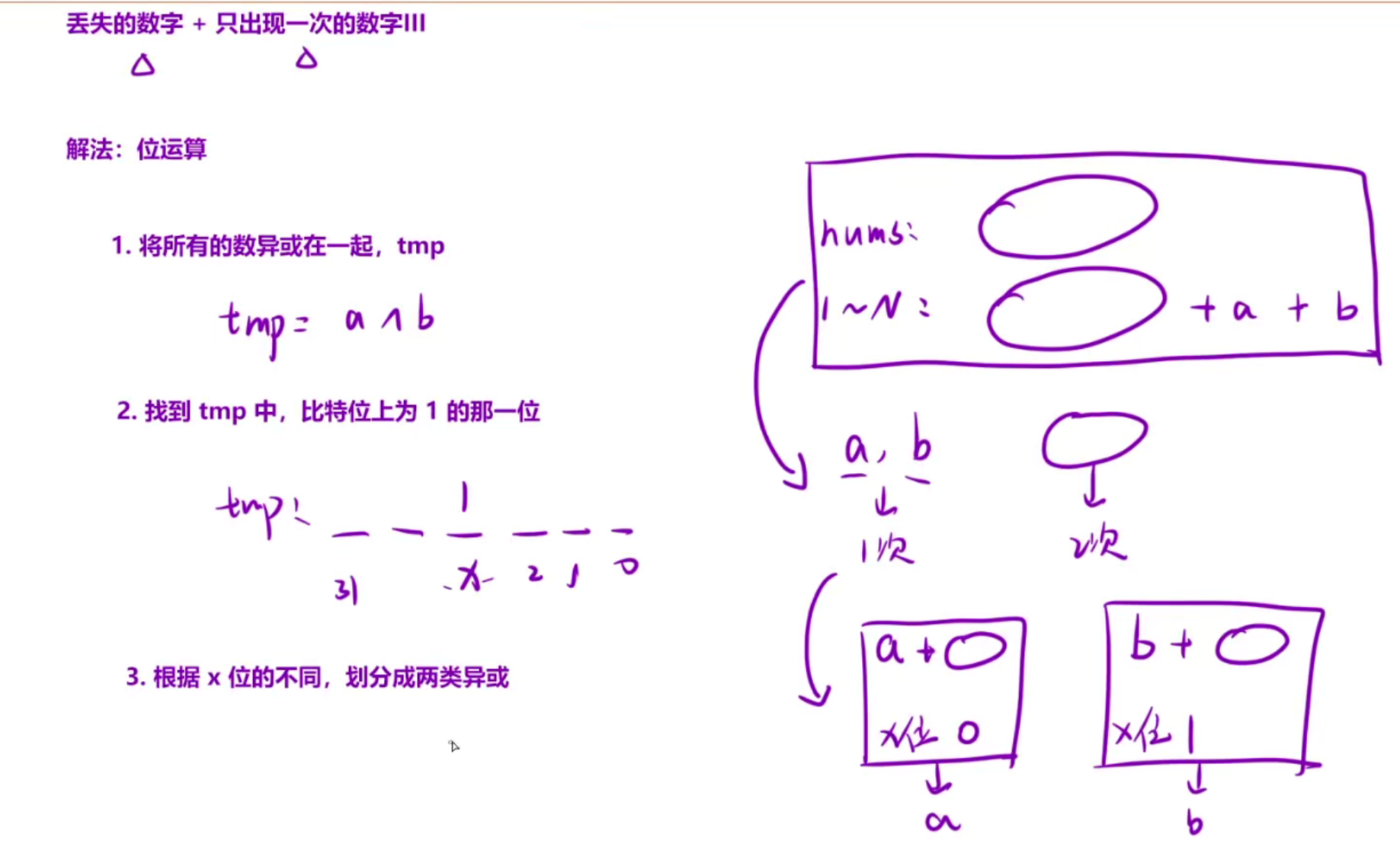
算法原理讲解：第一步先找到丢失的数字，第二步分类，然后转换成只出现一次的数字

class Solution {
public:
    vector<int> missingTwo(vector<int>& nums) {
        //找到丢失的两个数字的异或
        int tmp=0;
        for(auto e:nums){
            tmp^=e;
        }
        for(int i=1;i<=nums.size()+2;i++){
            tmp^=i;
        }
        int a=0;
        int b=0;
        int diff=0;//把相异的位数存入
        while(1){
            if(tmp>>diff&1) break;
            else diff++;
        }

        //分为两类，为1的放到a里，为0的放b
        for(int i=0;i<nums.size();i++){
            if((nums[i]>>diff)&1) a^=nums[i];
            else b^=nums[i];
        }
         for(int i=1;i<=nums.size()+2;i++){
            if((i>>diff)&1) a^=i;
            else b^=i;
        }
        return {a,b};
    }
};