LeetCode #963. Minimum Area Rectangle II

最新推荐文章于 2024-04-14 18:10:44 发布

原创最新推荐文章于 2024-04-14 18:10:44 发布 · 196 阅读

0 ·

CC 4.0 BY-SA版权

LeetCode 专栏收录该内容

625 篇文章

订阅专栏

本文探讨了在二维平面上，由一组给定点形成的任意矩形中，如何找到最小面积的矩形，其边不一定平行于坐标轴。通过具体实例展示了算法的运行过程，包括特殊情况的处理。

题目描述：

Given a set of points in the xy-plane, determine the minimum area of any rectangle formed from these points, with sides not necessarily parallel to the x and y axes.

If there isn't any rectangle, return 0.

Example 1:

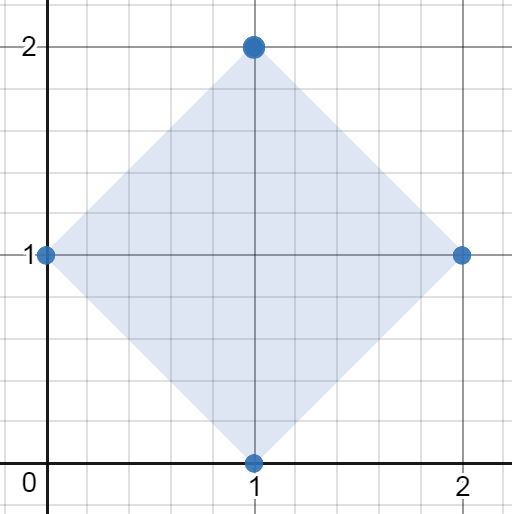
Input: [[1,2],[2,1],[1,0],[0,1]]
Output: 2.00000
Explanation: The minimum area rectangle occurs at [1,2],[2,1],[1,0],[0,1], with an area of 2.

Example 2:

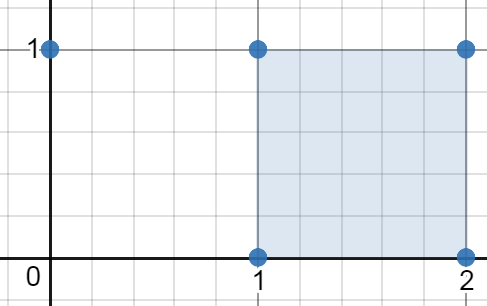
Input: [[0,1],[2,1],[1,1],[1,0],[2,0]]
Output: 1.00000
Explanation: The minimum area rectangle occurs at [1,0],[1,1],[2,1],[2,0], with an area of 1.

Example 3:

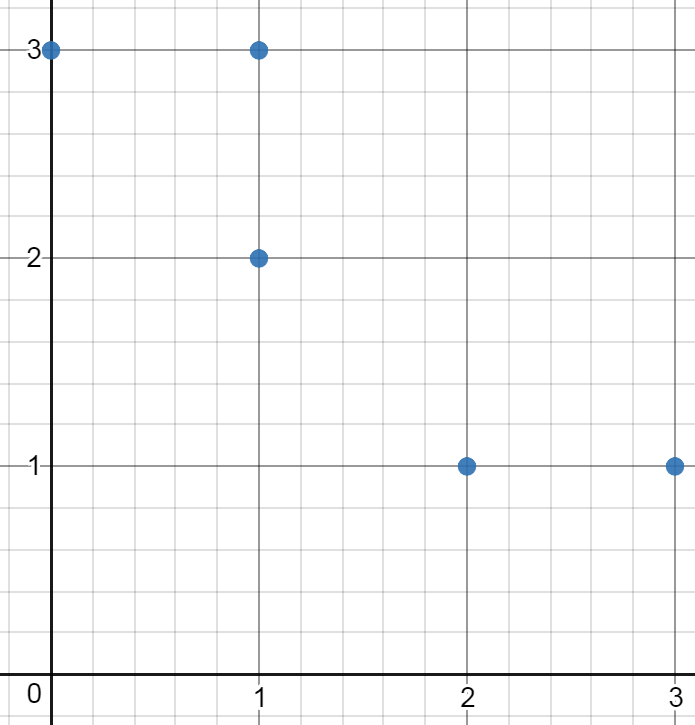
Input: [[0,3],[1,2],[3,1],[1,3],[2,1]]
Output: 0
Explanation: There is no possible rectangle to form from these points.

Example 4:

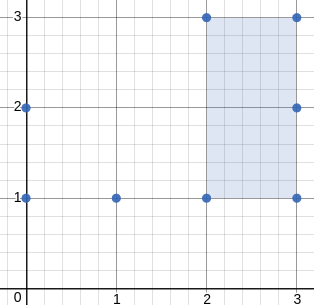
Input: [[3,1],[1,1],[0,1],[2,1],[3,3],[3,2],[0,2],[2,3]]
Output: 2.00000
Explanation: The minimum area rectangle occurs at [2,1],[2,3],[3,3],[3,1], with an area of 2.

Note:

1 <= points.length <= 50
0 <= points[i][0] <= 40000
0 <= points[i][1] <= 40000
All points are distinct.
Answers within 10^-5 of the actual value will be accepted as correct.

class Solution {
public:
    double minAreaFreeRect(vector<vector<int>>& points) {
        int n=points.size();
        for(vector<int>& point:points) s.insert(point[0]*N+point[1]);
        
        double area=DBL_MAX;
        for(int i=0;i<n;i++)
        {
            int x1=points[i][0], y1=points[i][1];
            for(int j=i+1;j<n;j++)
            {
                int x2=points[j][0], y2=points[j][1];
                for(int k=j+1;k<n;k++)
                {
                    int x3=points[k][0], y3=points[k][1];
                    helper(x1,y1,x2,y2,x3,y3,area);
                    helper(x2,y2,x1,y1,x3,y3,area);
                    helper(x3,y3,x1,y1,x2,y2,area);
                }
            }
        }
        if(area==DBL_MAX) return 0;
        else return area;
    }
    
    void helper(int& x1, int& y1, int& x2, int& y2, int& x3, int& y3, double& area)
    {   // 确定p1->p2和p1->p3是否组成一个直角，从而可以得到p4
        if((x1-x2)*(x1-x3)+(y1-y2)*(y1-y3)==0)
        {
            int x4=x2+x3-x1, y4=y2+y3-y1;
            if(s.count(x4*N+y4)) 
                area=min(area,get_dist(x1,y1,x2,y2)*get_dist(x1,y1,x3,y3));
        }
    }
    
    double get_dist(int x1, int y1, int x2, int y2)
    {
        return sqrt((double)(x1-x2)*(x1-x2)+(double)(y1-y2)*(y1-y2));
    }

private:
    unordered_set<int> s;
    int N=40001;
};