常见排序（直接插入、希尔、选择、堆、冒泡、快排、归并、计数）

排序

概念：所谓排序，就是一连串记录，按照其中某个关键字的大小，递增或递减的排列起来的操作

稳定性：假设在待定的排序中，存在多个相同的关键字的记录，若经过排序之后，记录的相对次序不变，即在原来序列中r[i]=r[j],且r[i]在r[j]之前，经过排序后的序列中，r[i]仍然在r[j]之前，则称这种排序算法是稳定的，否则则称为不稳定

• 内部排序：数据元素全部放在内存中的排序
• 外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序

直接插入排序

基本思想：把待排序的记录按其关键码值大小逐个插入到已排好序的序列当中，直到所有记录插入当中为止，得到一个新的有序序列

比如在打扑克牌时将摸到的牌插入到我们排好的牌当中，一张一张摸牌，然后再排好序

void InsertSort(int* a,int n)
{
	for (int i = 1; i < n; i++)
	{   
        //（2）插入值再依次比较
		int end = i-1 ;
		int temp = a[i];
		while (end >= 0)
		{
            //（1）两两比较
			if (a[end] > temp)
			{
				a[end+1] = a[end];
				end--;
			}
			else
			{
				break;
			}
		}
		a[end + 1] = temp;
	}
}

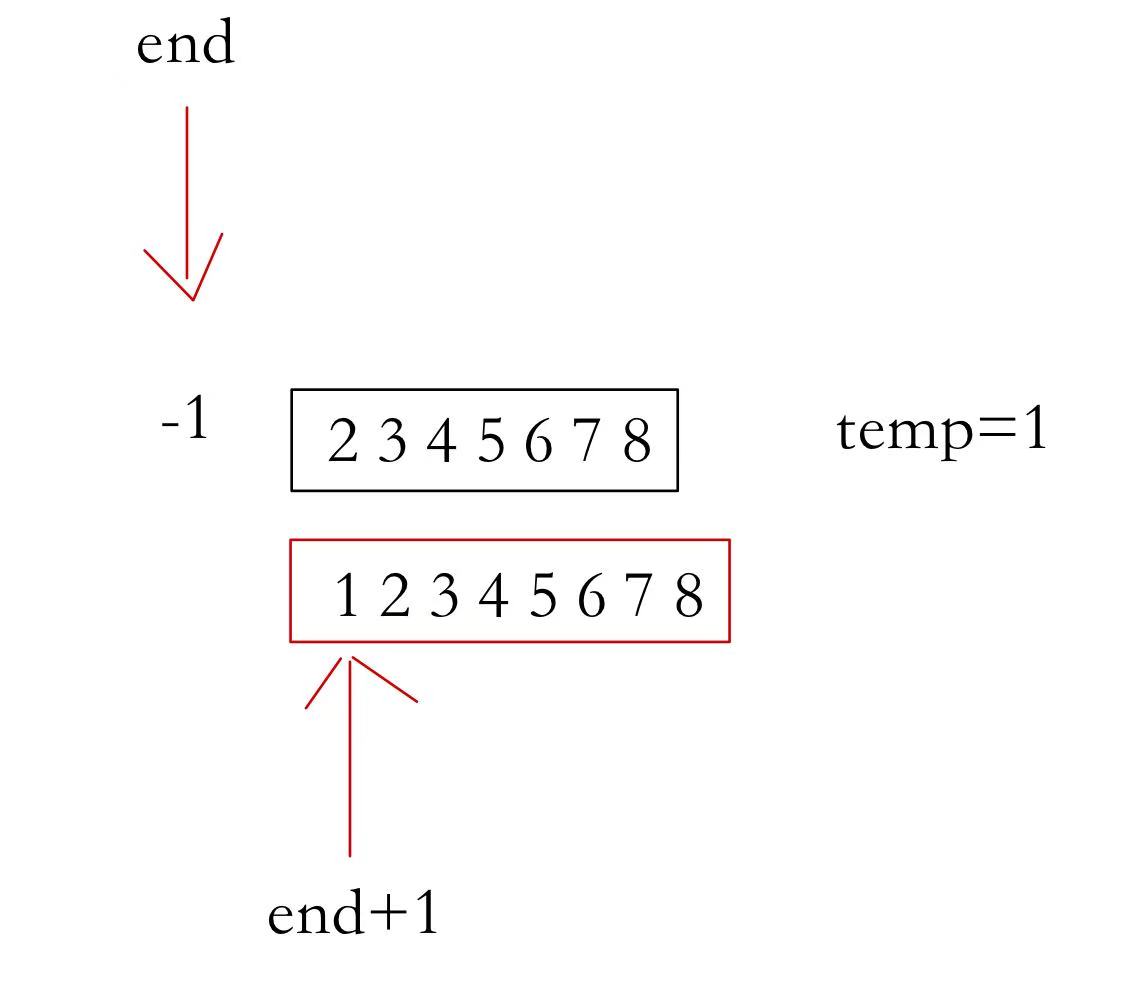
直接插入排序的特性

• 元素越接近有序，直接插入排序算法的时间效率越高
• 时间复杂度O(N^2）
• 空间复杂度O(1）
• 稳定性:稳定

希尔排序

基本思想：把一个数组分为几个组来进行排序，先进行组内的排序，然后缩短步长，当步长等于1的时候，就排好了序

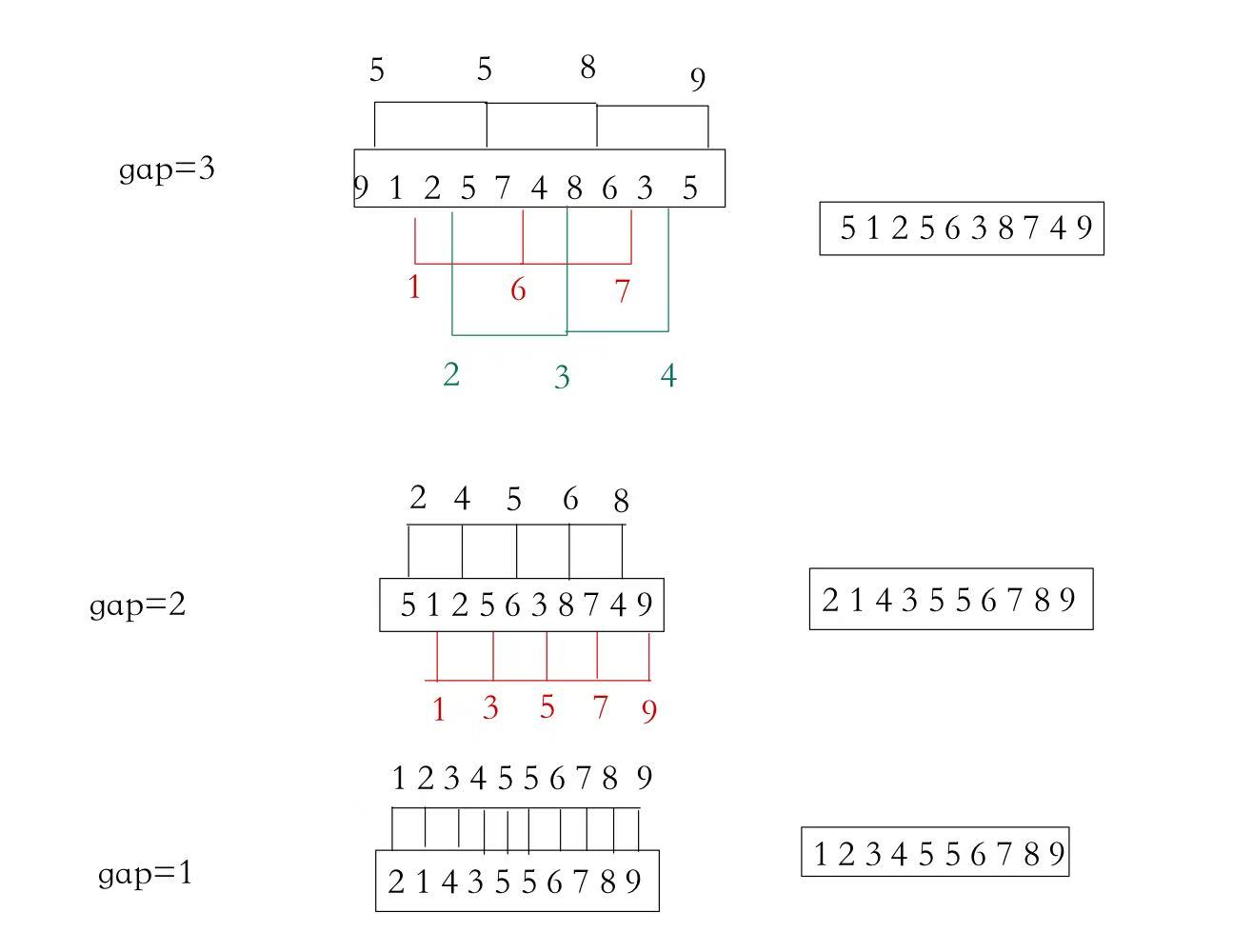
• gap>1 预排序
• gap==1 直接插入排序

void ShellSort(int* a,int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;//保证gap最后能等于1
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int temp = a[end + gap];
			while (end >= 0)
			{
				if (a[end] > temp)
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = temp;
		}
	}
}

希尔排序特性

• 希尔排序是对直接插入排序的优化
• gap>1时是预排序，目的是让数组更加有序，当gap==1时，数组就接近有序了
• 稳定性：不稳定（相同的数据可能分在不同的组）

选择排序

基本思想：每一次从待排序的序列当中选出最小(最大)的一个元素，存放在序列的初始位置，缩减区间，继续挑选最大(最小)的元素,直到全部待排序的数据元素排完

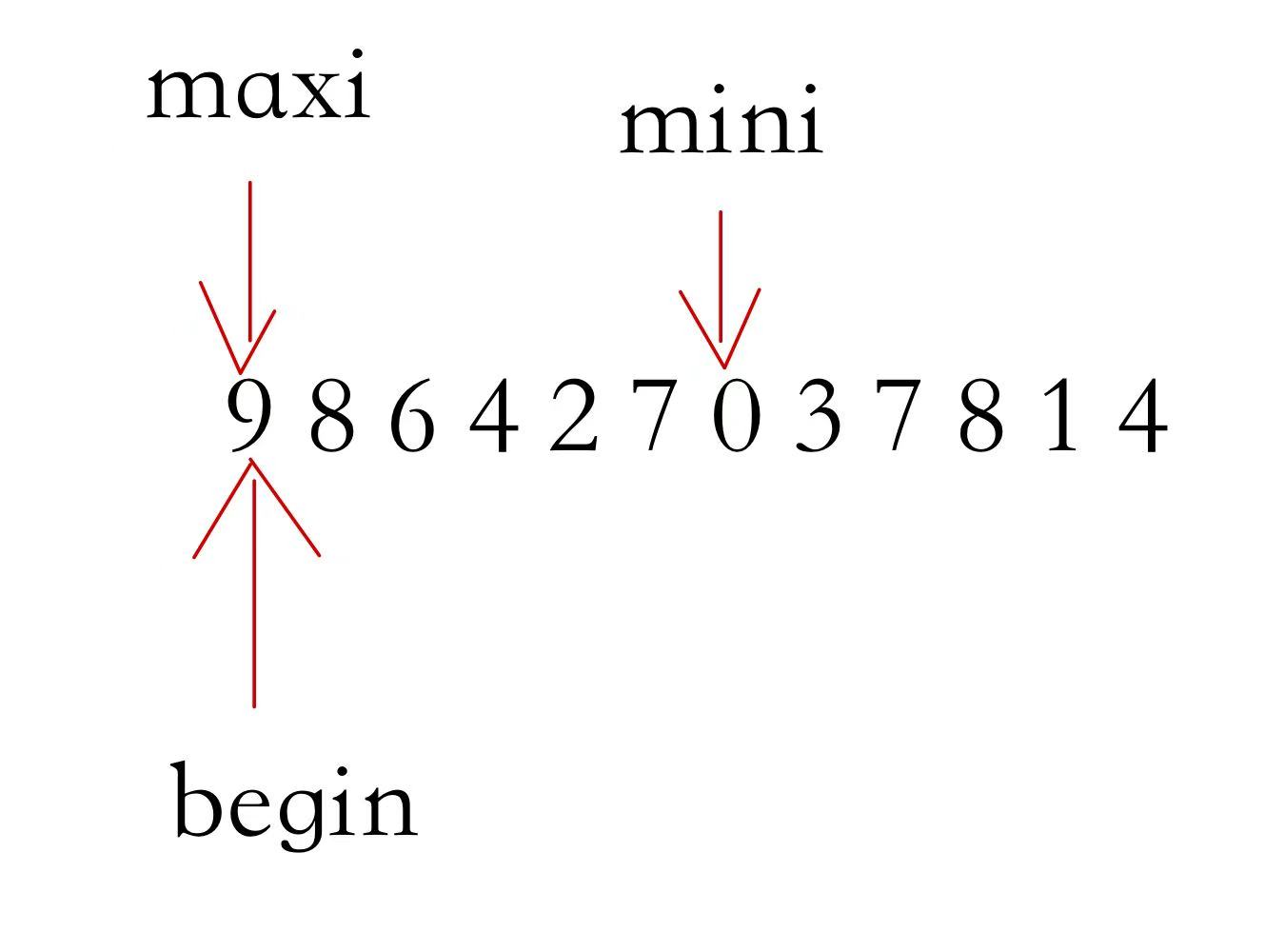
当遇到上面情况时maxi=mini，更改下标否则影响交换

void SelectSort(int* a, int n)
{
	int begin = 0;
	int end = n-1;
	while (begin < end)
	{
		int maxi = begin;
		int mini = begin;
		for (int i = begin; i <=end; i++)
		{
			if (a[i] > a[maxi])
			{
				maxi = i;
			}
			if (a[i] < a[mini])
			{
				mini = i;
			}
		}
		Swap(&a[begin], &a[mini]);
		if (begin == maxi)
		{
			maxi = mini;
		}
		Swap(&a[end], &a[maxi]);
		begin++;
		end--;
	}
}

选择排序特性

• 时间复杂度O(N^2)
• 空间复杂度O(1)
• 稳定性：不稳定（数据交换）

堆排序

堆排序是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。它是 通过堆来进行选择数据。需要注意的是排升序要建大堆，排降序建小堆

基本思想：先建堆，再进行首尾元素交换，再从堆顶向下调整

需要注意的是当最后元素进行交换后，交换后的最后元素不算做堆里面，范围依次递减

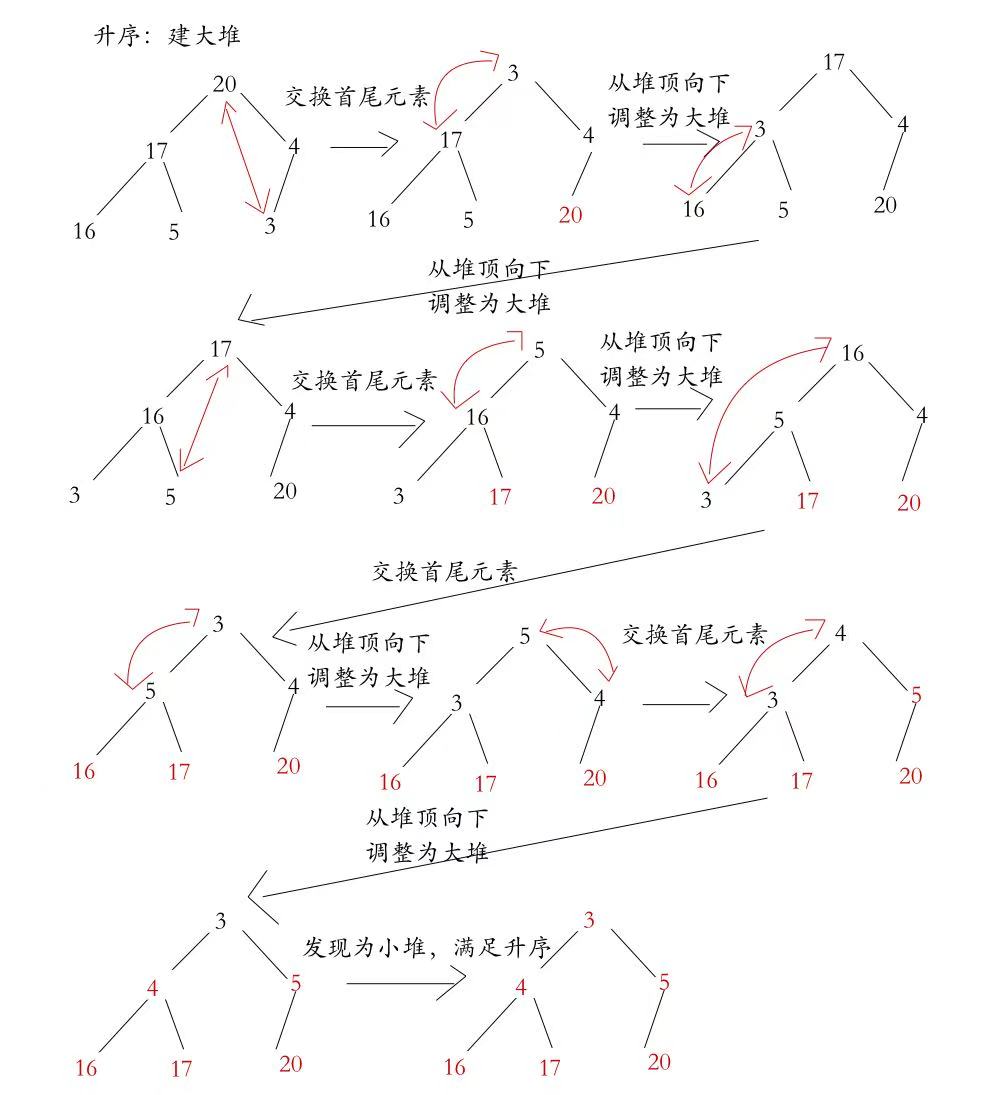
void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child + 1 < n && a[child] < a[child + 1])
		{
			child++;
		}
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapSort(int* a, int n)
{
	//建堆
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, n, i);
	}
	//向下调整
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}

堆排序特性

• 堆排序使用堆来选数，效率更高
• 时间复杂度：O(N*logN）
• 空间复杂度：O(1)
• 稳定性：不稳定

冒泡排序

基本思想：两两比较，将较大的值往后移动，较小的往前移动

void BubbleSort(int* a, int n)
{
	//循环趟数
	for (int i = 0; i < n-1 ; i++)
	{
		//两两比较
		for (int j = 0; j < n-i-1; j++)
		{
			if (a[j] > a[j + 1])
			{
				int temp = a[j];
				a[j] = a[j + 1];
				a[j + 1] = temp;
			}
		}
	}
	
}

冒泡排序特性

• 冒泡排序容易理解
• 时间复杂度O(N^2)
• 空间复杂度O(1)
• 稳定性:稳定

快速排序

基本思想：在数组当中选择某个元素为规定值，将数组划分为两部分，左边部分均小于规定值，右边部分均大于规定值，然后在左右部分当中再次划分，直到所有元素排列好位置

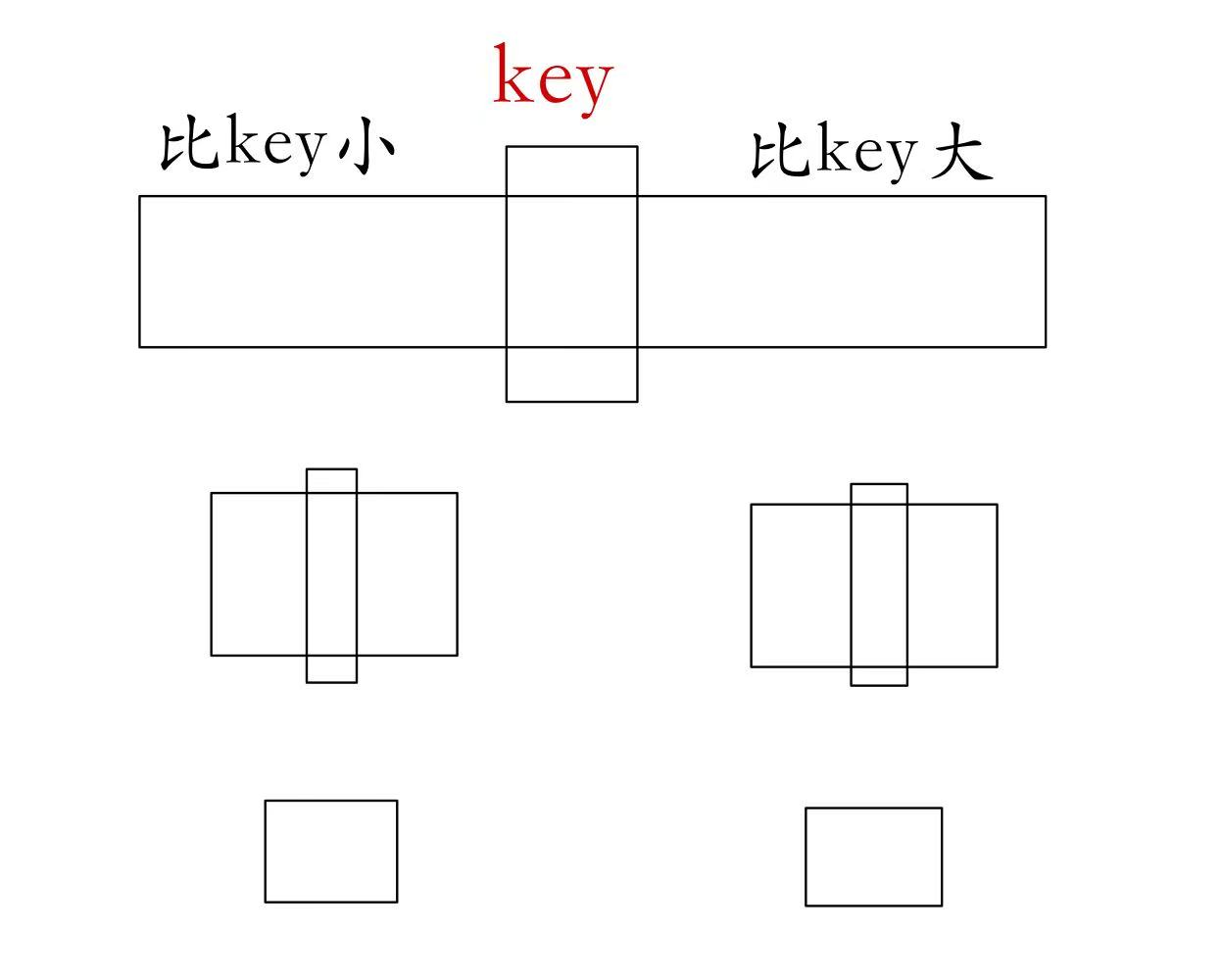
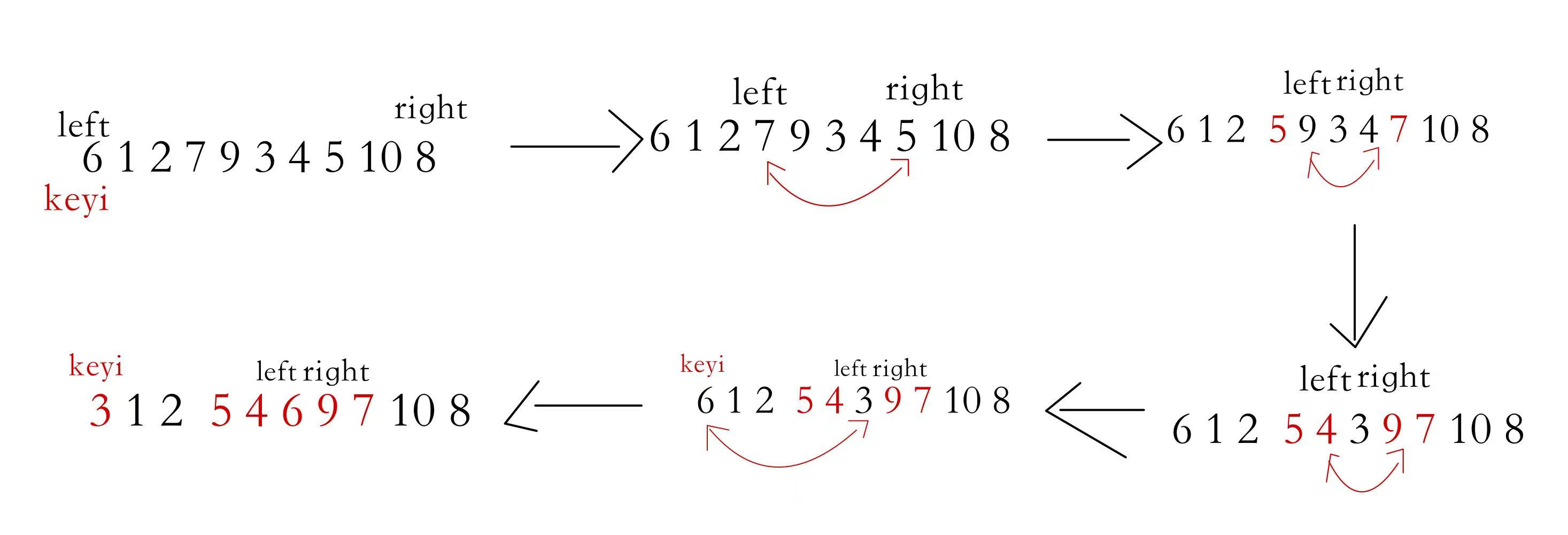
int PartSort(int* a, int left, int right)
{
	int keyi = left;
	while (left < right)
	{
        while (left<right && a[right]>=a[keyi])//左边找大
		{
			right--;
		}
		while (left < right && a[left] <= a[keyi])//右边找小
		{
			left++;
		}
		Swap(&a[left], &a[right]);
	}
	Swap(&a[left], &a[keyi]);
	return left;
}

void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
		return;
	int keyi = PartSort(a, begin, end);
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);
}

快速排序特性

• 快速排序整体的综合性能和使用场景都较好
• 时间复杂度：O(N*logN)
• 空间复杂度：O(logN)
• 稳定性：不稳定

归并排序

基本思想：将一个序列元素分成部分序列元素，再将部分序列元素变成有序，最后将有序的元素合并成一个有序数组

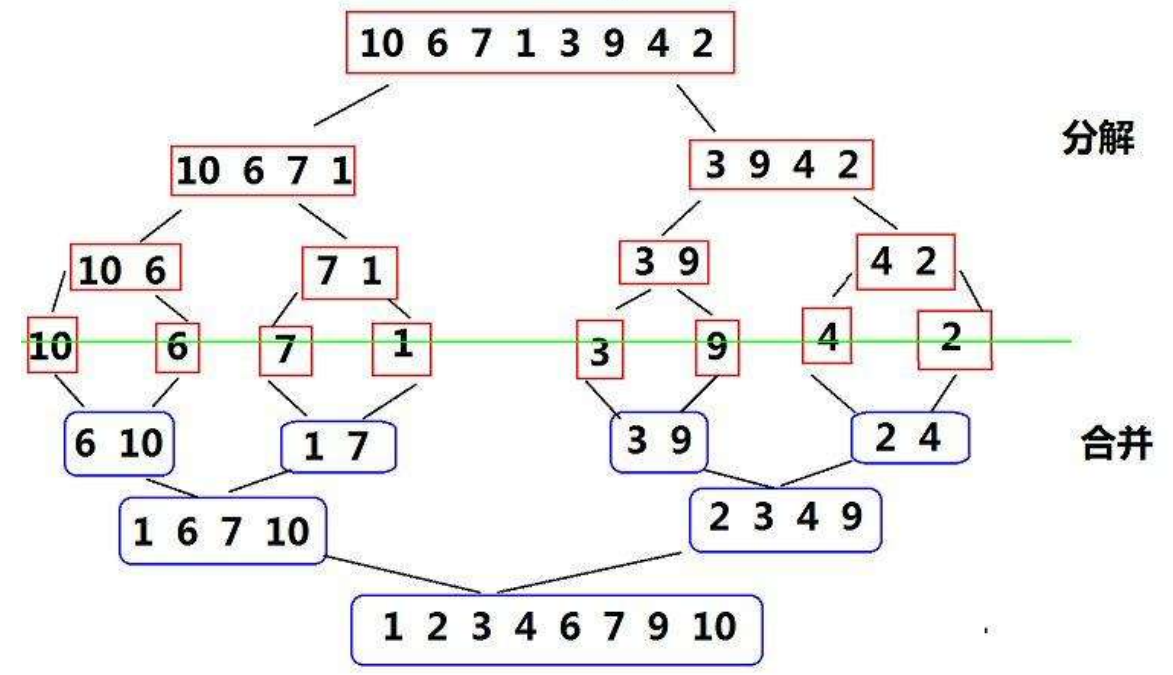
开辟空间时需要注意不是每次都从头开始a + begin temp+begin

开辟空间范围：range=end-begin+1（n=9,end=8,begin=0,range=8-0+1)

void _MergeSort(int* a, int begin, int end,int* temp)
{
	if (begin == end)
		return;
	int midi = (begin + end) / 2;
	_MergeSort(a, begin, midi,temp);
	_MergeSort(a, midi + 1, end,temp);
	int begin1 = begin, end1 = midi;
	int begin2 = midi + 1, end2 = end;
	int i = begin;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			temp[i++] = a[begin1++];
		}
		else
		{
			temp[i++] = a[begin2++];
		}
	}
	while (begin1 <= end1)
	{
		temp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		temp[i++] = a[begin2++];
	}
	memcpy(a + begin, temp+begin, sizeof(int) * (end - begin + 1));

}

void MergeSort(int* a, int n)
{
	int* temp = (int*)malloc(sizeof(int)*n);
	_MergeSort(a, 0, n - 1, temp);
	free(temp);
}

归并排序特性

• 缺点：需要O(N)的空间复杂度
• 时间复杂度：O(N*logN)
• 稳定性:稳定

计数排序

基本思想:统计数组当中每个元素出现的个数，再按照统计次数依次排序

void CountSort(int* a, int n)
{
	int min = a[0], max = a[0];
	for (int i = 0; i < n; i++)
	{
		if (a[i] < min)
		{
			min = a[i];
		}

		if (a[i] > max)
		{
			max = a[i];
		}
	}

	int range = max - min + 1;
	int* countA = (int*)malloc(sizeof(int) * range);
	memset(countA, 0, sizeof(int) * range);

	// 统计次数
	for (int i = 0; i < n; i++)
	{
		countA[a[i] - min]++;
	}

	// 排序
	int k = 0;
	for (int j = 0; j < range; j++)
	{
		while (countA[j]--)
		{
			a[k++] = j + min;
		}
	}
}

计数排序特性

• 依据数据范围，适用于范围集中的数组
• 只能用于整形
• 时间复杂度：O(MAX(N,范围))
• 空间复杂度：O(范围)
• 稳定性：稳定