Logistic回归

Logistic回归常用于二分类问题。当然，也可以用于多分类，多分类可以使用softmax方法进行处理。

二分类

在二分分类问题中，对于某个输入，输出的结果是离散的值。

示例：Cat与Non-Cat，构建一个猫图分类器，即输入一张图片，希望该分类器准确判断出该图片是否为猫图，并输出它的预测结果(猫图1，非猫图0)。

彩色图像以三个独立的矩阵存储在计算机中，分别对应于图像红色、绿色和蓝色三通道信息。这三个矩阵与图像大小相同，例如Cat图像的分辨率为64像素x 64像素，三个矩阵(rgb)分别为64 x 64像素。
在模式识别(Pattern Recognition)及机器学习中，对于处理的各种类型的数据，通常采用一些特征向量来表示。简单地将一张猫图表示为一个特征向量，可以直接把三个矩阵进行拆分重塑，最终形成维数为n_x=64 × 64 × 3 = 12288的特征向量x。

实现这个分类器，需要准备大量的猫图及少量的非猫图，并取其中大部分组成该分类器的训练样本，少部分组成测试样本。将这些样本表示为特征向量的形式，一个样本由一对(x,y)进行表示，其中x为n_x维的特征向量，y是该特征向量的标签(Label)，根据该特征向量表示的是猫图或非猫图，取值为0或1。如果有m个训练样本对，它们将被表示为：
$$(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)})...(x^{(m)},y^{(m)})$$
接着，使用矩阵表示数据，训练集中所有特征向量x⁽¹⁾、x⁽²⁾…x^(m)以及它们的标签y⁽¹⁾、y⁽²⁾…y^(m)分别进行列组合，变成两个矩阵X∈ℝ^{n_x × m}、Y∈ℝ^1×m：
$$X=[x^{(1)},x^{(2)}...x^{(m)}]$$

$$Y=[y^{(1)},y^{(2)}...y^{(m)}]$$

Logistic回归

Logistic回归是一种用于解决监督学习(Supervised Learning)问题的学习算法。进行Logistic回归的目的，是最小化训练数据的标签值与预测值之间的误差。我们接着Cat与Non-Cat的示例，建立猫图分类器的Logistic回归模型。

猫图分类器中，要实现的是：对于给定的特征向量x、标签y，预测该图为猫图的概率ŷ，即：
$$Givex,\hat{y}=P(y=1|x),0\le \hat{y}\le 1$$
我们采用线性拟合的方式，构建ŷ关于x的函数：
$$\begin{gathered} \hat{y}=W^{T}x+b \\ 其中，w\in {\mathbb{R}}^{n_x},b\in \mathbb{R} \end{gathered}$$
由于ŷ为概率值，即ŷ∈[0,1]，而上述线性函数的结果ŷ可能非常大，还可能为负值。所以，我们使用Logistic回归单元来对其值域进行约束。这里以sigmoid函数(σ)为逻辑回归单元， σ函数为：
$$\sigma (z)=\frac{1}{1+e^{-z}}$$
其图像为

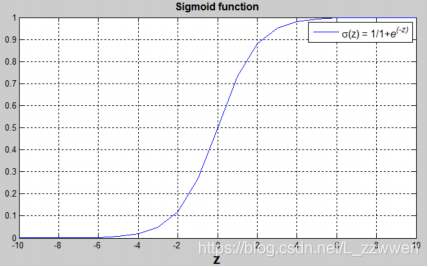
从中可以看出，sigmoid函数具有如下性质：

• 当z趋近于正无穷大时，σ(z)=1;
• 当z趋近于负无穷大时，σ(z)=0;
• 当z=0时，σ(z)=0.5。

所以，可以用sigmoid函数来约束?̂的值域，得到猫图分类器的Logistic回归模型：
$$\hat{y}=\sigma (W^{T}x+b)$$

Cost Function

建立好Logistic回归模型后，接下来要做的就是训练模型参数 w 和 b ，使得y与ŷ尽可能一致。此时，我们需要定义一个损失函数(Loss\Error Function)，用来衡量y与ŷ的差异。

平方误差(Square Loss)就是一种常用的损失函数，其表达式为：

?(ŷ⁽ⁱ⁾ , y⁽ⁱ⁾) =1/2(ŷ⁽ⁱ⁾ − y⁽ⁱ⁾)²

但Logistic回归中，一般不采用平方误差作为损失函数，因为在训练参数过程中，使用这个损失函数将会是非凸的(可能存在很多个局部最优解)，使得后面可能无法使用梯度下降(Gradient Descent)来得到我们想要的最优解。

关于猫图分类器Logistic回归，我们希望能够满足如下条件概率：
$$\begin{gathered} wheny=1,p(y|x)=\hat{y} \\ wheny=0,p(y|x)=1-\hat{y} \end{gathered}$$
合并两个式子可得：
$$p(y|x)={\hat{y}}^y(1-\hat{y}{)}^{1-y}$$
取对数：
$$logp(y|x)=ylog\hat{y}+(1-y)log(1-\hat{y})$$
我们希望p(y|x)的值越大越好，而损失越小越好。将log p(y|x)添上符号(-)，可以作为我们的损失函数，这便是应用很广的交叉熵(Cross Entropy)损失函数：
$$L(\hat{y},y)=-[ylog(\hat{y})+(1-y)log(1-\hat{y})]$$
即：
$$L({\hat{y}}^{(i)},y^{(i)})=-[y^{(i)}log({\hat{y}}^{(i)})+(1-y^{(i)})log(1-{\hat{y}}^{(i)})]$$

• 当y⁽ⁱ⁾=1时，L(ŷ⁽ⁱ⁾ , y⁽ⁱ⁾)=-log(ŷ⁽ⁱ⁾ )，意味着损失越小，ŷ⁽ⁱ⁾ 越接近于1；
• 当y⁽ⁱ⁾=0时，L(ŷ⁽ⁱ⁾ , y⁽ⁱ⁾)=-log(1-ŷ⁽ⁱ⁾ )，意味着损失越小，ŷ⁽ⁱ⁾ 越接近于0；

对m个训练样本整体的成本函数(Cost Function)，可以使用数理统计中的参数估计方法——最大似然估计法(Maximum Likelihood Estimation)。

假设所有训练样本独立同分布，则它们的联合概率为所有样本概率的乘积，得到似然函数为：
$$P(x)=\prod _{i=1}^{m}p(y^{(i)}|x^{(i)})$$
取对数：
$$logP(x)=\sum _{i=1}^{m}logp(y^{(i)}|x^{(i)})=-\sum _{i=1}^{m}L({\hat{y}}^{(i)},y^{(i)})$$
最后得到成本函数j(w , b)= -log P(x)：
$$\begin{gathered} J(w,b)=-logP(x) \\ =>J(w,b)=\frac{1}{m}\sum _{i=1}^{m}L({\hat{y}}^{(i)},y^{(i)}) \\ =>J(w,b)=-\frac{1}{m}\sum _{i=1}^m[(y^{(i)}log({\hat{y}}^{(i)})+(1-y^{(i)})log(1-{\hat{y}}^{(i)})] \end{gathered}$$

梯度下降

训练或学习训练集上的参数 w 和 b ，即要找到参数的最优解，一般采用梯度下降法。所谓的梯度下降，就是从起始点开始，试图每次都沿最陡峭的下降方向下坡，尽可能快地到达最低点即凸函数取得最小值的点，而下坡的方向便是各点上的梯度值。

在空间坐标中以 w，b为轴，画出的损失函数 J 的图像将类似于下图，要找到函数取得最小值的最优参数，先为 w 和 b 赋一个初始值，正如下图的最上面的红点。

对于Logistic回归模型，因为成本函数是凸函数，无论参数的初始值是多少，最后总能到达同一个点或大致相同的点，所以几乎任何初始化方法都有效，于是通常将参数直接初始化为0。

梯度下降法所做的就是：从初始点开始，朝最陡的下坡方向(最快下降的方向)走一步，循环迭代，直到收敛到全局最优解或接近全局最优解。

为了更清楚的理解梯度下降，我们来分析下面这张二维图片

函数的导数(斜率)方向即为梯度方向，下降速度最快。即每经过一次梯度下降，参数?，?即更新为(符合:=表示更新操作)：
$$\begin{gathered} w:=w-\alpha \frac{\partial j(w,b)}{\partial w} \\ b:=b-\alpha \frac{\partial j(w,b)}{\partial b} \end{gathered}$$
α为学习率(learning rate)，是一个超参数。α通常为一个小于1的值，用于控制梯度下降过程中每一次移动的规格大小，好比于下降时每一次迈步的大小。α的不宜太小也不宜过大：太小会使迭代次数增加，容易陷入局部最优解；太大容易错过最优解。

由梯度下降法，训练数据经过多次迭代，就可以求得使成本函数的取得最小值的参数w 和 b，从而建立表现良好Logistic模型，实现我们想要的猫图分类器。

参考资料：
网易云课堂-神经网络和深度学习
文章-Logistic回归