算法-前缀和数组

leetcode 303 区域和检索-数组不可变
1.传统做法

// 传统的做法：
class NumArray {

    private int[] nums;

    public NumArray(int[] nums) {
        this.nums = nums;
    }
    
    // 迭代累加和
    public int sumRange(int left, int right) {
        int res = 0;
        for(int i = left;i<=right;i++) {
            res += nums[i];
        }
        return res;
    }
}

2.前缀和技巧

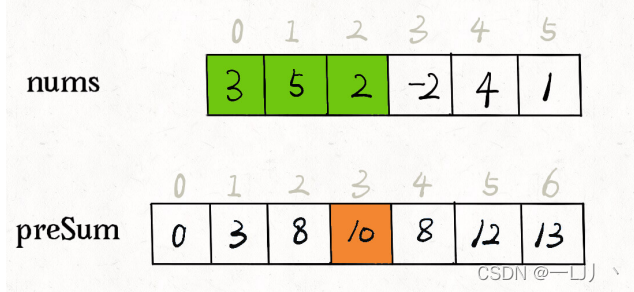
// 前缀和：
class NumArray {

    // 前缀和数组
    private int[] preSum;

    // 构造前缀和
    public NumArray(int[] nums) {
        // 便于计算累加和
        preSum= new int[nums.length + 1];
        preSum[0] = 0;
        for(int i = 1;i < preSum.length;i++) {
            preSum[i] = preSum[i - 1] + nums[i - 1];
        }
    }
    
    // 查询[left, right]累加和
    // 时间复杂度为O(1)
    public int sumRange(int left, int right) {
        return preSum[right + 1] - preSum[left];
    }
}

leetcode 304 二维区域和检索-矩阵不可变

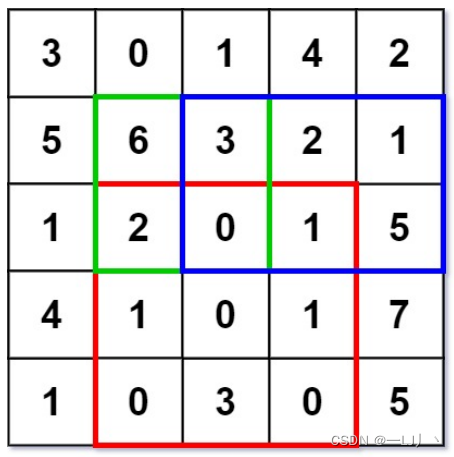
如图中红色的矩阵，即为 [2，1，4，3]，

计算矩阵和的方法为: 大矩阵和[0,0,4,3] - 小矩阵和[0,0,1,3] - 小矩阵和[0,0,4,0] + 小矩阵和[0,0,1,0]。

class NumMatrix {

    // preSum[i][j]记录矩阵[0,0,i,j]的元素和
    private int[][] preSum;

    public NumMatrix(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        if (m == 0 || n == 0) return;
        // 构造前缀和矩阵
        preSum = new int[m + 1][n + 1];
        preSum[0][0] = 0;
        preSum[1][0] = 0;
        preSum[0][1] = 0;
        for(int i = 1;i <= m;i++) {
            for(int j = 1;j <= n;j++) {
                // 计算每个矩阵[0,0,i,j]的元素和
                preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] - preSum[i - 1][j - 1] 
                    + matrix[i - 1][j - 1];
            }
        }
    }
    
    // 计算子矩阵[row1,col1,row2,col2]的元素和
    public int sumRegion(int row1, int col1, int row2, int col2) {
        // 四个相邻矩阵运算获得
        return preSum[row2 + 1][col2 + 1] - preSum[row1][col2 + 1] - preSum[row2 + 1][col1]
            + preSum[row1][col1];
    }
}

leetcode 560 和为 K 的子数组

class Solution {
    public int subarraySum(int[] nums, int k) {
        int n = nums.length;
        // 构造前缀和
        int[] preSum = new int[n + 1];
        preSum[0] = 0;
        for(int i = 1;i <= n;i++){
            preSum[i] = preSum[i - 1] + nums[i - 1];
        }
        int res = 0;
        for(int i = 1;i <= n; i++){
            for(int j = 0;j < i;j++){
                if(preSum[i] - preSum[j] == k) res++;
            }
        }
        return res;
    }
}

优化：

直接记录下有几个 preSum[j] 和 preSum[i] - k 相等，直接更新结果，就避免了内层 的 for 循环。我们可以用哈希表，在记录前缀和的同时记录该前缀和出现的次数。

class Solution {
    public int subarraySum(int[] nums, int k) {
        int length = nums.length;
        // map 前缀和 -> 该前缀和出现的次数
        Map<Integer, Integer> preSum = new HashMap<>();
        // base case
        preSum.put(0, 1);

        int res = 0;
        int sum0_i = 0;
        for (int i = 0; i < length; i++) {
            // 前缀和 nums[0...i]
            sum0_i += nums[i];
            // 这是我们想找的前缀和 nums[0...j]
            int sum0_j = sum0_i - k;
            // 包含前缀和 nums[0...j] 则更新 res
            if (preSum.containsKey(sum0_j)) {
                res += preSum.get(sum0_j);
            }
            // 把前缀和 nums[0...i] 加入并记录次数
            preSum.put(sum0_i, preSum.getOrDefault(sum0_i, 0) + 1);
        }
        return res;
    }
}