- Semi-supervised Learning
- Unsupervised Learning :Word Embedding
十二、Semi-supervised Learning(半监督学习)
1、介绍
Supervised learning :{(xr,y^r)}r=1R\begin{Bmatrix}
(x^r,\hat{y}^r)
\end{Bmatrix}^R_{r = 1}{(xr,y^r)}r=1R,其中xrx^rxr :image,y^r\hat{y}^ry^r:class labels;
Supervised learning有一大堆training data,组成是一个function的input和output;
Semi-Supervised learning :{(xr,y^r)}r=1R\begin{Bmatrix}
(x^r,\hat{y}^r)
\end{Bmatrix}^R_{r = 1}{(xr,y^r)}r=1R,{xu}u=RR+U\begin{Bmatrix}
x^u
\end{Bmatrix}^{R+U}_{u = R}{xu}u=RR+U
Semi-Supervised learning :(1)在labeled data上有另一组unlabeled的data,即xux^uxu,只有function的input,没有output;(2)一般,希望unlabeled的数量远大于labeled的数量,即U>>R;(3)Semi-Supervised learning 可以分成两种:Transductive learning(导入学习)、Inductive learning(归纳学习),在做Transductive learning时unlabeled data 就是testing data,在做时Inductive learningunlabeled data 不是testing data。
为什么要做Semi-Supervised learning ?
收集数据容易,但是搜集labeled的数据不容易
2、Semi-Supervised learning for Generative Model
Supervised Generative Model:labeled training examples xr∈C1,C2x^r\in C_1,C_2xr∈C1,C2,已知这些data分别属于class 1 还是class 2,会去估测prior probability P(Ci)P(C_i)P(Ci)以及class-dependent probability P(x∣Ci)P(x|C_i)P(x∣Ci);假设每个class的分布都是Gaussian distribution:

有了这些数据P(C1),P(C2),μ1,μ2,ΣP(C_1),P(C_2),\mu^1,\mu^2,\SigmaP(C1),P(C2),μ1,μ2,Σ,就可以求一个新的data属于C1C_1C1还是C2C_2C2的概率,就可以做Classification,决定boundary的位置:

但是如果给了unlabeled data,就会影响这个决定。假设下图绿色的点为unlabeled data的话,它们分布的形状也会发生改变:

Semi-Supervised Generative Model:首先初始化一组参数
θ={P(C1),P(C2),μ1,μ2,Σ}\theta = \begin{Bmatrix}
P(C_1),P(C_2),\mu^1, \mu^2,\Sigma
\end{Bmatrix}θ={P(C1),P(C2),μ1,μ2,Σ};
(1)第一步,估算每一笔unlabeled data属于class 1的posterior probability Pθ(C1∣xu)P_\theta (C_1| x^u)Pθ(C1∣xu);(取决于model θ\thetaθ)
(2)第二步,update model
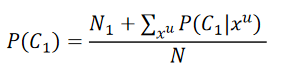
其中,N表示所有的example,N1N_1N1表示被标注为C1C_1C1的example;
计算μ1\mu^1μ1,在之前的基础上加上unlabeled data用概率计算的期望值:

(3)根据第二步得到的新的model,返回到第一步,update第一步几率;算法最终收敛,但初始化会影响结果。

3、Low-density Separation Assumption(低密度分离假设)
(非黑即白)
Self-training:有一些labeled data = {(xr,y^r)}r=1R\begin{Bmatrix}
(x^r,\hat{y}^r)
\end{Bmatrix}^R_{r = 1}{(xr,y^r)}r=1R,有一些unlabeled data ={xu}u=lR+U\begin{Bmatrix}
x^u
\end{Bmatrix}^{R+U}_{u = l}{xu}u=lR+U;
(1)先从labeled dat去train一个model f∗f^\astf∗;
(2)根据f∗f^\astf∗去label你的unlabeled data;
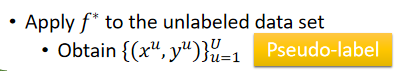
pseudo-label(伪标签);
(3)接下来从你的unlabeled data set里拿出一些data,加到labeled data set中,甚至可以给每一笔unlabeled data加上weight;
(4)回到第一步,用更新的数据去train model f∗f^\astf∗;(这个在Regression没有用)
Self-training与Semi-supervised learning for generative model,它们唯一的差别是Self-training用的是hard label(强制一笔training data一定是属于某个类),Semi-supervised learning for generative model用的是soft label(根据posterior probability有一部分属于class 1,一部分属于class 2);
那么hard label和soft label哪个更好?
假设现在考虑neural network:θ∗\theta^\astθ∗(network参数)from labelled data,现在有一组unlabelled data xux^uxu,通过network把它分成两类,0.7的几率属于class 1 ,0.3的几率属于class 2;
如果是hard label直接label成class 1,所以xux^uxu的target就变成[10]\begin{bmatrix}
1\\
0
\end{bmatrix}[10];
如果是soft label,就是70%属于class ,30%属于class 2,所以xux^uxu的target就变成[0.70.3]\begin{bmatrix}
0.7\\
0.3
\end{bmatrix}[0.70.3];

在neural network中soft label不会有用。
以上方法有个进阶版:Entropy-based Regularization(基于熵的正则化):
如果你使用neural network,你的output是一个distribution,这个distribution一定要很集中,假设现在做5个分离,在class 1上的几率很大,在其它class上的几率很小,这种distribution是好的:
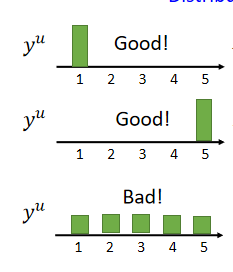
用数字的方法评估好坏:entropy of yuy^uyu–评估这个distribution有多集中,公式(其中,ymuy^u_mymu为对每一个class的几率):
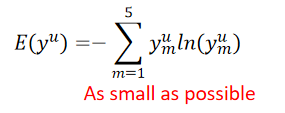
以上三种情况的entropy为:
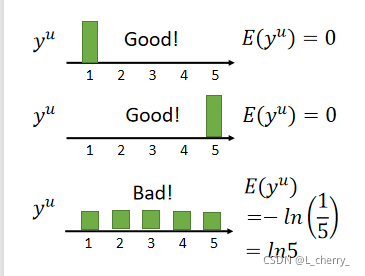
根据这个假设可以设计Loss Function(希望找一组参数在labeled data上的model output离正确的model output距离越近越好;加上每一笔unlabelled data的output distribution的entropy):

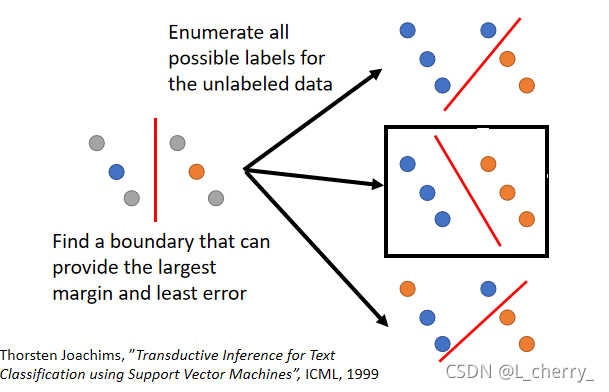
其它Semi-supervised 的方式:Semi-supervised SVM:
4、Smoothness Assumption(光滑性假设)
(近朱者赤,近墨者黑)
Assumption:xxx的分布是不平均的,如果x1x^1x1和x2x^2x2在一个high density的region很接近的话,x1x^1x1的label y^1\hat{y}^1y^1和x2x^2x2的label y^1\hat{y}^1y^1他们也会很像。
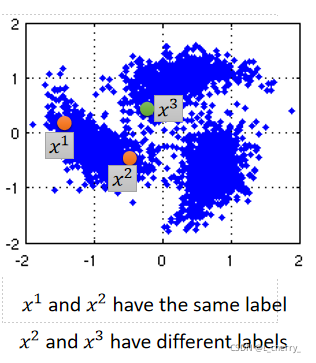
实现Smoothness Assumption的方法:
(1)Cluster and then label:
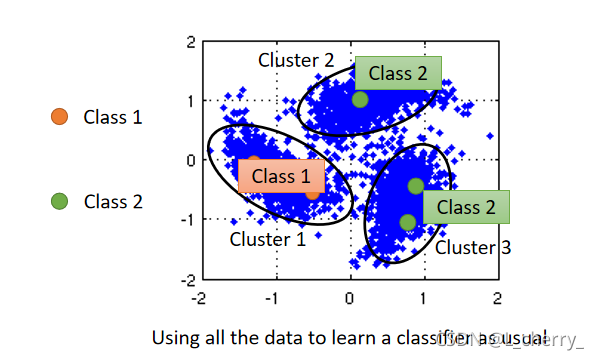
把data distribution分成三个cluster,可以看出cluster 1 中橙色的labeled data最多,所以cluster 1中的所有data都为class 1,以此类推…这个方法不一定有用。
(2)Graph-based Approach
使用Graph Structure表达high density path:represented the data points as a graph,如果有两个点它们在这个graph上是相连的,就是同一个class,反之,就算实际距离不算太远,也不是同一class。

怎么想办法建立这个Graph?
(1)定义两个点之间的相似度s(xi,xj)s(x^i,x^j)s(xi,xj)
(2)建立graph,add edge:
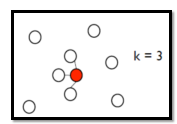
- K Nearest Neighbor:现有一大堆data,data之间可有算出相似度,若k = 3,每一个point都跟它最近的(相似度最高)三个点相连;
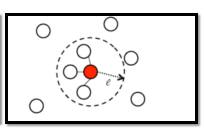
- e-Neighborhood:每一点只有跟它相似度超过e的才会被连起来:
(3)可以给edge一些weight,和两个点之间的相似度s(xi,xj)s(x^i,x^j)s(xi,xj)成正比的,怎么定义相似度呢?建议使用Gaussian Radial Basis Function(高斯径向基函数):
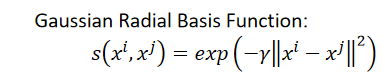
怎么使用这个graph:
假如在一个graph上我们有一些labeled data,那些跟它们相连的data point和它们属于同一类的几率也会上升,每一笔data都会影响它的邻居,并且这个class是会传递的,会传递到没有相邻的点:

怎么定量地使用这个graph:
在graph 的structure上,定义label的smoothness,代表着这个label有多符合Smoothness Assumption。
举例:以下两个graph都有4个data point,两点之间的数字代表edge weight,给每个data不同的label,谁比较smooth?
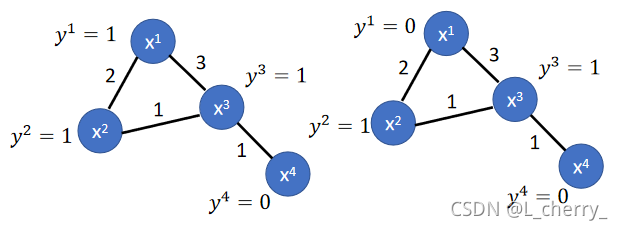
定义表达smooth的公式:

得到左边的smooth值为0.5,右边为3,越小表示越smooth。
现在改变一下以上的公式:
yyy: (R+U)-dim vector(包括labeled data和unlabelled data)
y=[⋯yi⋯yj⋯]Ty = \begin{bmatrix}
\cdots y^i\cdots y^j\cdots
\end{bmatrix}^Ty=[⋯yi⋯yj⋯]T
那么smooth公式变为:

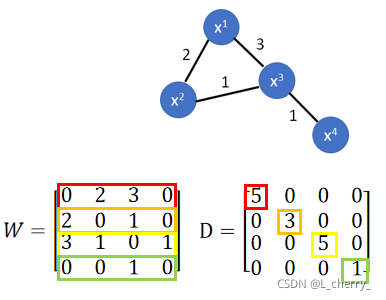
这个L:(R+U) x (R+U) matrix(Graph Laplacian)
L=D−WL = D - WL=D−W
其中 WWW为graph中edge weight建立的matrix;DDD为把W的每一行合起来放到对角线上;例如:
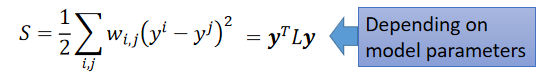
以上求smooth的公式,取决于network 参数,把graph 的information考虑到neural network的training的时候,要做的事情就是在原来的loss function中加一项,比如在cross entropy后面加上smooth的值乘上你想要调的参数:

计算smooth不一定是在output,比如deep neural network,可以放在任何地方,可以把某个hidden layer接出来,再乘上一些别的transform,再去smooth,也可以每一个hidden layer的output都要是smooth的:
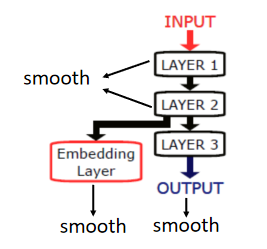
5、Better Representation
(化繁为简)
在Unsupervised Learning部分讲解。
十三、Unsupervised Learning :Word Embedding(无监督学习:单词嵌入)
Embedding在数学上表示一个maping, f: X -> Y, 也就是一个function,其中该函数是injective(就是我们所说的单射函数,每个Y只有唯一的X对应,反之亦然)和structure-preserving (结构保存,比如在X所属的空间上X1 < X2,那么映射后在Y所属空间上同理 Y1 < Y2)。那么对于word embedding,就是将单词word映射到另外一个空间,其中这个映射具有injective和structure-preserving的特点。通俗的翻译可以认为是单词嵌入,就是把X所属空间的单词映射为到Y空间的多维向量,那么该多维向量相当于嵌入到Y所属空间中,一个萝卜一个坑。word embedding,就是找到一个映射或者函数,生成在一个新的空间上的表达,该表达就是word representation。
用一个vector来表示一个word:
(1)一般是用1-of-N Encoding:每一个word用一个vector来表示,vector的dimension就是这个世界上word可能有的数目,每一个word对应到其中一维:

(2)辨别同一种类的word:Word Class,把不同的word但是同样性质的word把它们分成一群一群的,然后用那个word 所属的class来表示这个word:

(3)但是这也是不够的,会少一些information,需要Word Embedding:把每一个word都放到一个high dimension的空间上(这个dimension远比1-of-N Encoding的dimension要低),同样类似语义的词汇在这个图上是比较接近的,每一个dimension可能都有它特别的含义:

1、怎么做Word Embedding?
让machine阅读大量的文章,他就会知道每一个词汇的embedding feature vector长什么样子。
Generating Word Vector是unsupervised的:
learn一个neural network,你的input是一个词汇,你的output就是这个词汇的word embedding vector,training data是大量的文字,我们不知道每一个 word embedding vector长什么样子,找的function就是单向的,只知道输入,不知道输出。
了解一个词汇就要看这个词汇的context,每一个词汇的含义可能根据上下文得到,那么如何通过这个找出word embedding vector?有两个不同体系的做法:
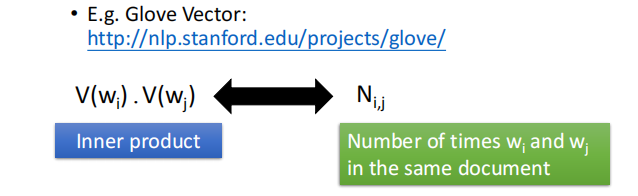
(1)Count based(基于计数)
如果现在有两个词汇wiw_iwi和wjw_jwj,它们常常在同一个文章中出现,那么它们的word emdedding vector V(wi)V(w_i)V(wi)和V(wj)V(w_j)V(wj)会很接近;
这种方法代表性的例子叫做 Glove Vector:假设我们知道V(wi)V(w_i)V(wi)和V(wj)V(w_j)V(wj),我们可以计算它们的inner product(内积),假设Ni,jN_{i,j}Ni,j是wiw_iwi和wjw_jwj出现在同一个document的次数,希望 V(wi)V(w_i)V(wi)和V(wj)V(w_j)V(wj)的内积和Ni,jN_{i,j}Ni,j越接近越好:
(2)Perdiction based(基于预测的)
learn一个neural network,它用来做prediction,假设给一个sentence,给予前一个word,使用neural network 预测下一个可能出现的word;
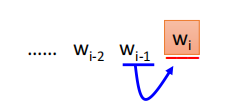
每一个word都用1-of-N encoding表示成一个feature vector,如果要做prediction这件事,就得learn一个neural network,它的input就是wi−1w_{i-1}wi−1的1-of-encoding 的feature vector,它的output就是下一个word wiw_iwi是某一个word 的几率,也就说这个neural network的output的dimension就是的lexicon(词汇表) size。假设现在世界上有10w个word,这个output就是10w维,每一维代表某一个word是下一维的几率。input和output都是lexicon size。
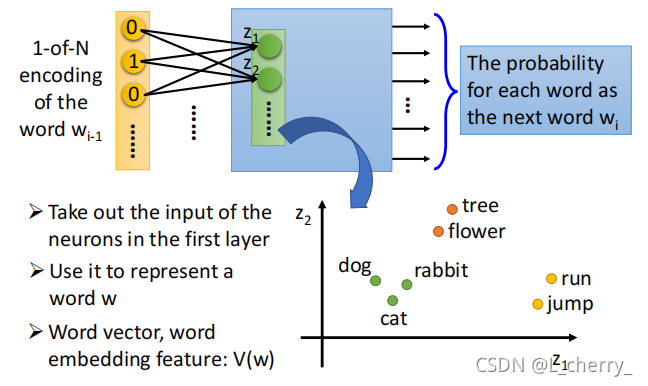
假设这个就是multi-layer 的perceptron的deep neural network,把input feature vector丢进去的时候,通过很多hidden layer,就会得到output,接下来把第一个hidden layer的input拿出来(这里用ziz_izi表示),用z1z_1z1代表一个词汇 www,当作这个word emdedding,就可以得到这个现象:
2、Prediction-based
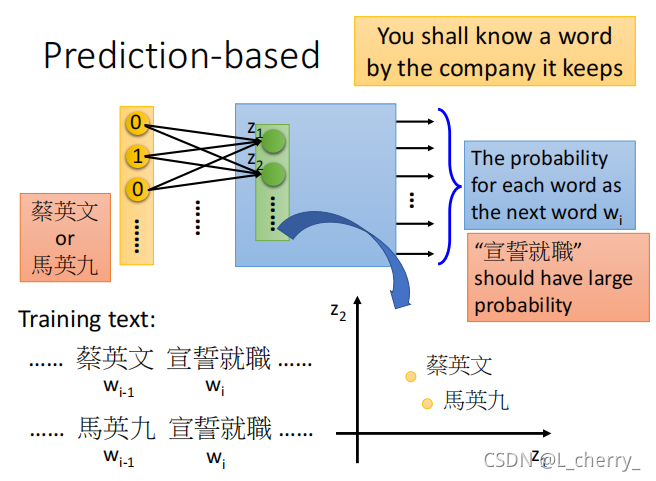
Prediction-based的方法是怎么体现我们说的可以根据一个词汇的上下文来了解一个词汇的含义这件事?
假设training data里面有一个文章告诉我们:
…张三使用计算机…(那么“张三“就是wi−1w_{i-1}wi−1,”使用计算机“就是wiw_{i}wi)
…李四使用计算机…(那么”李四“就是wi−1w_{i-1}wi−1,”使用计算机“就是wiw_{i}wi)
那么在训练这个predication model时不管是input ”张三” 还是 “李四”,都希望learn出来的结果是“使用计算机”的几率比较大;为了让最后output一样,就必须让中间的hidden layer必须学到这两个不同的词汇通过参数的转换后把它们对应到同样的空间,在input进入hidden layer之前必须把它们对应到接近的空间,这样把它们最后output时才能有同样的几率。
所以,当我们learn 一个prediction model时考虑word context这个事情就自动地被考虑到这个prediction model中,因此把这个prediction model 的第一个hidden layer拿出来,我们就可以得到我们想要找的这种word embedding的特性。
只用wi−1w_{i-1}wi−1预测wiw_{i}wi显得太弱,这里可以拓展,learn的是input前面两个词汇,predict input的下一个词汇,这样可以轻易把这个model 拓展到N个词汇,input通常至少10个词汇,这里input两个word当作例子,那么就可以轻易地把这个model拓展到10个词汇:
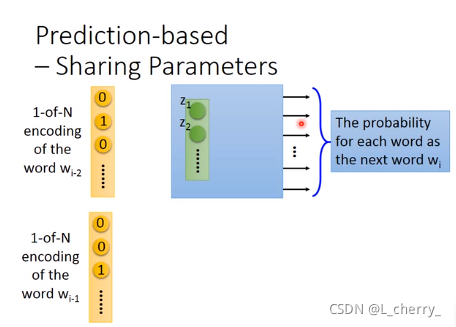
这里要注意的是,本来如果是一般的neural network,就把input wi−2w_{i-2}wi−2和wi−1w_{i-1}wi−1的1-of-N encoding vector接在一起变成一个很长的vector,直接丢到neural network里面当作input就可以,但是实际上,wi−2w_{i-2}wi−2的第一个dimension和第一个hidden layer它们之间连的weight,与,wi−1w_{i-1}wi−1的第一个dimension和第一个hidden layer它们之间连的weight必须是一样的,其它dimension同理:
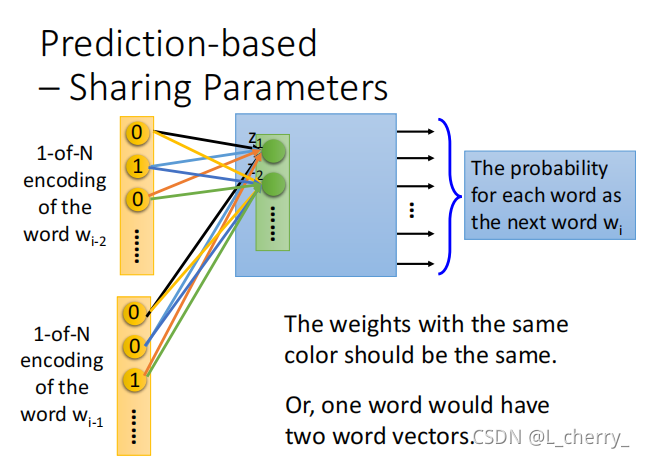
这样做的理由:
(1)如果不这样做,你把同一个word放在wi−2w_{i-2}wi−2的位置,和放在wi−1w_{i-1}wi−1的位置,通过这个transform后得到的embedding就会不一样;
(2)可以减少参数量。
现在假设这个wi−2w_{i-2}wi−2的1-of-N encoding就是xi−2x_{i-2}xi−2,wi−1w_{i-1}wi−1的1-of-N encoding就是xi−1x_{i-1}xi−1,它们的长度都是∣V∣|V|∣V∣(绝对值),这个hidden layer的写成vector zzz,它的长度为∣Z∣|Z|∣Z∣:
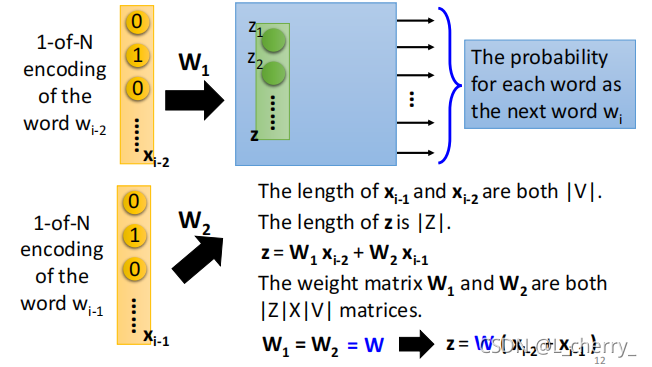
那么zzz和xi−1x_{i-1}xi−1、xi−2x_{i-2}xi−2的关系为:z=W1xi−2+W2xi−1z = W_1x_{i-2}+W_2x_{i-1}z=W1xi−2+W2xi−1,其中W1W_1W1和W2W_2W2都是∣z∣x∣v∣|z|x|v|∣z∣x∣v∣ matrices,这里强制让W1=W2=WW_1 = W_2 =WW1=W2=W,即z=W(xi−2+xi−1)z = W(x_{i-2}+x_{i-1})z=W(xi−2+xi−1)。
如果要得到一个word vector时,只要把一个word 的1-of-N encoding乘上这个WWW,那就可以得到那个word 的word embedding。
如何让Wi=Wj=WW_i = W_j =WWi=Wj=W?
首先给WiW_iWi和WjW_jWj一样的初始值,接下来计算WiW_iWi对cost function的偏微分,更新WiW_iWi,Wj同理W_j同理Wj同理:

如果WjW_jWj和WjW_jWj不一样,它们update之后也不一样,解决方法是在WiW_iWi的update公式中再减掉WjW_jWj对CCC的偏微分,WjW_jWj同理:
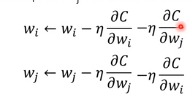
这样就可以保证WiW_iWi和WjW_jWj它们在训练的过程中永远都是一样的。
3、Prediction-based-- Training
首先收集一大堆文字的data:

让neural network input “潮水”、“退了”,让output target是 ”就“,希望output和output target的cross entropy是minimizing cross entropy;接下来让neural network input “退了”、“就”,让output target是 ”知道“; input “就”、“知道”,让output target是 ”谁“…
4、Prediction-based-- various architecture
Prediction-based model有很多变形,如Continuous bag of word (CBOW) model、Skip-gram。
(1)Continuous bag of word (CBOW) model(连续字袋模型)
拿某个词汇的context去predict中间的词汇,用wi−1w_{i-1}wi−1和wi+1w_{i+1}wi+1去predict wiw_iwi:
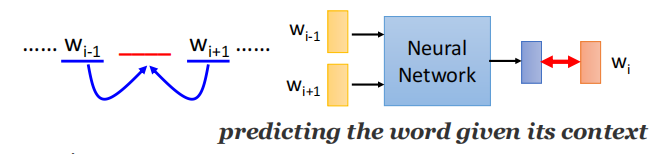
(2)Skip-gram
拿中间的词汇去predict接下来的context,用wiw_{i}wi去predict wi−1w_{i-1}wi−1和wi+1w_{i+1}wi+1:

5、Word Embedding
(1)如果把同样类型的word vector摆在一起,比如把某个国家和它的首都摆在一起,它们之间有某种固定的关系;或者说把动词的三态摆在一起,他们之间会有某种固定的关系成为三角形:

(2)把两个word vector两两相减,project到一个 Q Dimension Space上,如果这两个word vector代表的事物是包含关系,它们减掉之后的结果与其它同情况的word vector的差值结果是类似的:
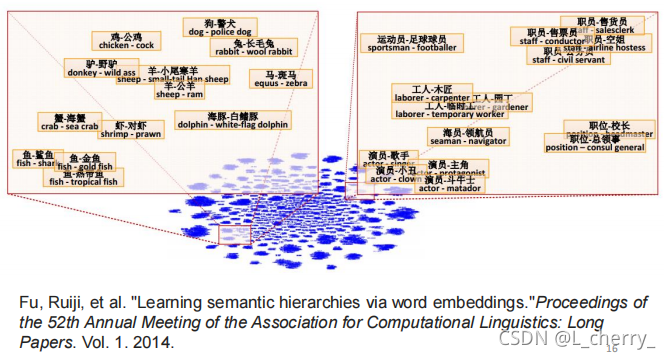
根据这一概念可以做一些简单的推论:
a.Characteristics

b.Solving analogies
如果有人问Rome:Italy = Berlin:?(罗马之于意大利=柏林之于什么)。这个答案Germany的vector会很接近于:

计算上式,找到word www最接近V(w)V(w)V(w)。
(3)word vector还可以把不同语言的word vector拉在一起:比如有一组中文的corpus,和一组英文的corpus,分别去training一组word vector,会发现中英文的word vector没有任何关系,如果corpus里面没有中英文的句子混杂在一起,machine就无法判断中文词汇和英文词汇的关系。
假如,你已经事先知道某几个中文词汇和几个英文词汇是对应在一起的,先得到一组中文的vector,再得到一组英文的vector,接下来可以再learn一个model,它把中文对应英文的词汇把它们project到space上的同一个点。
如果做transform后,接下来有新的中文词汇和新的英文词汇,都可以用同样的projection把它们project到同样的space上。
6、Multi-domain Embedding
对影像做embedding:现在已经找到一组word vector,比如dog、horse、cat、auto的vector它们分布在空间上,如下图:
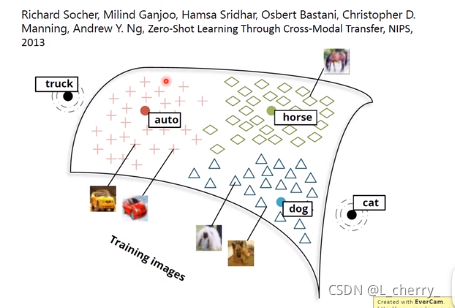
接下来learn一个model,input是一张image,output是word vector一样dimension的vector,希望狗的vector就散布在狗的周围,马的vector就散布在马的周围…假设有些image已知是属于哪一类的,可以把它们project它们所对应的word vector附近。假设你现在input一张image(猫,但是此时未知),把它project到这个space上,发现它可能就出现在猫的附近,machine这个时候就能知道这张image是猫。
一般在做影像分类的时候,machine很难处理新增加的它没有看过的东西,但是使用Multi-domain Embedding这个方法可以解决这个问题。
7、Document Embedding
把document变成一个vector:把document变成一个Bag-of-word,使用auto-encoder就可以learn出这个document的semantic embedding,但这样是不够的,因为词汇的顺序代表不同的含义。
方法:

本文是对blibli上李宏毅机器学习2020的总结,如有侵权会立马删除。





 这篇博客介绍了半监督学习的概念,解释了为什么需要半监督学习,特别是在数据标注困难的情况下。接着,文章讨论了无监督学习中的单词嵌入,描述了如何通过神经网络和预测模型学习单词的表示。文章还提到了基于计数和预测的两种方法,如GloVe和基于预测的模型,并展示了这些方法如何捕获词汇的上下文信息以生成词向量。
这篇博客介绍了半监督学习的概念,解释了为什么需要半监督学习,特别是在数据标注困难的情况下。接着,文章讨论了无监督学习中的单词嵌入,描述了如何通过神经网络和预测模型学习单词的表示。文章还提到了基于计数和预测的两种方法,如GloVe和基于预测的模型,并展示了这些方法如何捕获词汇的上下文信息以生成词向量。
















 17万+
17万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








